从“经验操作”到“学会推理”
2021-09-13张彦伍王金发
张彦伍 王金发


《数学课程标准》指出,合情的推理就是“从已有的事实出发,凭借经验和直觉,通过归纳和类比等推断某些结果”。教学过程中,教师引导学生根据已有的学习经历和生活经验,通过动手操作、观察,从多角度验证和推理出知识的规律,是培养学生具有良好学习能力的方法,有助于学生对知识的深度理解和提升学生探究能力。笔者现以人教版四年级下册第五单元《四边形内角和》的教学为例,谈谈如何教授学生从已有的经验进行操作,学会推理。
一、课例展示
《四边形内角和》是学生在学习了三角形的内角和的基础上展开教学的。笔者课前对学生的学习情况做了一个小测试。
《四边形内角和》课前探究
问题1:四边形的内角和是( )度。
问题2:你是如何验证四边形内角和的度数?
从学生对问题的反馈来看,问题1回答的正确率在90.5%。这说明四边形内角和的认知,大部分学生已经知道;问题2(如图1)从回答情况来看,大部分学生的验证主要表现在两个方面:第一,学生探究的方法较为单一;第二,学生从特殊的四边形中获得了四边形内角和的度数。据此,笔者将教学的重心“要知道什么?”转为“怎么知道的?”教学中,重点将引导学生利用已有的学习经验,借助三角形内角和这一结论,推理出四边形的内角和,并将方法延伸。根据前测情况,教学实录如下:
(一)温故引新,激发探究
课件出示一个三角形。
师:上一节课我们学习了三角形的内角和,知道了三角形的内角和是多少 度?
生:180°。
师:我们是如何发现并验证三角形内角和是180°?
生1:通过量一量,折一折。
生2:还有拼一拼,把三角形的三个内角拼成了一个平角。
生3:我们还从特殊的直角三角形中得到了三角形内角和的度数。
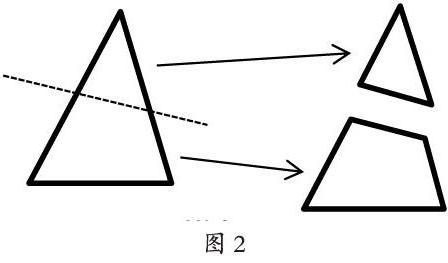
師:真棒!看来同学们对上一节课的知识掌握的很好,还能够记得从特殊中寻找一般的规律。同学们请看,像这样将三角形减去一个角(如图2),将会得到两个什么图形呢?
生:一个三角形,一个四边形。
师:这个小三角形还有内角和吗?
生:有,还是180°。
师:那这个四边形它有内角和吗?是多少呢?这节课我们就一起来研究四边形的内角和。
(二)迁移经验,操作实践
师:同学们,有没有那么一种四边形,一看到它,就能知道它的内角和?
生:有。
师:它是什么样的四边形呢?
生1:我知道它是长方形,因为它的四个角都是直角,90°×4=360°。
生2:正方形也有4个直角,每个角是90°,它的内角和是90°×4=360°
师:真不错,这样说来四边形的内角和估计也应该是360°。但是,这只是我们的一种假设,因为长方形和正方形是一种特殊的四边形。是所有四边形的每一个内角都是90°吗?
生:不是。
师:同学们,特殊四边形并不能完全说明一般四边形内角和这一规律,显然我们还得研究一般四边形的内角和到底是多少度?
师:同学们,你能借助研究三角形内角和学习的方法和经验,也研究一下一般四边形的内角和吗?现在小组合作,一起尝试研究吧。
(小组合作学习后汇报)
小组1:我们小组用量角器测量了4个角的度数,再把它们加在一起,计算的结果是75°+105°+75°+105°=360°。
小组2:我们组用的是折一折的方法(如图3),经过折叠后,4个内角拼成了一个周角,周角的度数是360°,所以这个四边形的内角和是360°。
小组3:我们组是把这个四边形的四个角剪了下来,(如图4)然后把它们拼在一起,也拼成了一个周角,所以这个四边形的内角和是360°。
师:还有其它方法吗?
小组4:我们组是直接把四边形撕成四份,把四个内角拼在一起也是一个周角,所以我们小组得出四边形内角和也是360°。(如图5)
师:以上小组的汇报非常精彩,都能运用研究三角形内角和的方法和经验,来研究四边形的内角和,虽然方法不同,但都得出了四边形内角和的度数是360°。
(三)突破经验,尝试推理
师:同学们,在刚才的研究中,大家先从特殊的四边形开始猜想,接着运用了量一量、折一折和拼一拼的方法进行了验证,这些都是上一节课学习的经验。我们也熟知三角形的内角和是180°这一结论,也就是说只要有一个三角形,它的内角和就一定是多少度?
生:180°。
师:同学们,你能运用这个结论来研究一下四边形的内角和吗?想一想,能在这个四边形中找到三角形吗?
(学生思考)
师:你可以用笔连一连,画一画。
(学生先独立完成,再小组交流)
师:刚才老师发现,很多同学都已经找到了三角形,请同学们一起看下他们是怎样连的。(投影出示)(如图6)
师:从这两种连线方法我们可以看出,它们都把四边形分成了两个三角形,
一个三角形的内角和是180°,两个就是180°×2=360°,说明四边形的内角和是360°。
师:从连线的方法上看,这个四边形只要连接不相邻的两个点,就可以连出三角形。我们也可以沿着连线的地方剪开两个三角形,两个三角形的内角和加在一起同样是360°。你们同意吗?
生:同意。
师:但老师有疑问了,四边形原来只有4个内角,这样剪开后变成6个角,这是怎么回事呢?你能解释现在的6个角就是原来的4个角吗?
生:(学生板演并说明)(如图7)这两个角原本是四边形的内角,剪开后分别是三角形的内角了,现在把它拼回来,还是四边形原来的内角。
