正交FeH5结构、力学和电子性质的第一性原理研究*
2021-09-13李世娜
权 浩,李世娜
(1. 山西大学 理论物理研究所, 太原 030006; 2. 量子光学与光量子器件国家重点实验室, 太原 030006)
0 引言
随着实验技术的不断提高以及理论计算科学的不断成熟,越来越多的铁氢化合物被发现。近年来,Pépin等在压强分别为67 和86 GPa下,合成了FeH2和FeH3[9]。随后的实验中,他们对Fe与H2进行激光加热,保持T=1500K,获取了加热前后1分钟的XRD衍射图样,发现在130~140 GPa存在有新的衍射峰[10],进一步分析发现该衍射峰为富氢化物FeH5,其结构为I4/mmm的四方晶系,并利用ABINIT程序包确定了H原子的具体位置。Kvashnin[11]利用USPEX程序包得到了具有稳定结构的FeH、FeH3、I4/mmm-FeH5和Fe3H5等新型铁氢化合物。Zarifi[12]等分别采用进化算法的XTALOPT和粒子群优化算法的CALYPSO程序包在压强为150 、200和300 GPa对FeHX(X=5~8)进行结构搜索,获取了FeHX(X=5~8)的多个新结构。引起我们注意的是在P=300 GPa时出现了一个与I4/mmm-FeH5相几乎等焓的正交Cmca-FeH5相,通过声子谱的分析发现其在相应压强下是动力学稳定的。近期,Sagatova等[13]采用AIRSS随机搜索的方法获得了I4/mmm-FeH5和Cmca-FeH5这两种结构,并利用晶格动力学准谐近似法得到了它们的P-T相图。
目前,大多数的研究集中在I4/mmm-FeH5的相关性质上[11-14],反观对Cmca-FeH5的结构、电子和力学等各种性质的研究少之又少。通过对材料在高压条件下弹性性质的研究可以更深入的分析材料的力学稳定性、声波传播和弹性各向异性等信息。以密度泛函理论为基础的第一性原理模拟方法是分析材料高压相关性质的有效理论工具。因此本文采用第一性原理计算方法对高压下Cmca-FeH5的晶格常数、键长等结构参数,能带结构和电子态密度等相关电子特性进行模拟,并采用能量-应变和应力-应变两种方法对Cmca-FeH5的多晶弹性模量、德拜温度等弹性力学性质进行对比分析。本文的研究工作能够为之后实验和理论上获得Cmca-FeH5的相关物理性质提供理论参考。
1 计算参数及方法
运用密度泛函理论为背景的VASP[15]第一性原理软件包计算了Cmca-FeH5在压强为300 GPa时的结构、力学和结构电子特性。利用广义梯度近似[16]下的Perdew-Burke-Ernzerhof(PBE)泛函来处理体系的交换关联势,并选择投影缀加平面波法(PAW)[17]来描述电子与离子间的作用。Cmca-FeH5中Fe的3d74s1和H的1s1作为价电子。经过一系列的测试,当P= 300 GPa时,平面波截断能定为600 eV,布里渊区K点网格密度为2π*0.015 nm-1。采用全优化法对Cmca-FeH5进行结构弛豫,设置的力和能量的收敛标准分别为0.2 eV/nm、10-5eV。
另外,实验上材料的单晶弹性常数Cij较难测量。本文从理论上采用能量-应变(E-S)[18]和应力-应变(S-S)[19-20]两种方法对Cmca-FeH5的弹性常数进行了模拟计算,进而分析了其弹性力学性质。这两种方法被广泛的应用于各种材料的弹性常数计算中[21-23],其中E-S方法是对晶格施加不同的应变δ,得到相应的能量。高压下吉布斯自由能能量差ΔG与δ之间呈二次线性关系(胡克定律)[18]:
(1)
本文研究的Cmca-FeH5属正交晶系,需选取9种应变δ来获得其9个单晶独立弹性常数Cij,即C11、C12、C13、C22、C23、C33、C44、C55、和C66。δ与Cij之间的关系与文献[19]中采用的相同。而S-S方法[24]只对晶格进行六次有限应变后利用最小二乘法便能够确定弹性常数,其包括离子形变和离子弛豫作用。
2 结果与讨论
2.1 晶体结构分析
本文基于Zarifi等搜索到的300 GPa下FeH5的正交Cmca结构[12],进行了结构优化与性质的计算分析。在300 GPa下,该相比I4/mmm相的焓值低0.02 meV/atom,与文献[12]中得到的结果(两相之差低于1 meV/atom)吻合地较好。表1中详细列举了弛豫后Cmca-FeH5的晶格常数。弛豫后的晶格常数与文献[12]的对比吻合较好。本文所运用的计算方法以及所有参数的设置是可行的。正交Cmca-FeH5原胞中包含有4个分子式(Z=4)。Cmca-FeH5的结构图及其在ac、bc和ab平面的投影图如图1所示。其中,各原子的Wyckoff占据位置分别为:Fe_8d(0.604,0,0);H1_16g(0.810,0.282,0.284)、H2_8d(0.263,0,0)、H3_8d(0.089,0,0)和蓝色球H4_8f(0,0.248,0.75)。如图2(a)所示,Fe原子周围有13个H原子,其中H2一个,H1、H3和H4各四个,该结构存在两个八面体结构分别由Fe-H1-H3-H4和Fe-H4组成。本文所研究的正交Cmca-FeH5与四方I4/mmm-FeH5(如图2(b))的不同之处在于H1-H1-H1之间的键角分别为90.46°和90.00°。Cmca-FeH5与I4/mmm-FeH5相比,H-H之间发生了扭曲,这与Zarifi等[12]得出的研究结论相一致。另外,表1还给出了Cmca-FeH5中Fe-Fe、Fe-H、H-H之间的键长信息。Fe-Fe、Fe-H和H-H之间的最近邻键长分别为0.2257、0.1433和0.1241 nm,与文献[12]中计算报道的最近邻Fe-Fe键长(0.2238 nm)、Fe-H键长(0.1424 nm)和H-H键长(0.1236 nm)相一致。对比发现Fe与H2原子之间的键长最短,Fe与H3之间的键长最长为0.1603 nm。其中最短的H-H键长存在于H1和H2原子之间,为0.1241 nm。

表1 Cmca-FeH5的晶格常数a、b和c和Fe-Fe、Fe-H和H-H键长
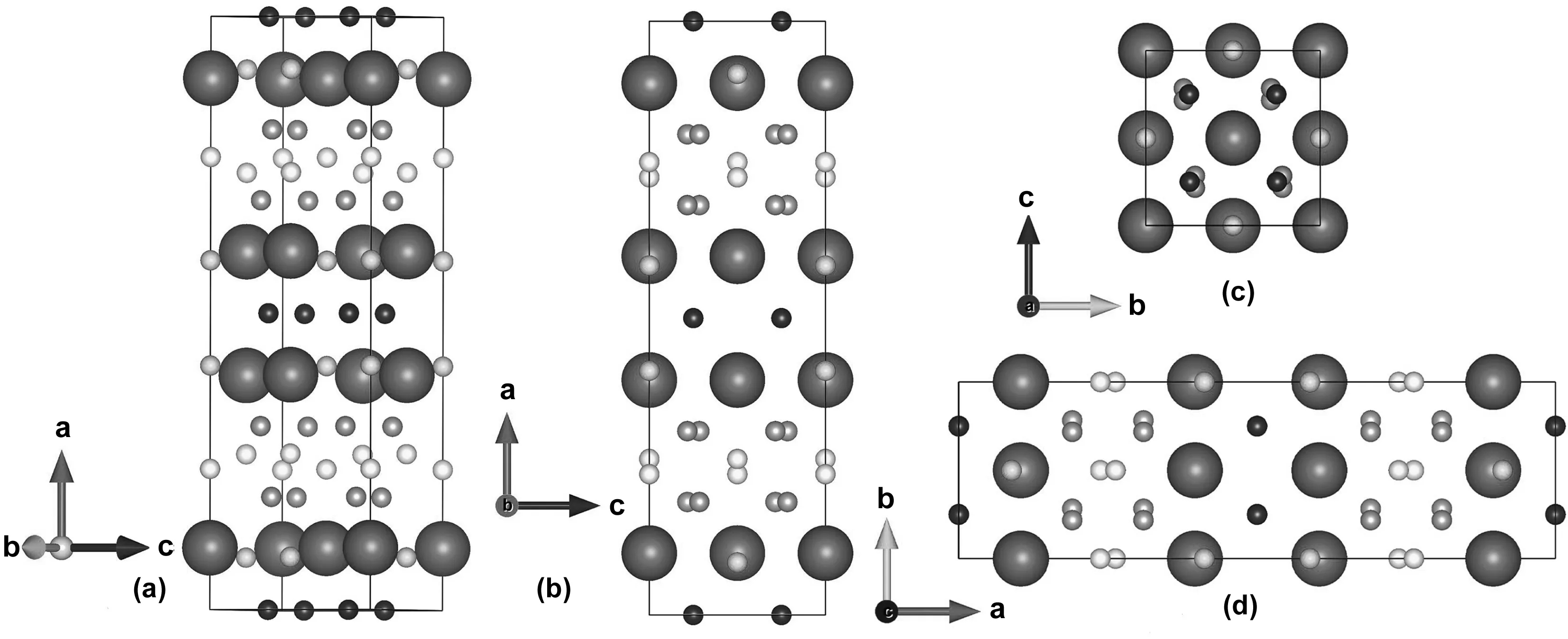
图1 (a) Cmca-FeH5晶体结构、(b)~(d)分别为 ac、bc和ab方向上的投影,其中大球代表Fe原子,小球代表H1-H4原子
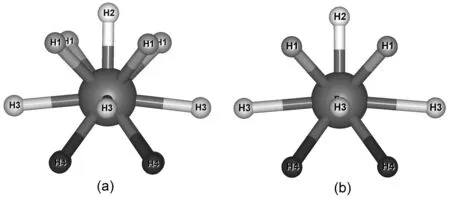
图2 (a) Cmca-FeH5和(b) I4/mmm-FeH5结构中Fe和H原子位置示意图
2.2 力学性质
2.2.1 弹性常数
材料的弹性性质可以用来描述材料受到外力作用之后抵抗形变的能力。不同晶系的材料所需表征其单晶弹性性质的独立弹性常数是不同的。表2给出了E-S和S-S两种方法计算得到的Cmca-FeH5的弹性刚度系数Cij和弹性柔性系数sij,二者互为逆矩阵。

表2 Cmca-FeH5的弹性刚度系数Cij和弹性柔性系数sij
对于正交晶系,其力学稳定性判断标准如下[25]:
Cij>0,C11+C22+C33+2(C12+C13+C23)>0,
C11+C22>2C12,C11+C33>2C13,C22+C33>2C33
(2)
计算结果表明除C44、C55和C66外,其余Cij(E-S)均比Cij(S-S)大。虽计算方法不同,得到的Cmca-FeH5的部分弹性常数存在差异,但这两种方法计算得到的Cij均满足上述力学稳定性条件。因此,Cmca-FeH5在300 GPa下是力学稳定的。
材料的形变及原子之间键合与弹性常数C11、C22和C33有着密不可分的联系。E-S和S-S方法计算的C11>C33>C22,预示着沿a轴、c轴和b轴方向上的抗压缩能力逐渐降低,沿(100)和(001)晶面内的键合能力强于沿(010)晶面的,而(010)晶面对外力的反应更加的敏感。C44、C55和C66则与材料的剪切形变相关,E-S和S-S方法计算的Cii(i=1-3)>Cjj(j=4-6)暗示了Cmca-FeH5抵抗剪切形变的能力更弱。目前的报道中尚没有关于Cmca-FeH5弹性常数的数据供我们比较,此结果能够为之后的实验研究提供数据支撑。
为了利于之后实验的对比,本文采取Vogit-Reuss-Hill[26]近似来计算Cmca-FeH5的体弹模量B[23]和剪切模量G。
B=1/2(BV+BR)
(3)
G=1/2(GV+GR)
(4)
BV=1/9(C11+C22+C33)+2/9(C!2+C23+C13)
(5)
GV=1/15[(C11+C22+C33)-(C12+C23+C13)+3(C44+C55+C66)]
(6)
BR=T[C11(C12+C33-2C33)+C22(C33-2C13)-2C33C12+C12(2C23-C12)+C13(2C12-C13)+C23(2C13-C23)]-1
(7)
GR=15{4[C11(C22+C33+C23)+C22(C33+C13)+C33C12-C12(C23+C12)-C13(C12+C13)-C23(C13+C23)]/T+3(1/C44+1/C55+1/C66)}-1
(8)
(9)
其中,BV,GV,BR和GR中下标V表示Vogit近似;R表示Reuss近似。Vogit和Reuss近似分别代表了弹性模量的上下界限。
弹性模量E和泊松比v可以由下列表达式来定义[25]:
E=9BG/(3B+G)
(10)
v=(3B-2G)/(6B+2G)
(11)
根据上述关系式,表3中给出了本文计算得到的Cmca-FeH5的B、G、E和v的数值。B>G预示着:与G相比,B是影响Cmca-FeH5力学稳定性的主要参数。E-S和S-S方法计算的v的值分别为0.37和0.32。v的数值符合金属材料的一般值(~0.3)[27],表明Cmca-FeH5具有金属特性,且大于0.26说明Cmca-FeH5具有很好的韧性。另外,还可通过Pugh标准[28],即B/G的值大于或小于1.75来判断材料具有韧性还是脆性。E-S和S-S方法计算得到的B/G值分别为3.66和2.44,均大于其分界值1.75,说明Cmca-FeH5呈现韧性。虽然两者计算得到的Cij有一些差异,但是我们发现通过Cij计算得到弹性模量等的差别很小。所以认为这两种方法计算结果都是可靠的。

表3 Cmca-FeH5的多晶体弹模量B、剪切模量G、弹性模量E、泊松比v
2.2.2 各向异性因子
材料的各向异性能反映原子沿不同方向的不同排布。准确地描述材料各向异性行为在工程科学和晶体物理中都具有重要的意义。其中材料的各向异性因子是分析其不同晶面力学性质的重要指标。
正交晶系Cmca-FeH5的各向异性参数表达式如下[29]:
A1=4C44/(C11+C33-C13)
(12)
A2=4C55/(C22+C33-2C23)
(13)
A3=4C66/(C11+C22-2C12)
(14)
其中,A1、A2和A3分别代表{100}、{010}和{001}面的各向异性参数。其值为1时,材料呈现出各向同性的性质。根据表4可知Cmca-FeH5结构的{001}-(ab)面的各向异性程度最大,其{010}-(ac)面的各向异性程度最小。Chung和Buessem[30]报道了如下各向异性分数比判据:

表4 Cmca-FeH5的各向异性因子A1、A2、A3、AB、AG、AE和AU
AB=(BV-BR)/(BV+BR)
(15)
AG=(GV-GR)/(GV+GR)
(16)
AE=(EV-ER)/(EV+ER)
(17)
这3个参数分别用于对材料B、G和E的各向异性程度判定。它们值为0,均预示材料是弹性各向同性的;值为1,预示材料有最大程度的弹性各向异性。另外,Shivakumar和Ranganathan[31]引入了适用于所有晶系的各向异性因子AU。
AU=5GV/GR+BV/BR-6
(18)
AU=0,材料表现出各向同性;其值越偏离0,表现出越大程度的各向异性。通过对A1、A2和A3,AB、AG、AE和AU这些参数的分析,Cmca-FeH5呈现了较大程度的弹性各向异性。
为了直观的反映材料的各向异性程度,本文据以下表达式[32]绘制了Cmca-FeH5随方向变化的杨氏模量E和线性压缩系数β的三维图像(图3)。
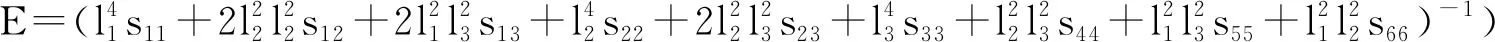
(19)
(20)
其中li(i=1-3)为方向余弦。如果所绘制的图像为球体时,该材料为各向同性。图4为两种方法计算得到的Cmca-FeH5的E和β在不同平面内的投影。可以发现这两种方法得到的E和β之间的差异比较小。由于相邻原子间的作用程度不同,E-S和S-S方法计算的Cmca-FeH5的E的最小值分别为449.1 GPa和418.5 GPa,最大值分别为1404.7 GPa和1342.9 GPa。计算的Cmca-FeH5的β最小值分别为0.31 TPa-1和0.45 TPa-1,最大值分别为0.33 TPa-1和0.54 TPa-1。
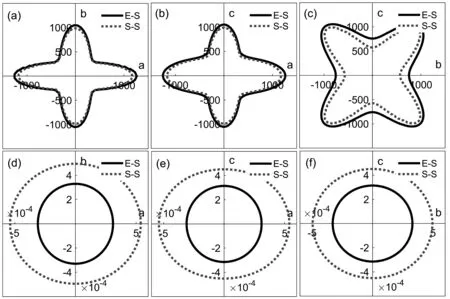
图4 (a)-(c)和(d)-(f) Cmca-FeH5的杨氏模量E和线性压缩系数β在ab、ac和bc平面的投影
2.2.3 德拜温度
德拜温度θD是计算物质热力学性质的基本参数之一,它与材料的热膨胀、熔点、Grüneise参数等物理性质有关。θD值越高,代表材料原子之间的键合能力越强。θD、平均声速vm、横向vt和纵向声速vl的定义式如下[33]:
(21)
(22)
其中h、k、NA分别表示普朗克、玻尔兹曼和阿伏加德罗常数。表5中给出了Cmca-FeH5的质量、密度、不同方向上的弹性波速及德拜温度的值。我们观察发现这两种方法计算的θD的值吻合的较好。Cmca-FeH5的θD相对较高,原子之间的键合能力较强。

表5 Cmca-FeH5的质量M、密度ρ、德拜温度θD以及不同方向上的弹性波速vl、vt、vm
2.3 电子性质
本文通过Cmca-FeH5的能带结构和电子态密度来分析其电子结构特性。图5中0eV处虚线为费米能级,从图5(a)中可以得到Cmca-FeH5的布里渊区高对称点之间能带结构中不存在带隙。从图5(b)总的电子态密度中发现在费米能级处的电子态密度N(EF)为0.12 states/eV/unit,与文献[12]计算得到的N(EF)等于7.718 states 0.14 States/eV/unit/Ry接近,证明Cmca-FeH5在300 GPa下呈弱金属性,与本文前面泊松比的判断得到的结论一致。Cmca-FeH5的电子态密度主要是Fe的3d轨道起作用,Fe原子和H原子之间存在杂化现象。
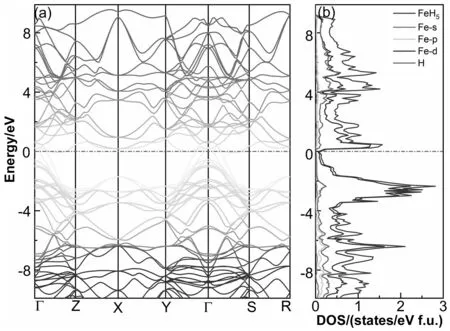
图5 (a)、(b)分别为Cmca-FeH5的能带结构、总的和分波态密度,E=0 eV为费米能级
3 结论
基于密度泛函理论采用投影缀加平面波法获得了300 GPa下Cmca-FeH5的结构信息,与先前的理论研究结果相符。能带和电子态密度分析发现Cmca-FeH5具有弱金属性。采用E-S和S-S两种方法计算了其300 GPa下的独立弹性常数,发现Cmca-FeH5是力学稳定性的。本文得到的Cmca-FeH5的多晶弹性模量表明体弹模量B是影响其力学性质的主要参数。B/G>1.75判断出Cmca-FeH5呈现韧性。通过对材料各向异性参数的计算,发现Cmca-FeH5具有较大的各向异性。另外,计算的Cmca-FeH5的德拜温度较高,其原子之间的键合能力较强。本文对以后Cmca-FeH5相关性质的研究提供了理论数据支撑。
