采用下垂控制的直流配电系统高频振荡分析及控制
2021-09-13李喜东刘发英贾善翔
彭 克,王 琳,李喜东,刘发英,张 浩,贾善翔
(山东理工大学电气与电子工程学院,山东省淄博市 255000)
0 引言
随着光伏、电动汽车等直流设备的大规模接入,传统交流配电系统正面临着电源类型多样化、负荷需求多元化、变换环节多级化等一系列复杂问题[1-2]。直流配电系统以其独特的优势得以快速发展,但也面临着诸多挑战[3-4],尤其诸多电力电子设备的接入导致系统呈现弱阻尼特性,易发生振荡。
现阶段,国内外众多学者从不同方面对直流配电系统频率振荡特性的影响因素展开了深入的研究,尤其高频振荡现象已引起诸多关注。文献[5]指出直流配电系统的电网谐波不平衡引发的高频纹波和并联在母线上多个变换器之间的交互作用导致系统不稳定而产生高频振荡。文献[6]研究发现,采用直流电压下垂控制策略的电压源型换流器(VSC)输出阻抗呈现负阻性,与线路阻抗及恒功率负荷相互作用,引发直流系统高频振荡。文献[7]指出,柔性直流配电系统互联装置存在多个时间尺度的控制环节,这些控制环节容易与交/直流线路和负荷等设备构成不同时间尺度的振荡。文献[8]针对在交/直流混合配电网中存在具有负动态阻抗的负荷引发高频振荡的问题,提出了一种分布式有源振荡抑制方法。文献[9]分析了VSC与直流系统单元的不良交互机制,发现VSC稳态功率点变化导致电压控制环节易引发高频振荡现象,提出了一种可分段调节系数的改进型有源阻尼控制器。文献[10]指出,线路等效阻抗与换流器稳压电容共同构成具有低阻尼特性的LC环节,易引发直流微电网的高频振荡,影响系统稳定性;基于阻抗匹配准则,提出一种计及低通滤波器的有源阻尼抑制方法,通过改变换流器的等效输出阻抗,使主导特征根向s域平面左移。文献[11]指出多机并网系统的阻抗耦合愈发严重,易引发高频振荡,从而使系统的稳定运行面临严峻挑战,通过在换流器输出阻抗增加串联和并联2个虚拟阻抗,提出多机并联的两带阻滤波器高频振荡抑制方法,增强系统的整体阻尼。为了分析含多VSC的高频振荡特性,文献[12]定量分析了控制系统的延时特性对于传统虚拟阻抗方法的影响,并进一步解释了虚拟阻抗在高频段易产生振荡的机理,提出一种虚拟阻抗相角补偿的高频振荡抑制方法,并通过根轨迹求得补偿函数的取值范围。
虽然目前针对高频振荡已有部分研究,但关于直流配电线路参数对系统频率振荡影响的研究较少。针对这一问题,本文对换流器控制系统、直流配电线路和恒功率负荷进行详细建模,通过频域方法分析了下垂控制参数以及直流线路参数变化对高频振荡频率的影响,提出适应于高频段的控制器设计方法,最后通过仿真验证了理论分析的正确性以及所提方法的有效性。
1 直流配电系统频域模型
1.1 直流配电系统结构
直流配电系统按照拓扑结构可分为单端、双端和多端供电方式,本文将采用基于功率-电压下垂控制策略的单端辐射状供电结构进行分析。直流配电系统的拓扑结构如附录A图A1所示。
1.2 VSC控制系统模型
换流器交流侧电流可分解为id和iq两个独立分量,有 功 功 率P与id有 关,无 功 功 率Q与iq相关[13-14],即
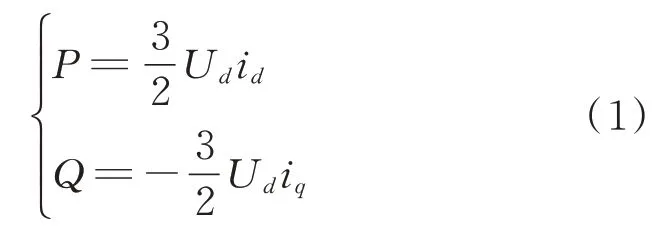
式中:Ud为换流器网侧交流电压的d轴分量;id和iq分别为网侧交流电流的d、q轴分量。
VSC的外环输出控制方式可以分为有功功率类控制和无功功率类控制两种[15-16],而频率振荡是有功功率控制过程中的小扰动问题[17],因此,本文采用典型的有功功率控制方式进行分析。解耦后的有功功率控制器框图如附录A图A2所示。图A2中,Pref为有功功率参考值,k为下垂系数,ΔUdc为直流电压的偏移量,T1和T3为时间常数,T2为外环积分时间常数,kp为外环比例增益,G0(s)为换流器采样环节,G1(s)为换流器电压外环比例-积分(PI)控制环节,G2(s)为简化的电流内环[10,18]。由图A2可得到有功功率控制器中有功功率P对直流电压偏移量ΔUdc的传递函数,体现了系统的虚拟惯量特性,传递函数为:
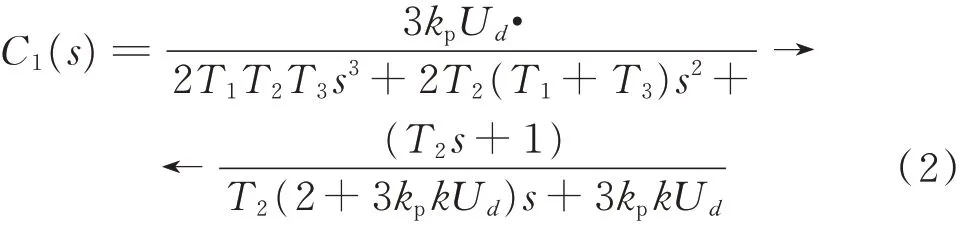
1.3 直流线路及直流负荷模型
直流线路是直流配电网区别于微电网的主要特征,因此本文将考虑直流配电线路对系统振荡频率的影响。此外,在直流配电系统中,大多数直流负荷、分布式电源和电力电子器件端口都具有恒功率特性,在对稳定工作点进行线性化后,表现为负电阻特性,如式(3)所示。

式中:R1为恒功率负荷等效成RC并联电路的电阻参数;Udc为直流母线电压;PCPL为直流负荷的额定容量。
DC/DC换流器的端口电容具有稳定电压的作用,因此可以将恒功率负荷模型等效为RC并联电路[19-20],等效模型如附录A图A3所示。其中,C1为恒功率负荷等效成RC并联电路的电容参数,Rline和Lline、Cline分别为直流线路等效电阻、电感、电容;,Ll为线路长度,r、l分别为单位长度等效电阻、电感,有

根据附录A图A3所示的等值电路,求解传递函数为:
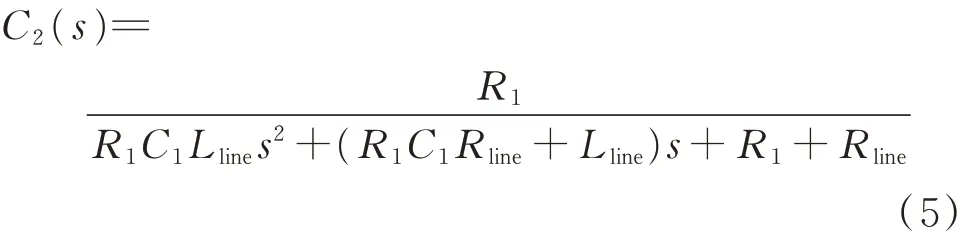
1.4 直流配电系统频域降阶建模
将下垂控制系统模型、直流负荷与直流线路的等值电路模型相串联,得到系统的整体传递函数如附录A式(A1)所示。
考虑控制系统具有较快的电气量跟随特性,可按照典型的Ⅰ型系统设计控制器,即将外环PI调节器零点抵消电流内环控制器极点[18]。可选取T2=T3后对系统的下垂控制环节进行降阶处理,得到系统整体传递函数为:
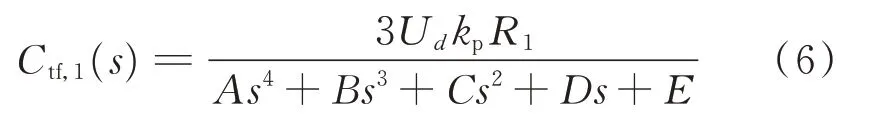
其中,
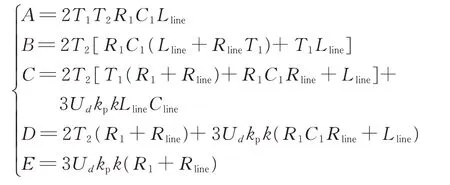
根据下垂控制环节降阶后的传递函数式(6)和原始系统传递函数式(A1)所绘制的波特图如附录A图A4所示。由图A4可知,下垂控制环节降阶前后,系统的高频振荡频率曲线基本保持一致,因此,可通过降阶系统模型对频率振荡特性进行分析。
2 频率振荡特性分析
由式(6)可知,传递函数Ctf,1(s)不存在零点或者在无穷远处存在零点。式(6)极点所对应的特征方程为:
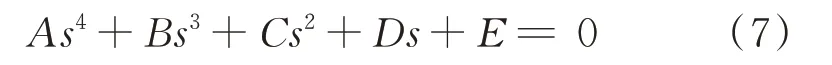
进一步化简为:
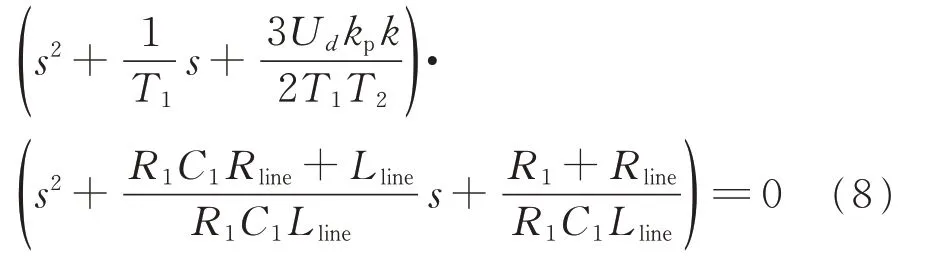
分别令式(8)等号左侧两项为0,求解特征方程的零点,即开环传递函数的极点。当式(9)被设计成欠阻尼二阶系统时(阻尼小于1且大于0),系统自然振荡频率ωn,1和阻尼ξ1如式(10)所示。
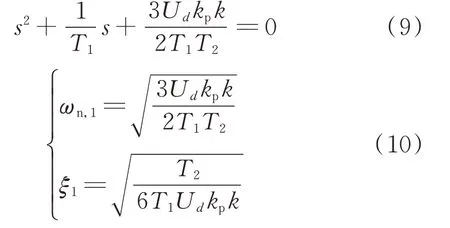
由式(10)可知,自然振荡频率及阻尼比的大小均与采样环节的时间常数T1、外环积分时间常数T2、外环比例增益kp和下垂系数k有关。
同理,当式(11)被设计成欠阻尼二阶系统时,系统自然振荡频率ωn,2和阻尼ξ2如式(12)所示。
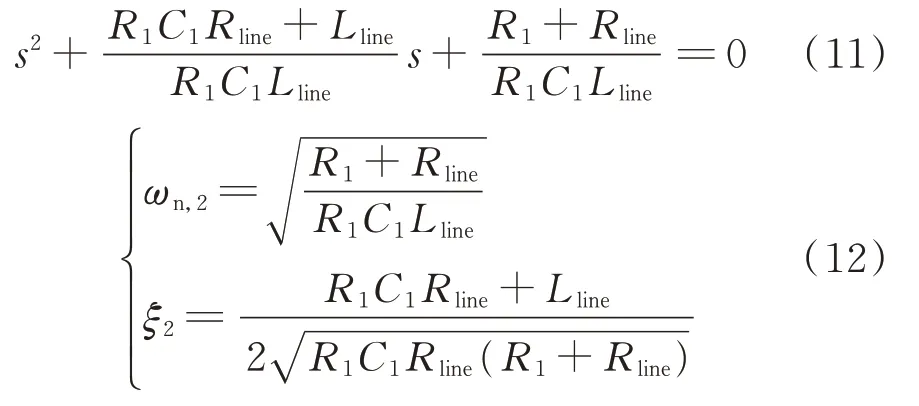
由式(12)可知,自然振荡频率ωn,2和阻尼比ξ2的大小均与线路参数Lline和Rline的大小以及恒功率负荷等效成RC并联电路的等效参数R1和C1的大小有关。
2.1 控制系统参数变化
根据自然振荡频率ωn,1可知,下垂控制环节振荡频率的影响因素为电压外环PI系数以及下垂系数k,且与kp及k的大小成正比。电压外环比例增益kp及下垂系数k变化时所对应的振荡频率波特图分别如图1和附录A图A5所示,振荡频率与计算频率对比情况如附录B表B1和表B2所示。
如图1和附录A图A5及附录B表B1和表B2所示,随着kp及k的增加,振荡频率增大,与理论分析结果一致,验证了理论分析的正确性。
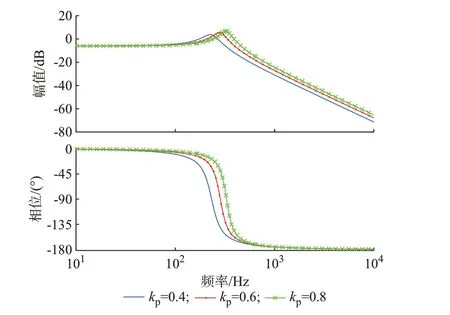
图1 变电压外环增益频率振荡曲线Fig.1 Frequency oscillation curve with variable voltage outer loop gains
2.2 直流线路参数变化
1)电阻参数对高频振荡的影响
根据换流器直流侧系统自然振荡频率ωn,2可知,振荡频率的大小与直流线路参数Rline变化成正相关,与参数Lline变化成反比。在分析直流线路电阻值变化对系统稳定性的影响时,直流线路电感值保持不变。假设单位线路长度电阻值为0.05Ω/km,分别选取线路长度为3、6、9 km,相应电阻值Rline分别为0.15、0.3、0.45Ω,改变线路电阻参数所对应的频率振荡曲线如附录A图A6所示,振荡频率与计算频率对比情况如附录B表B3所示。由图A6及表B3可知,增大线路Rline参数会提升系统阻尼、减小振荡频率的幅值且对振荡频率变化影响较小。
2)电感参数对高频振荡的影响
同理,在分析直流线路电感值变化对系统稳定性的影响时,直流线路电阻值保持不变。假设单位线路长度电感值为0.1 mH/km,分别选取线路长度为3、6、9 km,相应电阻值Lline分别为0.3、0.6、0.9 mH,改变线路电感参数所对应的频率振荡曲线如附录A图A7所示,振荡频率与计算频率对比情况如附录B表B4所示。由图A7及表B4可知,增大线路参数Lline,振荡频率降低。
2.3 直流负荷变化
对直流配电系统中直流负荷的接入数量进行分析如附录A图A8所示,振荡频率与计算频率对比如附录B表B5所示。由图A8和表B5可知,直流负荷接入数量会对系统振荡频率产生影响,随着恒功率直流负荷的增加,振荡频率向更低的频段移动。
3 高频控制器设计
3.1 串联系统频率振荡特性分析
当n个线性系统的传递函数串联时,其等效系统传递函数等于串联系统中n个传递函数的乘积,即:
图3为活性炭基脱氯剂AC-101和CT-01I粉末的XRD图。分析可知,在AC-101和CT-01I中均检测到了活性炭及CuO物相的存在,但并没有检测到Na2O的存在。即便如此,活性炭载体上存在的NaOH也可用来脱氯。此外,SEM的元素分析表明,该脱氯剂中w(Cu)=5.10%,w(Na)=3.96%,与对照组脱氯剂活性组分的含量相近。
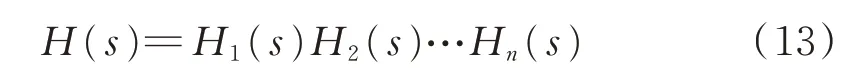
或者
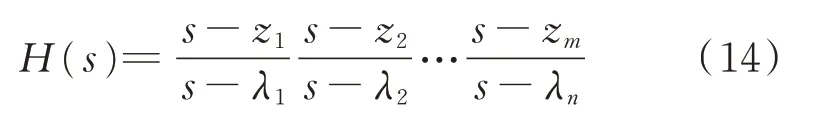
式中:z1,z2,…,zm为串联系统的零点;λ1,λ2,…,λn为串联系统的极点。由传递函数的串联特性以及式(14)可知,n个独立线性系统传递函数零、极点共同构成串联系统传递函数的零、极点,串联的各个独立系统间的零、极点分布不会相互影响。由于系统的频率动态特性受传递函数零点和极点分布的影响,故系统整体的频率动态特性等于各个独立传递函数频率特性的叠加。
因此,鉴于下垂控制环节、直流侧线路与负荷等均可导致高频振荡现象,本文针对这2个环节提出适应于不同频率振荡特性的控制器设计方法。
3.2 考虑下垂环节影响的高频控制器
为了提高下垂控制系统的阻尼特性,在下垂环节的前置环节引入前馈控制器,通过反馈直流电流的形式将在控制器的设计中考虑直流线路参数,对下垂控制环节的阻尼提供正向支撑,抑制下垂控制器k、kp参数变化所导致的高频振荡问题,提高系统稳定性。本文提出的高频控制器设计方法以及VSC的控制框图如图2所示。
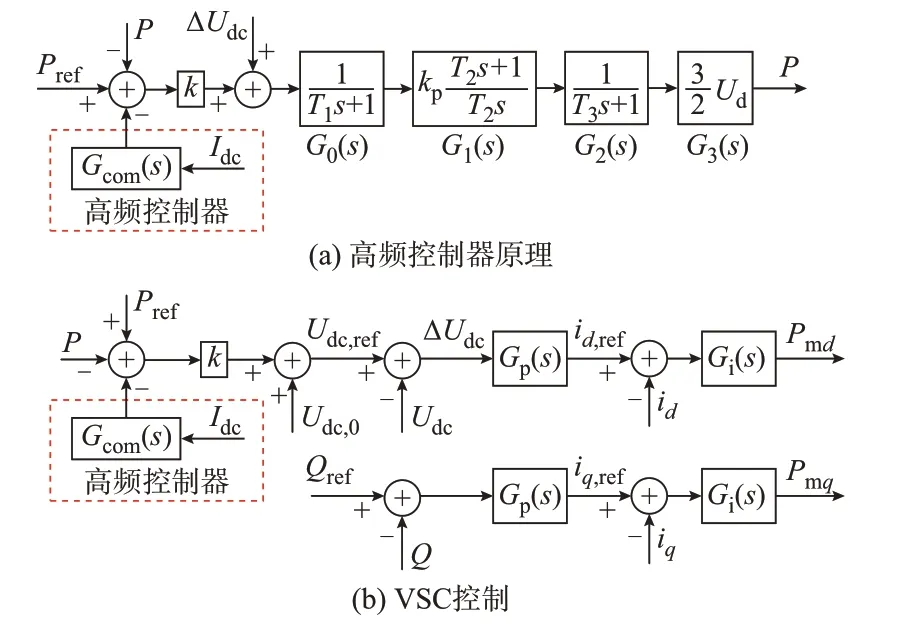
图2 高频控制器原理及VSC控制框图Fig.2 Block diagram of high-frequency controller principle and VSC control
图2中:Pref和Qref分别为有功和无功功率参考值;Idc为直流电流;Gp(s)和Gi(s)分别为换流器电压外环和电流内环比例-积分控制环节;Udc,ref和Udc,0分别为直流电压的参考值及稳态值;Pmd和Pmq分别为换流器调制解调信号的d、q轴分量;id,ref和iq,ref分别为电压外环控制器产生的d、q轴电流信号参考值。
阻尼补偿函数Gcom(s)表达式为:
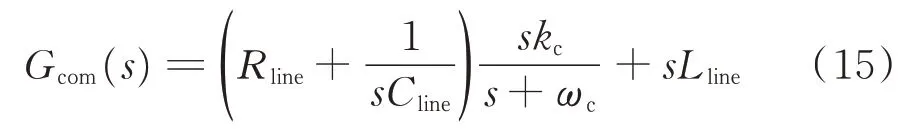
式中:kc为高通滤波器增益;ωc为截止角频率,由式(15)可知,下垂控制环节高频振荡控制器由阻性、感性和容性参数共同组成,当系统存在外部扰动时,换流器出力变化引起直流电流Idc相应发生改变。此时,控制器中阻性参数提供的阻尼与换流器的出力成正相关,可以有效抑制系统高频振荡。为解决控制器中直流电流稳态分量馈入的问题,采用一阶高通滤波器滤除直流电流的稳态分量;控制器中各感性分量存在微分环节,即换流器出力发生变化时,可以快速响应,为系统提供阻尼抑制高频振荡。
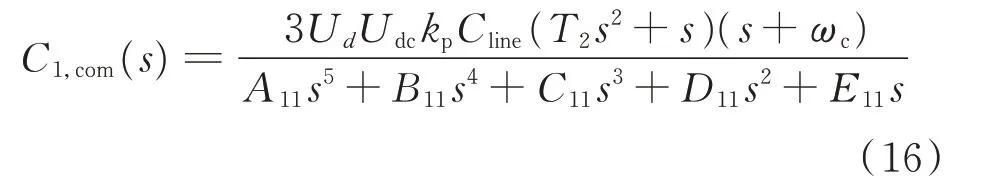
其中:
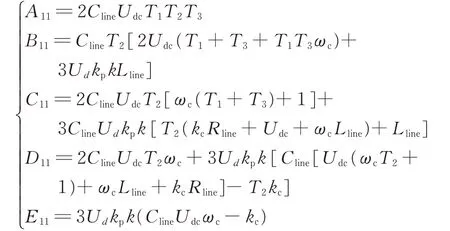
3.3 考虑直流线路侧影响的高频控制器
直流线路是直流配电系统的重要组成部分,但线路电阻、电感参数增大会导致阻尼减弱;且恒功率负荷呈负电阻特性,随着负荷的增加阻尼下降。因此,考虑直流侧线路的影响进行高频控制器的设计尤为重要。目前换流器弱阻尼状况下的虚拟阻抗补偿方法主要通过阻容性虚拟阻抗[7,21]或者阻感性虚拟阻抗[22]的方式进行补偿,使系统保持较大的正阻性,而对于直流线路参数引发高频振荡的研究较少。因此,为了缓解直流线路及负荷阻尼减弱引起的直流电压增幅振荡,采用改进虚拟阻抗的形式,在直流侧等效模型中反向串联一个受直流电流Idc控制的阻尼补偿电压Δudc,如附录A图A9所示。如果补偿电压与扰动电压大小相等、相位相反,则可以有效抑制母线电压的增幅振荡。Δudc的表达式为:

式中:Rv为虚拟阻抗。
改进虚拟阻抗的控制方式不仅可以增强系统阻尼,还可以避免仅采用虚拟阻抗时的母线电压调节困难问题[23]。校正后的直流线路及直流负荷等效模型和控制原理框图如附录A图A9和图A10所示,传递函数如式(18)所示。
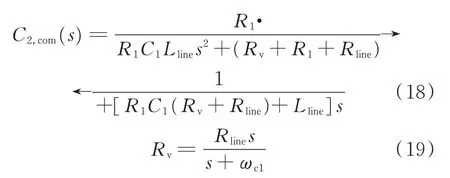
式中:ωc1为一阶高通滤波器的截止角频率。考虑虚拟阻抗后,式(18)所对应的阻尼比如式(20)所示。由式(20)可知,引入虚拟阻抗后,阻尼比ζ2,com的分子项呈指数关系增长,阻尼增强效果明显。
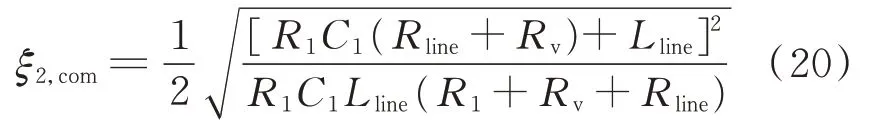
本文提出的上述2种控制器共同施加于控制系统时,可以有效抑制由下垂控制器外环比例增益、下垂系数、直流线路参数以及恒功率负荷引起的高频段振荡。
4 仿真分析与验证
下文将借助MATLAB/Simulink软件进行建模仿真,按附录A图A11所示结构搭建了低压直流配电系统详细模型,以单端辐射状配电结构作为研究对象,对直流配电系统进行仿真。控制方式包括施加考虑下垂控制环节影响的高频控制器(简记为CK)、施加考虑线路侧影响的高频控制器(简记为CL)以及两者共同作用(简记为CKL),分析不同控制器设计方法对系统高频振荡特性的影响。系统参数如附录B表B6所示。
4.1 CK控制方式分析
施加CK控制方式前后的直流母线电压波形和频率振荡曲线如图3和附录A图A12所示。
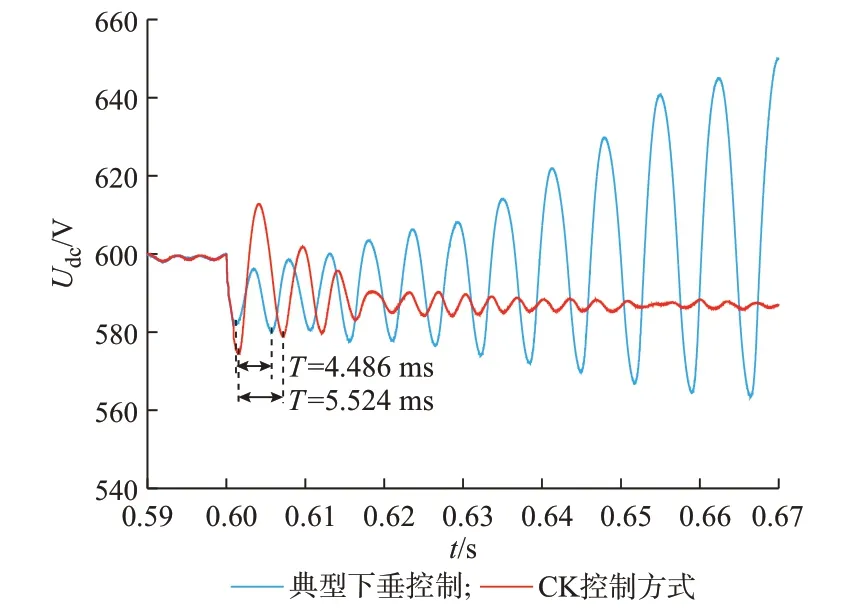
图3 施加CK控制前后电压波形Fig.3 Voltage waveforms before and after applying CK control
从附录A图A12可知,施加CK控制方式后,频率振荡曲线的峰值降低。如图3所示,当换流器运行于典型下垂控制方式下,在0.6 s时直流配电系统负荷扰动,负荷容量变为原来的1.2倍,直流母线电压发生高频振荡,振荡周期T=4.486 ms(约223 Hz),且为增幅振荡。采用CK控制方式后,振荡幅值得到明显抑制,母线电压趋于稳定。因此,所提CK控制器设计方法可以有效增强控制系统阻尼特性,达到抑制下垂控制环节高频振荡的效果。
4.2 CL控制方式分析
施加CL控制方式前后换流器直流侧系统的直流母线电压波形和频率振荡曲线如图4和附录A图A13所示。

图4 施加CL控制前后电压波形图Fig.4 Voltage waveforms before and after applying CL control
从附录A图A13可知,考虑CL控制器后,换流器直流侧系统的频率振荡曲线的峰值降低。如图4所示,典型下垂控制下的直流系统在0.6 s时发生负荷扰动,负荷容量变为原来的1.2倍,引起直流母线电压高频增幅振荡,振荡周期为3.488 ms(约287 Hz)。采用CL控制方式后,母线电压增幅振荡问题得到明显改善,母线电压趋于稳定。因此,CL控制器的设计方法可以有效增强控制系统阻尼特性,高频振荡抑制效果较好。
4.3 CKL控制方式分析
4.1和4.2节分别针对CK和CL控制器设计方法进行仿真分析,本节将对两者共同作用下的直流配电系统频率振荡特性进行仿真。频率振荡曲线如附录A图A14所示,CKL控制方式下的直流母线电压波形如图5所示。
由图A14可知,直流配电系统运行于CKL控制方式时,可以增强整个直流配电系统的阻尼特性,有效抑制下垂控制系统、直流线路和负荷引起的高频振荡。如图5所示,直流系统运行于典型下垂控制方式下,在0.6 s时发生负荷扰动,负荷容量变为1.2倍,直流母线电压发生高频振荡,振荡周期为4.486 ms(约223 Hz),为增幅振荡。而运行于CKL控制方式下,直流电压振荡现象得到明显抑制,母线电压趋于稳定。
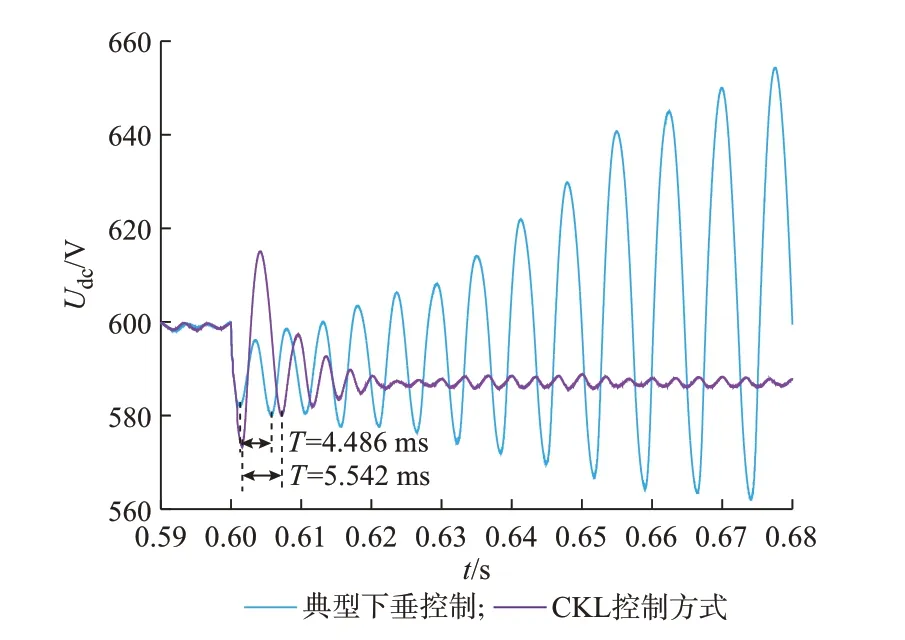
图5 典型下垂控制和CKL控制电压波形图Fig.5 Voltage waveforms with typical droop control and CKL control
由图6可知,运行于CKL控制方式下的直流配电系统较CK控制方式时阻尼特性增强明显,抑制电压振荡效果更好;相较于CL控制方式,运行于CKL控制方式下的直流配电系统母线电压趋于稳定的时间更短,阻尼及动态特性更好。
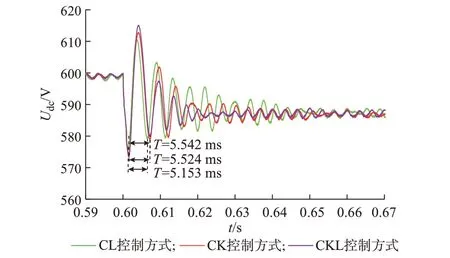
图6 CL、CK和CKL控制方式下电压波形图Fig.6 Voltage waveforms with CL,CK and CKL control
综上可知,本文提出的CK和CL高频控制器均可以实现增强系统阻尼、抑制直流母线电压振荡的目的,而且两者共同作用时抑制效果最好,仿真结果验证了所提设计方法的有效性。
5 结语
本文对典型直流配电系统进行频域建模,从高频振荡的角度对直流配电系统进行研究。针对系统存在的弱阻尼以及负阻尼特性,提出了适应于高频段的控制器设计方法,有以下结论。
1)直流配电系统的控制环节和物理电路环节均会引起直流电压的高频振荡现象。
2)CK高频控制器可以有效改善典型下垂控制环节引起的弱阻尼等问题。CL高频控制器可以有效增强直流线路侧系统阻尼特性,且高频振荡抑制效果较好。
3)系统运行于CKL控制方式下时,可以抑制控制环节与物理电路环节引起的高频振荡,控制效果优于CL与CK控制器。
光伏、储能等直流型电源接入直流配电系统对系统频率振荡特性的影响以及控制优化方法有待在后续工作中进一步深入研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
