计及用户体验度的家庭用电设备建模及优化分析
2021-09-13李满东吴志学刘潇武广泉罗安段嘉昭
李满东,吴志学,刘潇,武广泉,罗安,段嘉昭
(国网北京顺义供电公司,北京 顺义101300)
随着人们生活水平的日益提高,家庭用电在电力消费中所占的比重越来越大,因此引导家庭用电往智能化方向发展可以在削峰填谷、节能减排、提高经济社会可持续发展等发面发挥越来越重要的作用。根据家庭用电负荷的特性,许多学者对家庭用电设备优化进行了深入的研究。文献[4]对不同类型的家庭用电设备进行建模和分析,实验结果表明合理的调节家庭用电设备的工作时间,不仅可以节省家庭电费支出,还可以对电力市场中日前市场的波动起着平衡作用,同时在消纳太阳能等可再生能源中产生很大的经济效益。文献[5]依据实时电价研究家庭用电的智能优化方法,在计及用户舒适度的情况下,以减少家庭电费支出为优化目标提出优化策略,并且考虑了优化后可能出现峰谷倒置的情况,提出改进家庭用电优化的方法。文献[6]以经济性和舒适度为目标建立优化模型,使用遗传算法仿真分析,添加比例系数进行优化调节。文献[7]建立的目标函数是效用因数和电费之差,并且考虑了权重因数,根据用户的喜好不同设置不同的权重因数进行体验度和成本之间的权衡。文献[8]提出了模糊关联权重法,根据用电设备的相关因素值对模型优化求解,结果显示,合理的优化家庭用电设备能削峰填谷,同时节省用户的电费支出,模糊权重法能快速正确的帮助用户选择停止运行的设备。文献[9]是在以电费为目标对家庭用电设备建模时重点考虑了用电设备之间的关联度,并设计出家庭用电设备之间的关联度实时更新的方案。文献[10]使用Gurobi软件包降低了求解问题的难度。文献[11]通过实际算例验证改进遗传算法的有效性,但都是对单个目标优化,而没有考虑多目标优化。文献[12]将随机模拟结合粒子群算法对模型优化,根据设置的置信水平的不同来反映约束条件被随机变量的影响程度。
基于此,本文根据家庭用电设备的负荷特性分别建立不可中断设备和可中断设备的模型,提出了计及用户体验度的家庭用电优化模型,采用遗传算法对用电费用和用户体验度分别进行优化求解,采用NSGA-II算法进行两个维度的优化。
1 家庭用电系统的模型
1.1 家庭用电设备的分类
本文以某家庭的用电系统为研究对象,根据用户对用电设备的使用情况分为基础设备、不可中断设备和可中断设备等3类设备。
基础设备:主要有照明、电视机、电脑、冰箱等,这类设备与用户的个人喜好和作息时间联系紧密,一旦发生改变,会给用户带来极大的不便,不参与家庭用电的优化调度。
不可中断设备:主要有洗衣机、洗碗机、电饭煲等,用户对这类设备的使用不是即时的,只要在合适的时间段内完成任务即可,但在使用过程中不能停止,否则会影响用户的生活体验。
可中断设备:主要有吸尘器、空调等,这类设备在停止运行一段时间后再运行不会特别影响用户的使用体验,可以适当的结合分时电价来选择设备的工作时间。
家庭中重要的基础设备不参与用电的优化调度,由于不可中断设备和可中断设备的可转移运行时间的特性,因此家庭用电设备能量优化主要是对不可中断设备和可中断设备进行的优化。
1.2 家庭用电设备的建模
为了方便描述用电设备的运行状态,引入开关量;当开关量的值为1时表示设备a在k时段处于运行状态;当开关量的值为0时表示设备a在k时段处于停止运行状态。那么设备a在一天的24小时内的运行状态可表示为:
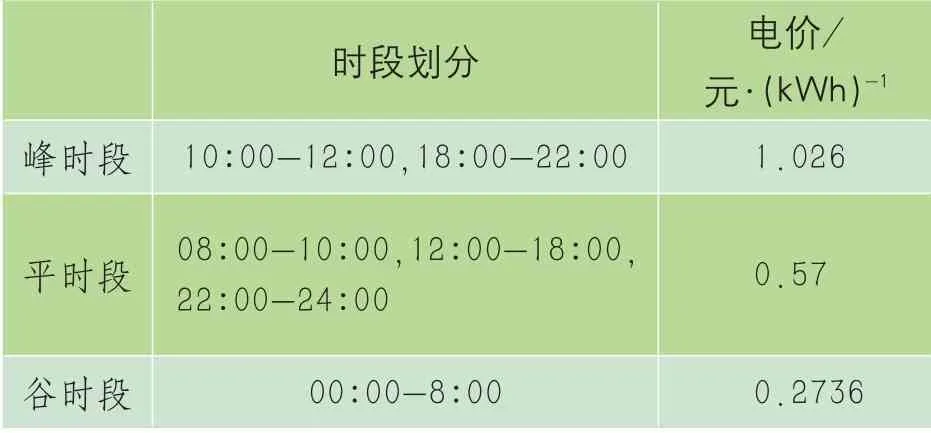
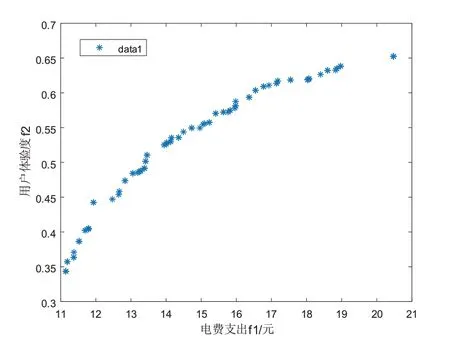
若设pa为设备a在正常可运行时间内的最早开始运行时间段;qa为设备a在正常可运行时间内的最晚结束运行时间段;则有pa 本文假设设备在运行时的功率恒为额定功率Q,停止运行时的功率为0,若在一个小时均分为n个时间段的情况下,则设备在k∉[pa,qa]时的功率为0,设备在k∈[pa,qa]时的每个时间段的功率为q,那么Q和q的关系为:q=Q/n。 1.2.1 不可中断设备的模型 由于不可中断设备一旦开始运行,就需要连续运行直至达到完成任务所需要的时间段数,在运行期间不能中断运行,比如电饭煲一旦进入运行状态,无论现在的电价如何,都保持运行状态直到工作结束,此类用电状态示意图如图2所示,则不可中断设备满足的约束条件可表示如下。 不等约束条件为: 式中:tstart为设备实际开始运行的时间;tend为设备实际结束运行的时间;pa为设备a最早可以开始运行时间;qa为设备a最晚需要结束运行的时间;Da为设备a完成运行任务所需要的时间段。 等式约束条件为: 式中:为设备a在时间段k时的运行状态,设备在正常运行时为1,运行停止时为0;Da为设备完成运行任务所需时间段;Ea为设备a在完成Da时间段的任务时消耗的总电能。 1.2.2 可中断设备的模型 由于可中断设备只需要保证在可运行的时间段内完成运行所需要的时间段即可,可以在可运行时间段中临时中断设备运行,此类设备运行示意图如图3所示,若设备在可运行时间段内完成运行任务,可以根据分时电价信息,在电价较高时选择中断运行,电价较低时选择运行,总的运行时间段之和保持不变即可。 图3 可中断设备运行示意图 不等约束条件与公式(1)~(3)相同。 等式约束条件为: 1.3.1 用电费用的模型 首先,大部分的家庭用户会在不影响正常用电需求的情况下尽可能的减少用电费用支出,所以以用电费用最少为目标建立数学模型,可以通过改变设备的运行时间,以达到经济性最优的目的,则其目标函数为: 式中:为是设备a在时刻k时的运行状态;pk为是在k时刻的分时电价信息;为设备a在时刻k时的功率大小,M是家庭中的可以参与调度改变用电时刻的用电设备的数目,N为一天划分的时间段数。 1.3.2 用户体验度的模型 本文提出家庭用户对用电设备的体验度模型,即每个家庭用电设备都有最合适的运行时刻,若设备在合适的运行时刻工作时的体验度最大,最大值为1,而离最合适的运行时刻越远,体验度越小,衰减幅度类似于反比例函数,即在时刻k时的体验度可表示为: 式中:|Δk|为设备最合适运行时刻与k时刻的时间间隔;is为常量,其大小和设备运行的时间长短有关,设备运行时间越长,is越大。本文的is取值在1~5之间。 在家庭中所有用电设备的体验度可以用平均体验度水平来表示,即: 式中:表示用电设备a在时段为k时的体验度;表示用电设备a在时段为k时的运行状态。 当家庭用户对用电设备的体验度最大为目标进行优化时,其目标函数为: 遗传算法是模拟自然环境中生物的遗传和进化机制而形成的全局优化搜索算法,它是一种并行的、高效的全局搜索方法,能自适应地控制搜索过程以达到全局最优,非常适合对复杂的非线性模型寻找最优解,本文采用遗传算法对家庭用电优化模型求解。而NSGA-II算法的快速非支配排序使得算法的复杂度大大降低,引入的精英策略增加了采样空间,同时保证进化过程中的优良个体不被抛弃,提高了优化结果的准确率,而引入的拥挤度和拥挤度算子不再需要制定共享参数,是将拥挤度作为群体中个体的准则进行比较,保证了种群的多样性。在处理多目标、非线性、复杂问题时能得到Pareto最优解集。NSGA-II算法是目前处理多目标优化问题的算法中最高效、影响范围最大的优化算法之一,具有运行速度快、收敛性强等优点,因此本文可采用NSGA-II算法对用电费用和用户体验度两个目标进行多目标优化求解。 为了方便描述,将家庭用电的优化周期T设置为一天24 h,将1 h等分成n个相同的时间段,那么一个时间段的时长为ΔT=1/n,一天24 h则可以分为N=24n个相同的时间段,对一天的24 h的N个时间段排序编号为1~N,从理论上讲,N越大,时间段越多,在计算时误差就越小。本文以30 min为一个调度时间段,即n的取值为2,那么一天的24 h就被分成48个时间段,各个用电设备的运行时长为30 min或30 min的整数倍,如果运行时长不足30 min可以按照30 min近似计算,此时的误差比以1 h为一个时间段小。电价采用的是湖北省武汉市的分时电价,分时电价信息如表1所示。 表1 分时电价信息 本文对某个家庭可进行优化调度的4个不可中断设备洗衣机、洗碗机、电饭煲A、电饭煲B和6个可中断设备空调A、空调B、吸尘器、热水器、饮水机A、饮水机B进行仿真验证,统计得到该家庭对这些设备的正常可运行时间段、使用时长、负荷功率等相关信息如表2所示,最舒适时刻相关信息如表3所示。 表2 可调度家庭用电设备相关信息 表3 可调度家庭用电设备最舒适时刻相关信息 3.2.1 单目标优化 遗传算法的相关参数设置如表4所示,种群的规模设置为100,最大迭代次数I为300次,交叉概率Pc为0.99,变异概率Pm为0.10。 表4 遗传算法参数设置 优化后,以用电费用最少为优化目标优化后随迭代次数增加电费支出情况如图2所示。 图2以用电费用为目标时优化前后各时间的用电量对比。 以用户体验度为目标进行优化后随迭代次数增加电费支出情况如图3所示。 图3 用户体验度随迭代次数的变化示意图 图3以用电体验度为目标时优化前后各时间的用电量对比 3.2.2 多目标优化 使用NSGA-II算法进行用电费用和用户体验度为目标的多目标优化所设置的参数如表5所示。 表5 NSGA-II的参数设置 图4为初始种群分布,图5为优化结果得到的Pareto最优解集,经过两个图比较可知,使用该算法优化后能得到一组有效分散分布的Pareto最优解集。对于图7偏左侧的解的用电费用较低而用户体验度较低,适合于追求电费较低的用户选择;偏右侧的解的用电费用较高而用户的体验度较高,适合于追求体验度的用户选择;中部的解兼顾用电费用和体验度,适合兼顾两个目标的用户选择。 图5 优化得到的Pareto最优解集 多目标优化后分别得到单个目标最优时的两组解,随迭代次数变化及决策变量分布图如图6、图7、图8、图9所示。 图6 用电费用单个目录最优时随迭代次数变化示意图 图7 用户体验度单个目标最优时随迭代次数变化示意图 图8 用电费用单个最优时决策变量分布图 图9 用户体验度单个最优时决策变量分布图 优化电费支出时,该家庭一天的可调度设备的电费支出降低2.76元,节省19.78%的用电费用。 优化用户体验度时,该家庭一天的可调度设备使用体验度最大达到0.6383,相对于优化前提高了24.4%。其次利用NSGA-II算法对电费支出和用户体验度两个目标为模型进行多目标优化仿真,仿真结果得到Pareto解集和单个目标最优时的解,用户可以根据结合电费支出和体验度并结合自身情况对Pareto的解集中的方案作出决策。因此对算例的仿真分析也验证了优化算法和模型的有效性和可行性。 本文建立了计及用户体验度的家庭用电设备优化模型,在考虑用户的电费支出的同时,兼顾用户对用电设备的体验度。采用常规的遗传算法对单目标模型求解,采用带精英策略的非支配排序的遗传算法(NSGA-II)对多目标模型求解,仿真结果表明,合理的安排家庭用电设备的工作时间不仅可以降低用户的电费支出,还能提高用户用电的体验度,验证了所提模型的正确性。随着新能源技术的快速发展,光伏发电、电动汽车等分布式发电和储能设备应用在一部分居民用户中,因此接下来可以将此类设备纳入家庭用电优化的研究范围中。


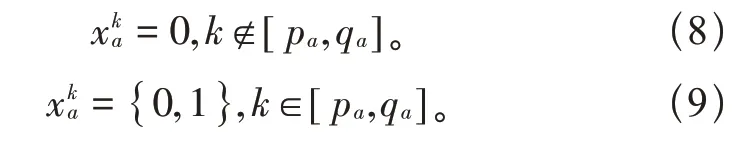

1.3 家庭用电系统的优化模型


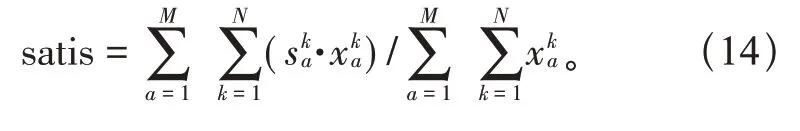

2 家庭用电设备的优化算法
3 算例仿真与分析
3.1 算例介绍


3.2 仿真分析







4 结束语
