无中心多点到多点配送问题建模与求解

卢炜达 罗世平

[摘要]针对外卖配送客户与订单随机产生，外卖骑手劳动强度极大但服务效率不够高等问题，提出无配送中心的多点到多点配送问题建模思路，并基于启发式算法求解。算例选用常见的10个订单业务，在一个社区内随机选择10个取货点和10个送货点，求解证明骑手一个小时内可以完成任务，方案可行有效。

[关键词]外卖配送;无中心;多点到多点;遗传算法

[中图分类号]F224.0;F252.14[文献标识码]A[文章编号]1005-152X（2021）12-0090-06

Modeling and Solution of Multiple-start/end Acentric Distribution Problem

LU Weida1，LUO Shiping2

（1. School of Business，Macau University of Science & Technology，Macau 999078;

2. School of Mathematical Sciences，South China Normal University，Guangzhou 510631，China）

Abstract：Due to the randomness of takeout delivery orders as well as their destinations，deliverers often have to work intensively at low service efficiency. In light of this，we proposed the line of thinking for the multi-point to multi-point distribution model without a distribution center，and solved it using the heuristic algorithm. Next through a numerical example involving ten common orders，we randomly selected 10 pickup points and 10 delivery points in a community，and applied the model to prove that a deliverer could complete its task within an hour，concluding that the model was feasible and effective.

Keywords：takeout delivery;acentric;multi-point to multi-point;genetic algorithm

0引言

外卖已经成为人们生活不可或缺的部分。截至2021年6月，我国网上外卖用户规模达4.69亿。外卖行业市场规模达到了6 646.2亿元[1]。外卖骑手在配送工作中，为了提高效率以滿足客户和公司的要求，经常超负荷工作或违反相关法律法规，造成人员伤亡。如2017年上半年，上海市公安局交警总队数据显示，在上海平均每2.5天就有1名外卖骑手伤亡。同年，深圳3个月内外卖骑手伤亡12人。2018年成都交警7个月间查处骑手违法近万次，事故196件，伤亡155人次，平均每天就有1个骑手因违法伤亡。2018年9月广州交警查处外卖骑手交通违法近2 000宗[2]。外卖骑手承受着巨大的压力，外卖工作存在大量安全隐患。因此急需合理有效的外卖配送解决方案来满足社会需求。

1问题描述

外卖配送作业通常是骑手在收到客户通过平台下单的信息后，赶到下单店铺取货并送达客户指定的目的地。为骑手提高工作效率，往往会多单并行操作，赶到多个订单所表述的多个取货点取货并送达多个目的地，即遍历订单中全部的取货点和送货点，如图1所不。但该问题具有以下特点：（1）不同于典型TSP问题[3]不分先后的简单遍历，而是需要先取货再送货;（2）取货顺序不一定按订单顺序，送货顺序也不一定完全与取货顺序相同;（3）送货不一定完成全部订单的取货后再开始，可以是边取边送。

外卖配送问题不同于一般的物流配送和VRP问题[4-5]，如图2所示。典型的物流配送和VRP问题，是从配送中心取货后，按单送到多个目的地，实现一到多的配送。外卖配送具有如下特性：（1）客户及订单的随机性。客户及订单的随机性使得配送线路及取货、送货顺序具有动态性。需要根据每组订单实时动态规划配送线路。（2）对时间的强烈要求。不同于一般电商平台购物，外卖客户下单后对等待时间有非常高的期待，一般不能超过一个小时，且追求越快越好！同时，卖家的商品需要准备时间，很难做到下单即取。（3）无配送中心和中转接驳站。骑手取货后不必返回公司，也不能由配送中心安排订单顺序，而是根据平台信息，边取货边送货。

因此，外卖配送问题可描述为无配送中心的多点到多点的配送问题。

2研究现状

外卖问题与VRP和TSP问题非常相似，又不完全一样。VRP自Dantzig和RamseF于1959年提出后即受到学术界极大的关注。围绕VRP的理论模型、应用环境及求解方法，呈现出大量的研究成果。

2.1VRP问题及其数学建模研究

VRP问题经由Dantzig等学者研究总结分成不同的类型。主要有：（1）经典旅行商问题[3]（Traveling Salesman Problem，简称TSP）;（2）带时间窗[6，7]的车辆路线问题（Vehicle Routing Problem with Time Windows，简称VRPTW）;（3）带容量限制的车辆路径问题（Capacitated Vehicle Routing Problem[8]，简称CVRP）;（4）优先约束车辆路线（Vehicle Routing Problem with Precedence Constraints[9]，简称VRPPC））;（5）随机需求车辆路线问题（Vehicle Routing Problem with Random Demand[10]，简称VRPRD）等问题。

所有模型的目标函数都是以总成本最优为目标的变形，如总里程最小、总时间最短等。

2.2VRP求解方法研究

VRP的求解主要包括传统数学优化方法和现代计算机算法。其中传统数学优化方法主要有：（1）先安排路线后分组的方法[11]（Route First-Cluster Second）;（2）先分组后安排线路的方法（Cluster First- Route Second）;（3）节约-插入算法[l2]（Saving-Inserting Algorithm）;（4）改进-交换法（Improving-Exchange Algorithm）;（5）基于数学规划的算法[13]（Mathematical Programming Based Algorithm）;（6）交互式优化算法[14]（Interactive Method）。现代计算机算法主要有：（1）人工神经网络[15];（2）蚁群算法[16];（3）遗传算法等。此外，分枝定界法和动态规划法也是较常用的求解VRP问题的算法。

2.3外卖配送优化研究

国内关于外卖行业众包物流的研究较多，包括以最后一公里的视野研究外卖配送问题。王文杰，等[17]在随机配送需求的情形下，同时考虑了众包配送的配送人员特性以及订单损失成本，研宄了众包物流配送的定价问题。方婷[18]分析了众包物流配送的风险。李玉，等[19]采用演化博弈的研宄方法，从发货商的角度出发，研宄了在保价制度下配送方的行为决策。

综上所述，尚没有见到把外卖问题定义为无中心多点到多点配送问题的研究。

3建模与分析

本文考虑情况，给定订单（O₁，O₂，…，O_n）的取货地点（R₁，R₂，…，R_n）和目标地点（T₁，T₂，…，T_n），取货地点与目标地点一一对应，即订单O_i从地点R_i取货并按要求送到T_i。不考虑多个订单在同一地点取货，或多个订单送到同一地点，甚至混合交叉的情形。基于外卖骑手的特定行为能力，本文不考虑物流路径优化中的路线方向（包括机动车限行规定等）及载货能力与装载顺序的限制等。

以骑手当前所在位置为任务的起始点，完成全部订单送货即结束，不考虑之后的行程。设从任一送货点开始，每个任务必须经过全部的R_i（i=1，2，…，n），和T_i（i= 1，2，…，n）。在上述条件下，本文的目标是找到总路程最短的路径。

外卖配送任务是一个有条件限制的TSP问题。每个订单的履行，必须是先取货，后送货，即R_i在T_i之前（i= 1，2，…，n）。

设任意两点i，j距离为C_ij，则目标函数为：

设i点在路径中的顺序为第L_is个位置，则：

L_is（i+n_）t，i=1，2，…，n，s，t=1，2，…，2n（3）

4算法设计

已知（R₁，R₂，…，R_n）和（T₁，T₂，…，T_n）分别是订单O_i（i=1，2，…，n）的取货点和送货点坐标，由给定坐标可以计算出各点间的距离。

求解目标是优化到达全部取货点（R₁，R₂，…，R_n）和送货点（T₁，T₂，…，T_n）的顺序，使其在满足每订单先取货后送货的前提下，总距离最短。

4.1染色体定义

将（R₁，R₂，…，R_n）編号为（1，2，…，n），（T₁，T₂，…，T_n）编号为（n+1，n+2，…，2n），组合构成（1，2，…，n，n+1，n+2，…，2n）基因染色体。染色体是1到2n的随机排列，但必须满足R_i（i=1，2，…，n）在T_i（i=1，2，…，n）之前。

4.2目标函数

目标函数是染色体所对应排列中各相邻两点间的距离之和，即一条路径的总路程最短。设两点间的距离为c_ij.1≤i，j≤2n。对任一排列i₁，i₂，…，i_2n的总路程为s=c_i1i2+c_i2i3+…+c_{（i2n-1）i2n}。

4.3适应度函数

4.4初始种群

设初始种群大小为P_i，将（1，2，…，2n）随机排列并检验点R_i（i=1，2，…，n）的位置是否都在T_i之前（i=1，2，…，n），符合条件的即为一个有效解。如此得到P_i个有效解，为初始种群。

4.5选择

采用二元竞标法，将种群中的p_i个解随机两两分为P_i/2组，比较每组两个解的适应度，选择适应度大的那个解。重复P_i次，将初始种群的P_i个解替换成适应度相对较大的P_i个解（会有重复解出现）。

4.6交叉

将二元竞标法选择后得到的解两两配对交叉。将解A和解B任选对应的一段基因A^*和B^*进行交叉，将A^*和B^*分别排在B和A的左边，得到A^*B和B^*A，再檢验B和A中与A^*和B^*中重复的点将它们删去，得到两个新的解，并保证每个解中，对全部取货点和送货点不遗漏也不重复。设交叉概率p_C=C。

4.7重组变异

设重组变异的概率p_M=M，应满足：

p_C+p_M=1（4）

重组变异时，将进行交换、逆转和插入。设交换概率p_S=S，逆转概率p_R=R，插入概率p_I=I。应满足：

p_S+p_R+p_I=1（5）

将一个解中任选两点进行如下操作：

（1）交换。交换两点位置。

（2）逆转。将两点间所有点的排列顺序逆转。

（3）插入。将排在左边的点移动到右边点的右边。

4.8选择种群中的最优解

交叉和变异后产生的新排列有可能出现不符合R_i（i=1，2，…，n）在T_i（i=1，2，…，n）之前的前提。因此交叉和变异后都需要检验排列是否是有效解。判断为有效排列后再替换原排列。

4.9循环迭代

种群经过二元竞标，交叉和变异之后得到新的种群。将新种群中个体适应度最大，即种群中最优的解选出得到第一代最优解。将新种群再经上述二元竞标，交叉和变异后得到第二代最优解。

循环迭代上述操作（4.5～4.8）直到没有更优解出现或达到预设上线M次。

具体优化求解流程如图3所示。

5算例分析

图4为3×4个街区组成的服务社区。街道间距单位为1km，即社区南北宽3km，东西长4km。设外卖骑手在某一时间段内，收到了10个订单，即有10个取货点和10个对应送货点，以任一取货点为起点开始求解完成任务的总路程及所需时间。

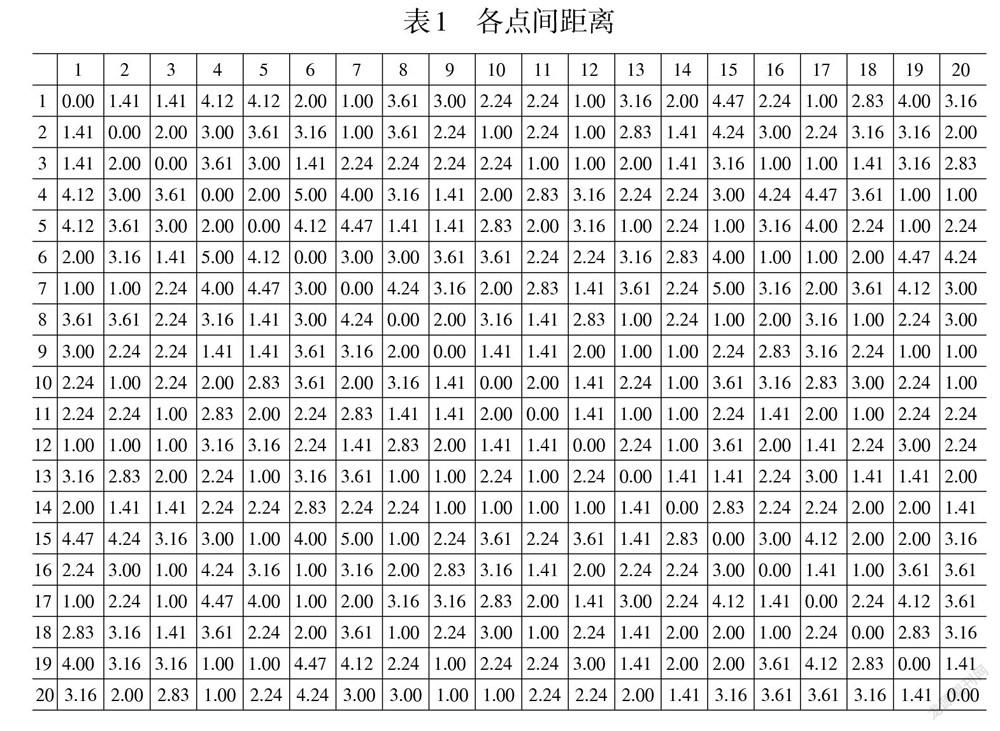
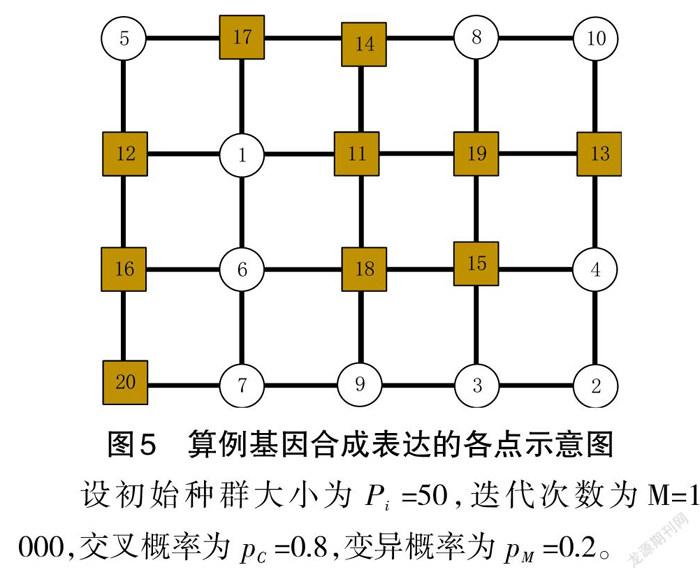
图4中，圆圈（1，2，…，10）为订单（1，2，…，10）的取货点，方框（1，2，…，10）为对应的送货点。为求解方便，取货点用（1，2，…，10）表示，送货点用（11，12，…，20）表示，如图5所小。则构成初始基因染色体种群为（1，2，…，20）。设定最左下角点20的坐标位置为（0，0），合成表达后的（1，2，…，20）各点坐标为：（x，y）={（1，2），（4，0），（3，0），（4，1），（0，3），（1，1），（1，0），（3，3），（2，0），（4，3），（2，2），（0，2），（4，2），（2，3），（3，1），（0，1），（1，3），（2，1），（3，2），（0，0）}，各点间的距离见表1。

设初始种群大小为P_i=50，迭代次数为M=1 000，交叉概率为p_C=0.8，变异概率为p_M=0.2。

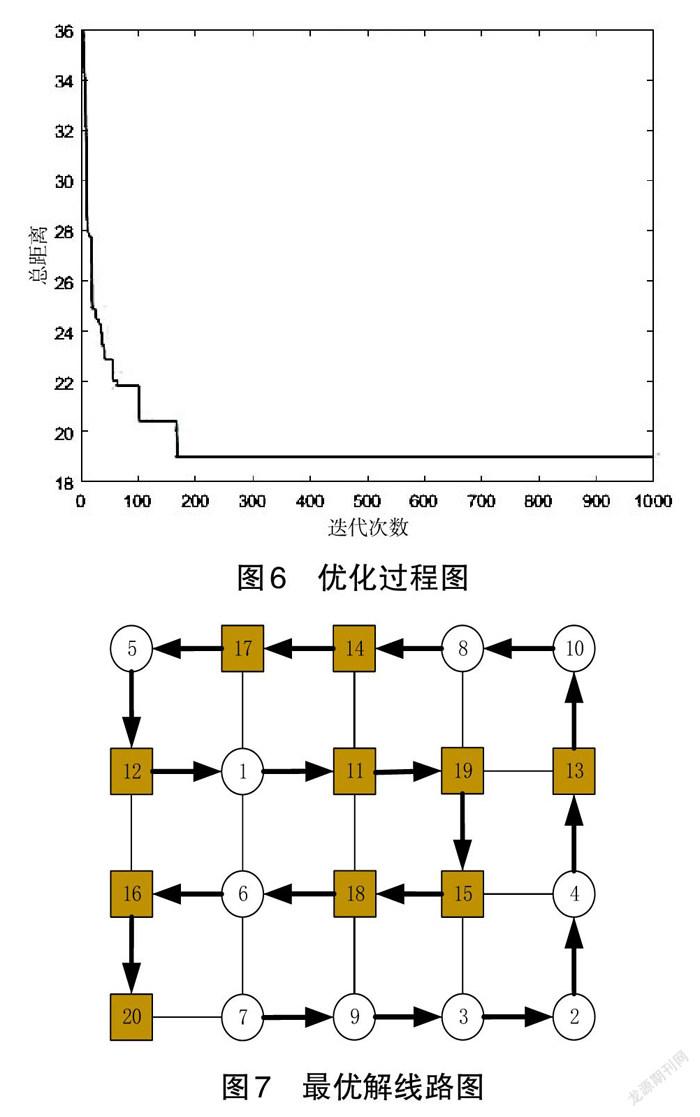
按“算法设计”的流程求解，求解迭代过程如图7 所示，求得最优路线图如图8所示，最佳里程为19。

最优解路径顺序为：

7（取货）→9（取货）→3（取货）→2（取货）→4（取货）→13（目标3送货）→10（取货）→8（取货）→14（目标4送货）→17（目标7送货）→5（取货）→12（目标2送货）→1（取货）→11（目标1送货）→19（目标9送货）→15（目标5送货）→18（目标8送货）→6（取货）→16（目标6送货）→20（目标10送货）

假设快递员平均时速20km，则需要大约57min，即一个小时以内可完成10个订单配送，满足一个小时完成全部订单的目标要求。

本算例没有考虑到实际取送货时的等待时间，但设每个街区街道间距为1km，10个订单覆盖3×4=12km²的社区，其服务距离超过实际服务范围，所求解有一定的可信度。

考虑两个极端情况作为对照：（1）当外卖骑手按照顺序将外卖订单全部取完再送，则总路程为49.3，总时间约需要150min。（2）如果按照取一个送一个的顺序，总路程为44.9，总时间需要约135min。由此可见，使用本算例采用的算法给出的优化解极大地缩短了配送时间，可大大提高配送效率、节约人力成本。

6结语

在第三方外卖平台兴起之前，一部分餐馆也为临近的客户提供送餐上门服务。这种情形类似于一个配送中心（即餐馆）和多个配送目的地，与VRP的模型描述相近。现在的第三方外卖服务平台往往要服务庞大数量的外卖供应商和客户。现有研究不论是关于VRP的还是TSP的，都与现实情况有一定程度的差异，并不能很有效的解决现实中的外卖配送问题。本文梳理外卖服务特征，提出了无中心多点到多点配送建模与求解方案。所提思路在保障外卖服务要求的前提下，实现了最优路径的求解。在实施路径优化的过程中，在保证每单“先取后送”，每组订单不必“先取先送、后取后送”的前提下，优化路径的同时也实现了订单取货顺序的优化。算例证明可以有效提高工作效率，保障服务水平。

本文所考虑的情形还相对简单，未来会考虑带时间窗限制条件下多车协同完成的调度和路径规划等更复杂情况下的建模，也会利用更先进的智能算法来求解。

[参考文献]

[1]艾媒咨询.外卖行业数据分析：2020年中国外卖行业市场规模达6 646.2 亿元[EB/OL].（2021-04-13）[2021-10- 08].http：//k.sina.com.cn/article_1850460740_6e4bca440_ 2000sqad.html.

[2]赖祐萱.外卖骑手困在系统里[EB/OL].（2020-09-08）[2021- 10-08].https：//baijiahao.baidu.com/s？id=1677231323622016633_&wfr=spider&for=pc.

[3] DANTZIG G B，RAMSER J H.The Truck Dispatching Problem[J].Management Science，1959，6（1）：80-91.

[4] SAVELSBERGH M.Local search for routing problem with time windows[J].Annals of Operations Research，1985，2（3）：285-305.

[5]徐倩倩.考虑商家出餐时间的外卖路径优化[D].上海：东华大学，2021.

[6] He Y，Hui C- W.A binary coding genetic algorithm for multi-purpose process scheduling：A case study[J].Chemical Engineering Science，2010，65（16）：4 816-4 828.

[7] ARCHETTI C，SPERANZA M G，Hertz A.A Tabu Search Algorithm for the Split Delivery Vehicle Routing Problem[J]. Transportation Science，2006，40（1）：64-73.

[8] GAMBARDELLA L M，DORIGO M.An Ant Colony System Hybridized with a New Local Search for the Sequential Ordering Problem[J].INFORMS Journal on Computing，2000，12（3）：237-255.

[9]BRAYSY O，et al.An Effective Multirestart Deterministic Annealing Metaheuristic for the Fleet Size and Mix Vehicle- Routing Problem with Time Windows[J].Transpotation Science，2008，42（3）.

[10] MAKINO Y，FURUTA K，KANNO T.Interactive Method for Service Design Using Computer Simulation[J].Service Science，2009，1（2）：121-134.

[11] ANDREAS A K，SMITH J C.Mathematical Programming Algorithms for Two- Path Routing Problems with Reliability Considerations[J].INFORMS Journal on Computing，2008，20（4）：553-564.

[12] LAI H C，NAKAGAWA T，MUROGA S.Redundancy check technique for designing optimal networks by branch- and- bound method[J].International Journal of Computer & Information Sciences，1974，3（3）：251 -271.

[13] GOUNARIS C E，WIESEMANN W，FLOUDAS C A. The Robust Capacitated Vehicle Routing Problem Under Demand Uncertainty[J].Operations Research，2013，61（3）：677- 693.

[14] Erera A L，MORALES J C，SAVELSBERGH M. The Vehicle Routing Problem with Stochastic Demand and Duration Constraints[J].Transportation Science，2010，44（4）：474-492.

[15] Solomon M M，J Desrosiers. Time Window Constrained Routing and Scheduling Problems[J].Transportation Sci- ence，1988，22（1）：1-13.

[16]徐興，钱誉钦，赵芸，等.基于改进蚁群算法的立体仓库三维空间路径优化[J].计算机集成制造系统，2021，27（1）：206-213.

[17]王文杰，孙中苗，徐琪.考虑社会配送供应能力的众包物流服务动态定价模型[J].管理学报，2018，15（2）：293-300.

[18]方婷.众包物流的风险与对策：以三家众包物流平台为例[J].中国管理信息化，2018，21（23）：151-152.

[19]李玉，吴斌，王超.基于前景理论的众包物流配送方行为决策演化博弈分析：基于发货方视角[J].运筹与管理，2019，28（6）：129-135.