基于三角函数求导的科里奥利力表达式推导
2021-09-12杨照锐何尚文
杨照锐 何尚文


[摘 要] 理论力学中,科里奥利力是非常重要且相对抽象不容易理解的教学内容。利用旋转坐标中做匀速直线运动物体的相对运动,通过向量在直角坐标系下的描述以及三角函数求导,用数学的概念描述了科里奥利力的产生,并根据向量方向的特征解释了科里奥利力方向的判断。能够使学生更加清晰地认识科里奥利力的同时深度理解高等数学在实际力学中的应用,培养学生更加严密的数理逻辑能力。
[关 键 词] 科里奥利力;动参考系;三角函數求导
[中图分类号] G642 [文献标志码] A [文章编号] 2096-0603(2021)28-0068-02
科里奥利力(下文简称科氏力)是当动参考系发生旋转的同时质点相对于动系有相对运动而产生的惯性力,它是大学物理和力学专业课程中的重要组成部分[1]。在点的运动合成中,动系的转动且质点有相对速度的运动状态比动系平移的情况要复杂而抽象,学生往往难以理解。同时科氏力方向的判断给很多学生造成很大的困扰[2]。尽管对于科氏力在生活和工程中应用的探讨和研究有很多,但是用较为严密的数学理论对科氏力的产生进行推导的讨论尚不多见[3][4]。基于此,本文通过使用大学数学中最基本的坐标变换和三角函数求导对科氏力的产生进行数学描述。采用该方法的讲解能够加深学生对低年级阶段学习的高等数学在实际力学问题中应用的理解,更深入地理解科氏力。
一、旋转坐标系中匀速运动的物体运动方程
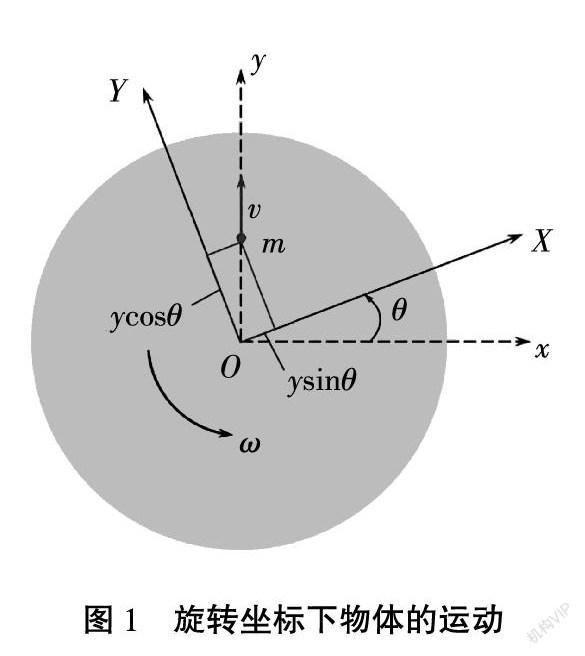
图1中圆盘以匀角速度ω沿逆时针方向旋转,xy坐标系为惯性系,XY系为随圆盘一起转动的随体坐标系。质量为m的物体不受任何外力的情况下在圆盘上做匀速直线运动,速度为v。当物体的运动方向沿惯性系的y轴时,在xy坐标下该物体的位置向量■和速度分别表示为
三、总结
从旋转坐标系下匀速运动的物体运动方程,通过三角函数求导给出了在运动方程中科里奥利力的数学表达式。进一步分析了科氏力的大小和方向。本文通过高等数学中的一些基本的概念和方法,对科氏力进行了详细的描述。既有数学的严密,又具备力学的深刻,使相对较为抽象的概念能够清晰地呈现。教学中使用该方法能够使学生更好地理解数学的基本思想在力学中的应用,培养学生更加缜密的数理逻辑推导能力,增加对力学概念的更深刻认识。
参考文献:
[1]漆安慎,杜婵英.普通物理学教程:力学(第三版)[M].北京:高等教育出版社,2012.
[2]陆天明.关于地转偏向力问题的讨论[J].物理之友,2020(36):5-6.
[3]哈尔滨工业大学理论力学教研室.理论力学(I)第8版[M].北京:高等教育出版社,2016.
[4]邹越,王惠敏,黄韵瑾,等.科里奥利力几种常见错误认识的解析[J].物理通报,2016(1):5-8.
◎编辑 司 楠
