粉砂地层中列车载荷对曲线隧道沉降的影响

肖昭然，王永刚，张文萃，任 磊

（1.河南工业大学 土木工程学院，河南 郑州 450001；2.郑州地铁集团有限公司 技术管理部，河南 郑州 450000）

0 引言

盾构隧道长期沉降严重影响地铁正常运营和结构安全[1]，其影响因素多且复杂，其中地铁列车运行产生的振动载荷是一项重要因素[2].如上海地铁一号线在地铁开通运营后，穿越砂土层的某区间地铁隧道沉降量大于其他区段[3].

目前针对列车振动载荷作用下曲线盾构隧道周围土层动力响应和长期沉降问题常用的方法有：现场实测、室内试验、数值模拟和理论计算.现场实测方面，袁扬[4]等通过现场实测分析了曲线段地铁隧道引起地面振动的传播规律.室内试验方面，YANG[5]等利用室内缩尺试验模型分析衬砌不同的连接方式下长期列车载荷对土体的动力响应.数值模拟方面，HUANG[6]、高广运[7]、苏丽娟[8]等通过建立数值模型对隧道下方土层的长期沉降和动力响应进行了研究.理论计算方面，吕玺琳[9]基于黄茂松[10]提出的土体累积应变模型，将交通载荷简化成静力载荷，结合室内试验来预测路基在交通载荷作用下的长期沉降.现有文献中多以提出一种沉降计算方法或建立数值模型进行计算，没有充分的监测数据与计算结果进行验证.因此结合现场实测和数值模拟分析是研究此类问题的有效方法.

尽管诸多学者对列车循环载荷作用下地铁隧道沉降做出了大量研究工作，但是大多数研究以直线隧道作为研究对象，曲线隧道的相关研究较少，而实际工程中曲线隧道非常常见，因此对列车载荷作用下的曲线隧道动力响应研究十分必要.

以郑州地铁一号线一期工程为背景，对隧道结构进行现场实测.将作用在轨道上的列车载荷分解为竖向力、横向力、轨道超高引起的离心力，将横向力沿隧道轴线径向施加在隧道道床上，结合固结工况和列车振动载荷计算工况，研究粉砂土层中不同转弯半径和车速下对曲线隧道周围土层动力响应和沉降的影响，总结其中规律，以期为类似工程提供参考和建议.

1 现场实测分析

1.1 工程概况和测点布设

本次监测区域位于农业南路-东风南路站区间，隧道先后穿越粉砂和粉土地层，该区段隧道埋深15～20 m，隧道直径为6 m，隧道管片厚度为0.30 m.

各测项点位在隧道内的空间位置关系见图1.道床竖向位移5 个断面（RC32～RC36），衬砌结构收敛测点2 个断面（RS16 1-4～RS17 2-3）.

图1 隧道监测点位布设示意Fig.1 schematic diagram of tunnel monitoring points

1.2 现场实测分析

（1）道床竖向位移监测结果分析

图2、图3 分别是隧道下行线在K29+358.74～K29+477.74 区段的连续多期沉降变化量和累积沉降曲线，X轴代表监测时间，Y轴代表位移，由图2可知变化量最小值监测点位 RC32 在第 3 期0.77 mm，变化量最大值监测点位RC33 在第4 期-8.78 mm，这是因为监测区段附近有较大的深基坑工程进行施工.其余各测点每期变化量都较稳定.对比图2、图3 可知隧道在列车振动载荷的长期作用下整体呈现下沉趋势.

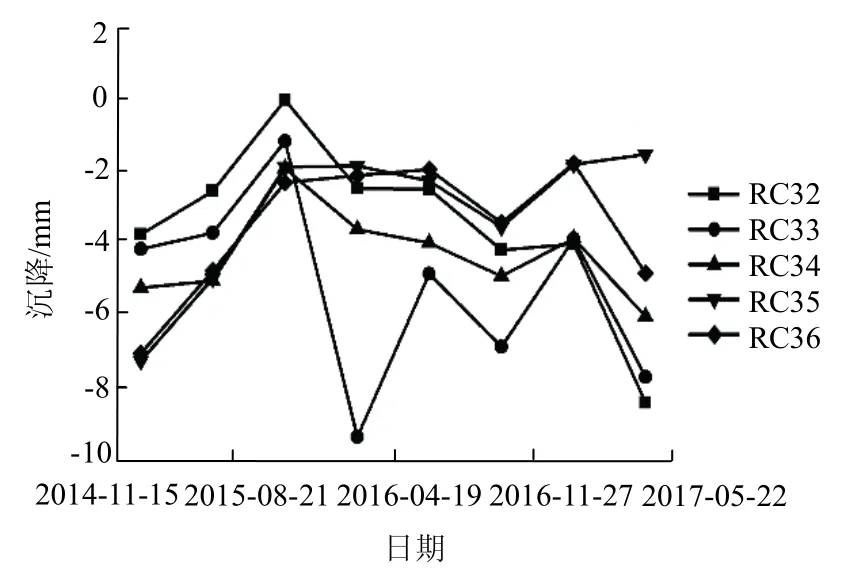
图2 农业南路站-东风路站各期沉降变化量Fig.2 amount of settlement variation in nongye south road station-dongfeng road station

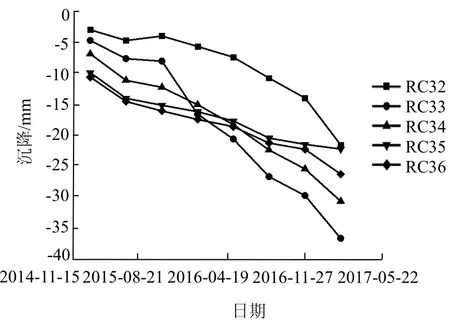
图3 农业南路站-东风路站各期累积沉降变化量Fig.3 cumulative settlement variation of nongye south road station-dongfeng road station

现场实测道床竖向位移包含了隧道盾构施工、列车振动载荷、工后固结、区域性地面沉降和隧道结构变形等多种因素的影响.由于现场实测初始值是在隧道建成后进行的，所以本文不考虑因隧道施工引起的沉降；采用相对沉降分析，不考虑区域性地面沉降的影响，第1 期现场实测完成距离隧道盾构施工约1 年，隧道周围土层工后固结尚未完成.因此，认为现场实测累积沉降值为列车振动载荷和工后固结两种因素之和.数值模拟设置工后固结和列车振动载荷计算工况.保留工后固结工况计算结果应力场，在此基础上进行列车振动载荷的计算，将计算得到的土层应力结果用于理论计算，对比分析现场实测结果验证模型建立的准确性.

（2）衬砌结构水平和收敛位移结果分析

图4 是衬砌结构收敛位移随时间的变化曲线，可知衬砌结构收敛最大位移为2.6 mm，满足规范变形要求.由此表明隧道结构变形不是导致累积沉降值增加的主要原因.

图4 各期收敛位移变化量Fig.4 variation of convergence displacement in each period

2 计算模型的建立及列车载荷的施加

2.1 计算模型的建立

曲线隧道在水平方向距离隧道轴线50 m 范围内，水平向振动强度是竖向振动强度的2～4 倍[4].模型X方向，从隧道轴线分别左右两边延伸90 m；模型Y方向，即地铁列车行进方向，取120 m，并在道床上每隔30 m 设置1 个测点，共计5 个测点，测点编号为C1～C5；Z方向表示深度方向取68.3 m.三维数值模型见图5.土体本构关系采用Mohr-Coulomb 弹塑性屈服准则[11-13]，衬砌及道床采用弹性本构关系.

图5 三维数值模型Fig.5 3D numerical model

同时为了节约计算资源，又尽可能地保证数值模拟的准确性，根据工程勘察资料，将研究范围的土体按土层厚度加权平均简化成7 层，以此作为数值模型的土层参数，见表1.

表1 土层物理力学参数Tab.1 physical and mechanical parameters of soil layer

本文采用有限元软件MIDAS 建立地铁道床-衬砌-土体耦合系统的三维动力模型.有限元计算分为2种工况，工况1：对曲线隧道三维模型进行固结计算；工况2：在固结计算的基础上进行列车移动载荷的动力分析，将有限元计算结果与经验拟合公式相结合，通过计算的累积沉降值与现场实测累积沉降值进行对比，验证数值模型的准确性，进而计算不同转弯半径和不同车速下的隧道长期累积沉降.

2.2 列车载荷的施加

把作用在轨道上的载荷分成列车轴重引起的竖向力和横向力、轨道超高引起的离心力[14]，其受力分析见图6.

图6 曲线段轨道受力分析Fig.6 curved track stress analysis chart

受力分析公式为

式中，Fz、Fx分别为列车移动载荷作用于曲线轨道的垂向力和横向力，kN；G=mg（m，kg；重力加速度g 取9.81 m/s2）.

郑州地铁1 号线线路采用国产B 型列车[15].根据地铁设计规范GB50157-2013 获得列车的轴间距和轴载荷，列车运行时速V为80 km/h，这里考虑列车满载乘客的情况.

结合MIDAS 中载荷子程序列车动力载荷模块.由程序生成列车时程载荷见图7.这里只展示隧道转弯半径R为350 m 时间5 s 的列车移动载荷时程曲线.并在模型中同时施加竖向和横向的列车时程载荷，其中横向载荷的作用方向是沿着隧道轴线径向逐渐变化的，载荷在模型中的施加见图8.

图7 列车移动载荷Fig.7 train moving load time history

图8 载荷施加示意Fig.8 schematic of load application

3 计算结果分析

3.1 隧道底部土体动力响应

首先对有限元数值模拟结果进行分析，分析列车振动载荷运行1 次后，在不同隧道转弯半径和行车速度下隧道底部土体动力响应随深度的变化规律，以此确定列车振动载荷在土体中的主要影响范围，测线布置见图9.

图9 测线布置示意Fig.9 schematic of measuring line

（1）不同转弯半径下隧道底部振动传播规律

图10 是列车运行时速V为80 km/h 时隧道下方土体在不同转弯半径R下动力响应结果.

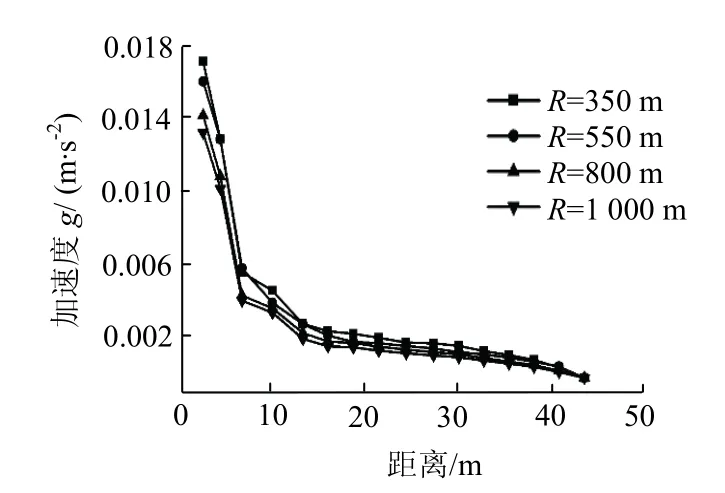
图10 测线1 在不同转弯半径R 下各测点的加速度Fig.10 acceleration of each measuring point of measuring line 1 under different turning radius

由图10 可知，在竖直方向不同的转弯半径下列车运行引起隧道下方土体的加速度幅值都是在紧贴隧道衬砌位置加速度最大，随着与隧道底部距离的增加而逐渐减小，直至模型边界处降至最低.振动在向下传播过程中在距离隧道底部0～15 m 内加速度衰减很快，其中R=350 m 加速度从距离隧道底部0 m 处0.017 m/s2减少到15 m 处的0.003 m/s2，加速度减少82.4%，R=550 m、R=800 m、R=1 000 m动力响应减小幅度分别为81.8%、82.9%和84.0%，由此可以确定列车振动载荷对隧道下部土体的主要影响范围.

（2）不同车速下隧道底部振动传播规律

图11 是列车在不同的行车速度V下隧道底部土体加速度变化曲线.

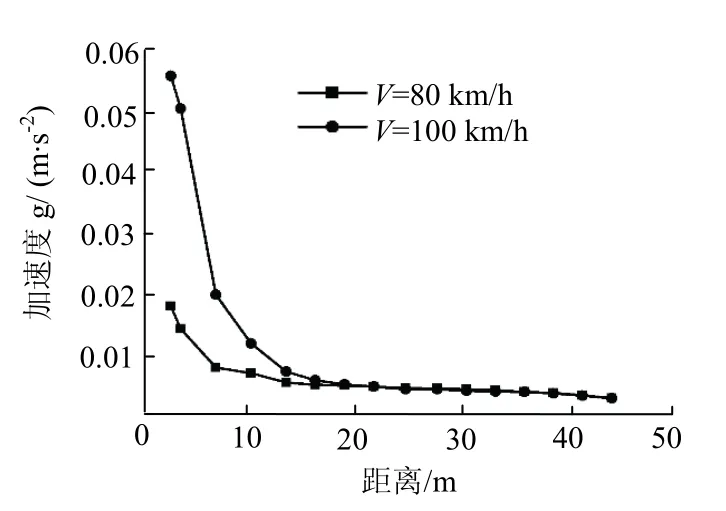
图11 测线1 在不同车速下各测点的加速度Fig.11 acceleration of measuring line 1 at each measuring point under different vehicle speeds

由图11 可知当列车运行速度由V=80 km/h 提升到100 km/h 时隧道下方土层动力响应增加71.4%，2种车速下对隧道下方土层的主要影响在0～15 m，当距离隧道底部大于15 m 时二者加速度大小和变化趋势基本趋于一致.

4 隧道长期沉降计算

4.1 计算结果与实测结果对比

采用LI[16]对MONISMITH[17]修正后的指数模型，隧道长期沉降计算模型见式（4），其中a、b、m参数取值与土的类型有关，LI[16]给出几种土的取值范围.

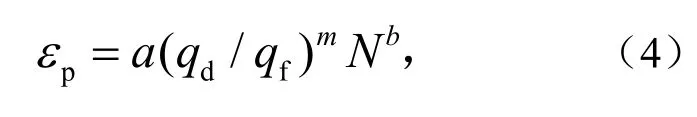
式中，qd、qf分别为土体动偏应力和土体静强度，kPa，计算过程见文献[18].

固结工况计算时长和列车具体运行次数根据列车开始运营日期至第8 次监测日期来确定，若按列车年运行次数为42 万次[19]，通过对固结工况和列车振动工况进行计算，结合理论公式计算出的沉降值与现场实测数据进行对比进而修正计算模型参数，最终得到a=0.83、b=0.13、m=2.12；累积沉降计算结果与现场实测结果对比，见图12.

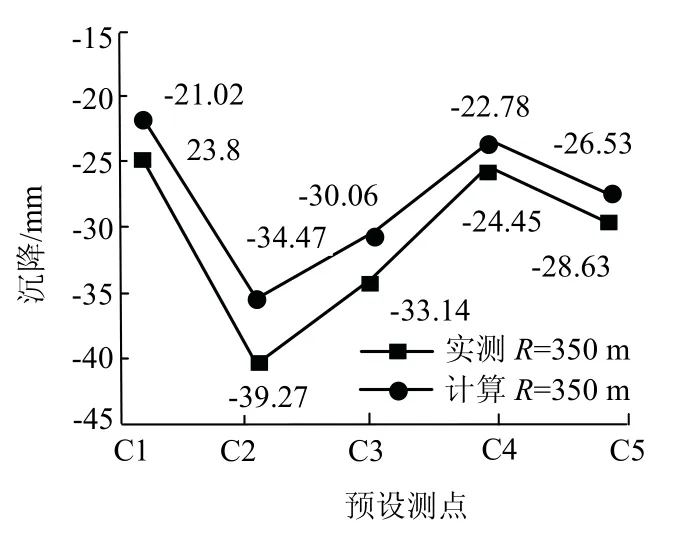
图12 理论计算与现场实测沉降值对比Fig.12 comparison between theoretical calculation and actual measured settlement

由图12 可知，现场实测累计沉降值与理论计算结果较为接近，且平均相对误差绝对值为9.47%，在合理范围内，证明本文曲线隧道列车载荷的加载方式可行.但本文理论计算结果略小，原因可能是数值模型采用单洞单线隧道结构，而实际工况为双洞单线隧道结构.

4.2 不同转弯半径下计算隧道沉降值对比

图13 为地铁隧道不同转弯半径下计算累积沉降值对比曲线，随着隧道转弯半径的增大，最大累积沉降值分别降低8.4%、10.8%和14.6%.其原因是随着隧道转弯半径的增加，施加在道床上的横向时程载荷在逐渐的减小，导致对隧道下方土体的影响有些减弱.

图13 不同转弯半径理论计算沉降值对比Fig.13 comparison of settlement values calculated by different turning radius theories

4.3 不同车速下计算隧道沉降值对比

由图14 可知当列车时速V=100 km/h 时计算得出的沉降值比时速V=80 km/h 时略小.而由图11 可知提高列车运行速度会引起隧道下方土体振动响应有所增加，但对应的隧道下方土体沉降确稍有降低，这是因为提升速度，载荷变化快，载荷在同一位置作用的时间减少，使得土体的变形减小.

图14 不同车速理论计算沉降值对比Fig.14 comparison of settlement values calculated by different speed theory

5 结论

（1）通过对郑州粉砂地层中运营的曲线地铁隧道进行现场实测，实测结果表明隧道衬砌结构变形最大值为2.6 mm，说明隧道结构变形不是引起隧道累积沉降的主要原因.

（2）粉砂土层中地铁列车移动载荷作用下的曲线隧道，底部土体的动力响应随着深度和转弯半径的增加而减小，动力响应的主要影响范围在隧道底部0～15 m.

（3）隧道下方土层动力响应和长期累积沉降随着隧道转弯半径的增加而减小；在隧道相同的转弯半径下，列车由常规时速增加到较快时速时，引起隧道下方土层动力响应增加71.4%，与之对应的累积沉降值降低6.4%.