小半径曲线盾构施工对周边土体位移的影响

吴 迪，蒋敏敏，肖昭然

（河南工业大学 土木工程学院，河南 郑州 450000）

0 引言

城市地铁隧道线路线型的设计，受到地上及地下建构（筑）物的制约，隧道的部分区段常设计为小半径曲线.小半径曲线盾构施工不同于直线盾构隧道，由于盾构机姿态偏转、曲线内侧土体超挖、千斤顶不平衡推力等因素的影响导致地层不均匀扰动、土体变形复杂、对临近建（构）筑物产生危害等.因此，结合工程实测数据，建立小半径曲线盾构施工数值模型，对研究土体变形的复杂规律，具有重要理论指导与实践意义.

近年来，关于盾构隧道施工引起的土体位移变化规律，国内外专家学者进行一系列的研究.晁峰[1]等通过现场原位试验研究了盾构施工对板岩地层的扰动规律.虞兴福[2]等通过实验性监测研究了盾构掘进过程中对周边土体的影响范围及变形规律.姜忻良[3-4]等推导出计算任一土层深度竖向位移公式，将数值模拟与实测数据相结合，总结了盾构推进至不同阶段时隧道周边土体两相位移的变形规律.王占生[5]等结合MAIR[6]等的研究，提出深埋隧道盾构施工造成的深层土体沉降与水平变位的预测方法，文献[7]～文献[10]也进行了相关研究.王国富[11]等通过多影响因素的定量分析与定性评价，研究曲线盾构隧道埋深、盾构直径、曲率半径和千斤顶不平衡推力对地表沉降的影响规律.路林海[12]等基于公式Peck[13]与实测数据，推导出曲线盾构施工引起地表沉降的修正Peck 公式.周舟[14]以实际工程为例，介绍了曲线盾构引起的轴线预偏、地表沉降和管片错台渗漏水等情况的控制措施.黄雪梅[15]等总结了小半径曲线盾构隧道下穿铁路时引起的地层沉降的控制措施.李强[16]等研究了盾构机盾构机抬头、叩头及曲线掘进时引起的地表沉降规律.

基于上述文献分析可知，目前对于盾构隧道施工引起的周边土体位移主要集中于常规隧道线型，而针对小半径曲线盾构施工引起周边土体位移变化规律的研究相对较少，尤其综合考虑管片折减、等代层厚度、注浆层凝固过程和千斤顶不平衡推力等因素的曲线盾构施工全过程模拟分析较少，但随着地铁建设的日益增加，小曲线盾构隧道也将越来越多.因而，本文以郑州粉土地层某地铁线路小半径曲线盾构施工为背景，通过分析实测数据研究隧道周边土体的位移规律，将其与直线隧道进行对比；运用Midas 软件对小半径曲线盾构施工进行全过程模拟，将实测数据与有限元计算结果对比分析以得到更为可靠的土体变形规律；并探究隧道曲率半径和千斤顶不平衡推力比对土体位移的影响，给类似工程的设计和施工以指导作用.

1 工程实测分析

1.1 工程概况

郑州某地铁隧道盾构施工小半径曲线段长为469.21 m，取单条隧道即隧道左线进行研究，曲率半径为300 m.隧道拱顶埋深为10.95 m，穿越段地质情况以粉质黏土和粉土为主，采用主动铰接土压平衡盾构机，主机长约为 8 m，开挖直径6 480 mm，管片环宽1.2 m，外径6 200 mm，内径5 500 mm，厚度350 mm，转弯管片的楔形量为37.2 mm，双面楔形.

1.2 测点布设

地表沉降共布设5个监测断面，每个断面有15个地表沉降测点，编号为DB1-1～DB5-15，断面间距为20 m，测点间距3 m；土体深层水平位移共布设2 个测点，用CX1、CX2 表示，其分别位于隧道曲线外、内侧，与隧道水平间距为0.9 m.测点间距和位置见图1.

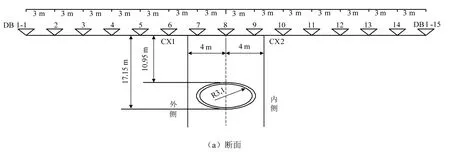
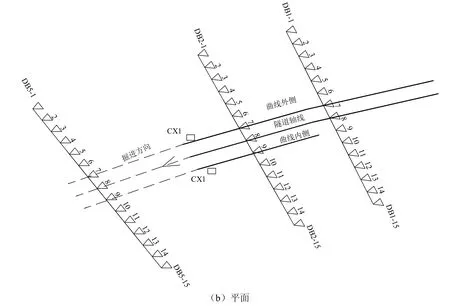
图1 监测点布置Fig.1 layout of monitoring points

1.3 实测数据分析

（1）地表沉降

横向地表沉降见图2.

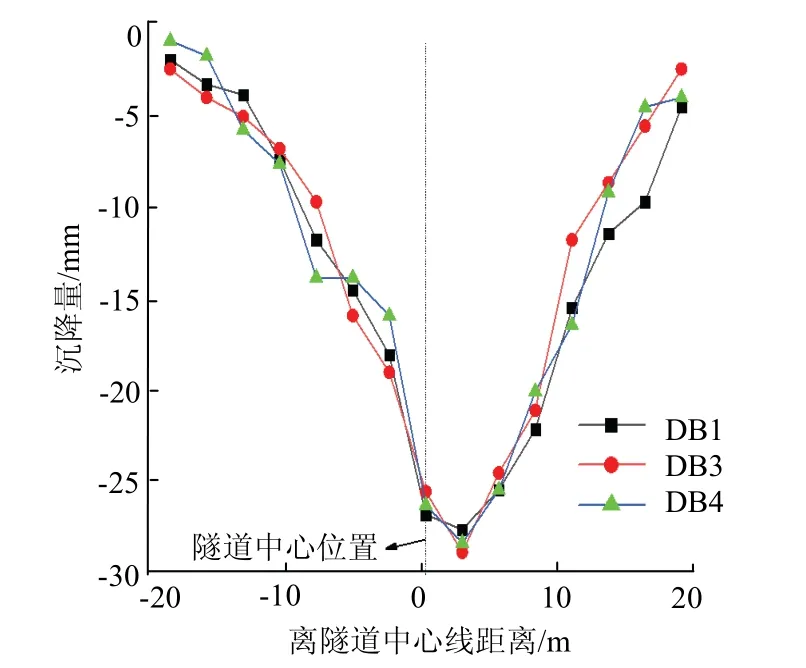
图2 横向地表沉降Fig.2 lateral surface subsidence

由图2 可知，横向地表沉降槽近似符合高斯正态分布.通常而言，盾构施工引起的地表沉降最大值位于隧道轴线正上方，而现场监测结果显示盾构施工引起的地表沉降最大值位置向隧道曲线内侧偏移，且基本位于隧道曲线内侧边线上方.究其原因，盾构在曲线段掘进时，通过外侧千斤顶推力和油缸行程差大于内侧而实现盾构机偏转，同时刀盘对曲线内侧土体进行超挖，进而引起地表沉降最大值向曲线内侧偏移，因此分析盾构隧道的曲率半径和盾构外侧与内侧的顶推力比，有利于明确地表沉降最大值向隧道曲线内侧偏移的机理.尽管盾构姿态调整过程中引起土体超挖导致地层扰动加剧，但地表沉降量仍在可控范围之内，3个监测断面的最大地表沉降量为28.6 mm，其未超出规范规定的30 mm.

（2）土体水平位移

图3、图4 分别为刀盘距离测斜孔CX1、CX2不同距离时的土体横向水平位移曲线，横轴正值表示位移朝向隧道方向，负值表示位移远离隧道.

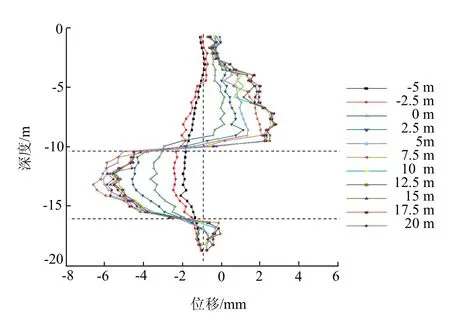
图3 外侧测斜CX1 水平位移Fig.3 lateral CX1 horizontal displacement

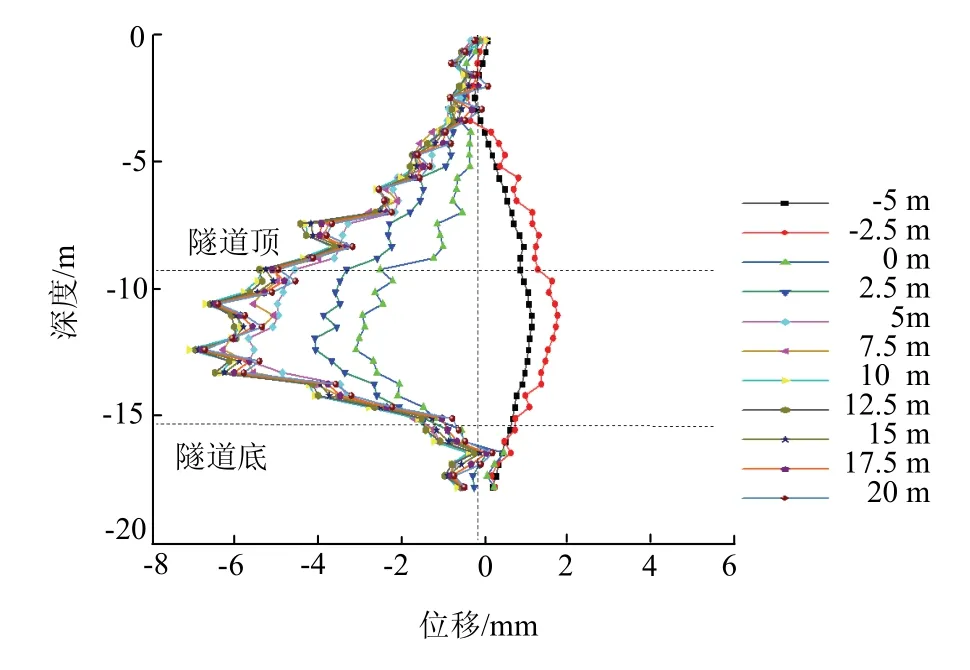
图4 内侧测斜CX2 水平位移Fig.4 inside CX2 horizontal displacement

①曲线外侧土体位移规律

由图3 可知，隧道顶部以上土体位移趋势与隧道范围的土体变形差异明显，顶部以上土层由于盾构掘进引起的地层损失，水平位移主要朝向隧道方向，而隧道范围内的土层受盾构转弯的挤压作用，位移朝向隧道外侧，这与普通直线盾构隧道的变化规律基本一致[7].

隧道拱顶以上土体在刀盘接近过程中变形很小，其位移主要发生在盾构通过阶段和盾尾离开阶段，盾构通过时土体应力释放，盾壳对土体摩擦造成剪切扰动，位移朝向隧道方向不断增大，最大位移为3.72 mm，发生在刀盘到达7.5 m 处（盾尾即将脱离测点），盾尾脱离后，土体向盾尾空隙填充，变形继续发展，最终被注浆体控制，在刀盘通过测点 20 m 后趋于稳定.最大变形为4.53 mm，发生在埋深7.05 m 处，与隧道拱顶垂直间距为3.9 m.

隧道范围内土体，在刀盘接近测点过程中，受盾构推力影响，向外侧排开，刀盘到达-2.5 m 时位移最大为-1.68 mm，盾构通过测点过程中，受盾壳挤压作用，位移朝向隧道外侧持续增大，在盾尾即将脱出时（刀盘到达7.5 m 位置）位移最大为-6.68 mm，盾尾远离测点后土体填充建筑空隙，位移朝向隧道方向，但很快被注浆体控制，变形趋于稳定，最终位移最大为-5.55 mm，发生在埋深13.79 m 处，与隧道轴线的垂直距离为 1.11 m.水平最大位移基本发生在隧道中部[5,8,17].

隧道底部1～2 m 的土体于各阶段的变形都很小，位移在0.43～1.13 mm.

② 曲线内侧土体位移规律

由图4 可知，随着刀盘接近、通过并远离测点，曲线内侧土体经历了先挤压后应力释放的过程，在刀盘到达测点前-5～0 m，土体受到盾构推力挤压作用，向远离隧道方向移动，刀盘到达-2.5 m 时位移最大为-1.73 mm；随后刀盘开挖至0 m 位置（即刀盘开挖至测点处），土体卸荷扰动，向隧道方向位移，位移最大为2.65 mm；在盾构机通过测点过程中，因为曲线内测刀盘超挖，隧道范围土层产生更大的建筑空隙，导致土体朝向隧道的位移继续增大，刀盘到达7.5 m 时，位移最大为5.76 mm，此后盾尾离开测点，土体失去盾壳支撑，同步注浆和凝浆液固不及时，土体挤入盾尾空隙，变形达到6.28 mm；随着盾构远离测点，在同步注浆浆液硬化后，水平位移趋于稳定，在刀盘到达20 m 时，位移最大为5.93 mm.

整体来看，隧道曲线内侧土体位移主要集中在隧道所处的土层范围内，即埋深10.95～17.15 m为隧道拱顶埋深至隧道底部埋深，隧道顶部以上土体随着埋深的减小，位移逐渐减小.

2 基于Midas 软件的数值模拟

2.1 Midas 软件建立模型

考虑尺寸效应的影响，模型X方向取约11 倍洞径，即在隧道左右两侧向X轴正负方向各延伸5倍洞径，Y方向为隧道掘进方向，总长度取约10倍洞径，Z方向取约2 倍隧道轴线埋深，故模型尺寸为70 m×60 m×35 m（X×Y×Z），模型边界条件，采用模型四周约束水平方向位移，底部约束X、Y、Z方向的位移，上表面为自由边界.有限元计算模型见图5.

图5 有限元计算模型Fig.5 finite element calculation model

2.2 模型参数选取

模型中盾壳、管片结构及等代层均采用实体弹性模型，土体采用Mohr-Coulomb 弹塑性模型.根据工程勘察资料，各土层参数见表1.

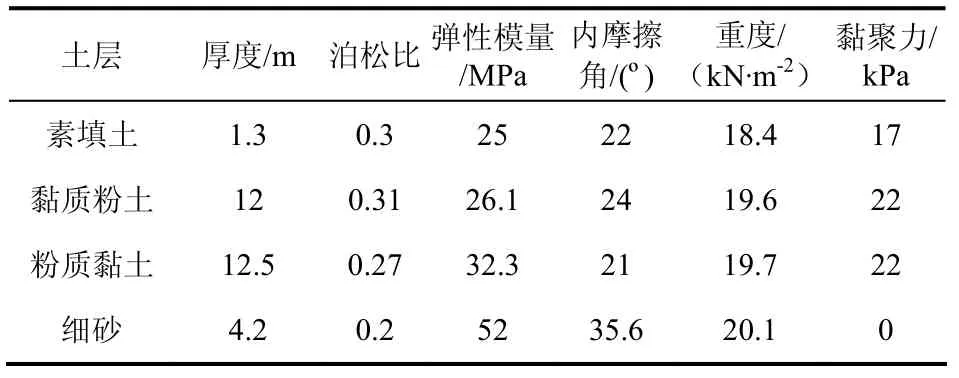
表1 土体物理力学参数Tab.1 soil physical and mechanical parameters

2.3 曲线盾构施工模拟

（1）千斤顶推力分组

根据盾构机参数，盾尾千斤顶推力分组见图6，在曲线段掘进时，保持B 组、D 组推力相等，调节A 组与C 组的推力差实现盾构机转弯.

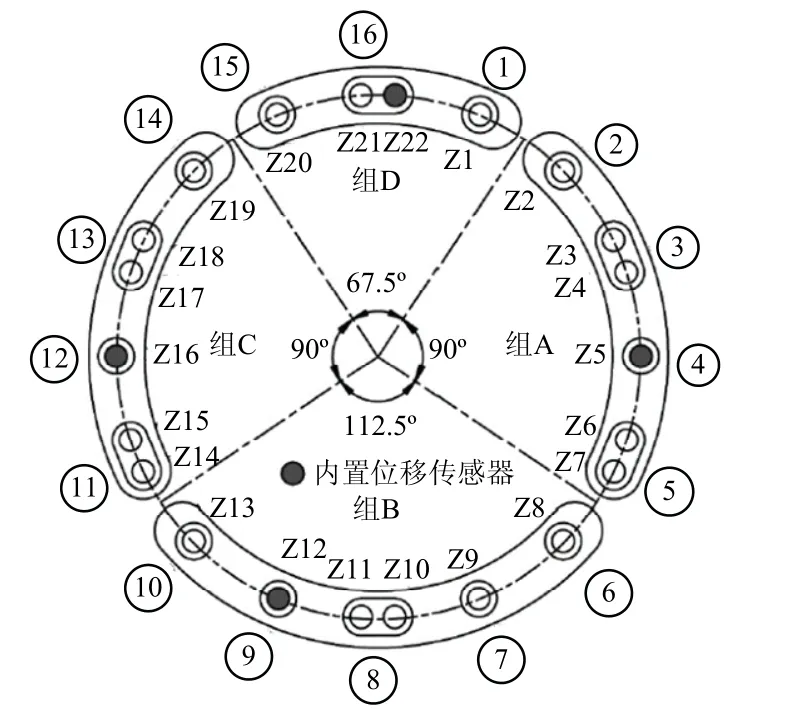
图6 千斤顶推力分组Fig.6 jack thrust grouping

图7 将开挖面沿中轴线等分为左右两部分，各部分分别施加均布压力，以模拟盾构施工时的开挖面不平衡推力，左右侧推力分别用q1、q2表示.

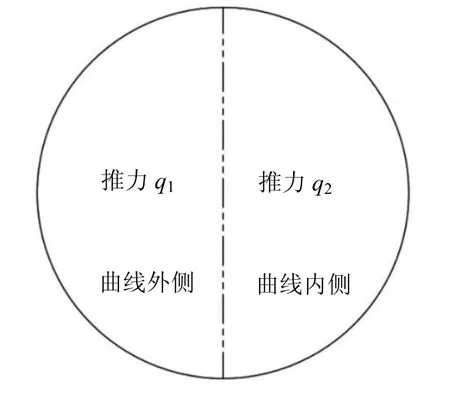
图7 开挖面推力分区Fig.7 thrust section of excavation face

（2）不同厚度等代层模拟

盾构机曲线掘进时，刀盘对曲线内侧土体超挖，以实现盾构机姿态偏转，隧道不同曲率半径时，对线路内侧土体超挖量[18]计算式为

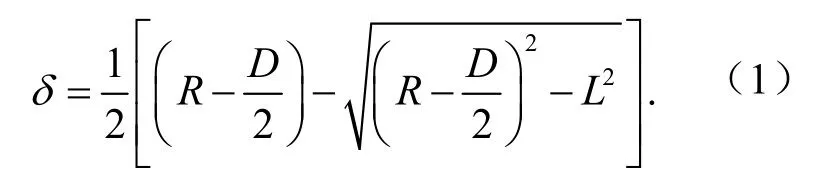
式中，δ为曲线内侧超挖量，mm；R为线路曲率半径，m；D为管片外径，mm；L为盾构机长度，mm，盾壳具有铰接装置的可适当折减.

对于装配式管片，按照均质圆环结构进行模拟[19]，环向及纵向刚度折减系数分别为0.7 和0.01.在数值模拟中通常将盾尾空隙、注浆填充的程度、隧道壁面土体受扰动的程度概化为一均质、等厚、弹性圆环状等代层[20]，等代层厚度取30 mm.同样，将盾构机盾壳模拟为均质等厚的弹性圆环，根据盾构掘进过程中等代层在不同阶段的实际状态，将其分为：等代层1，此时模拟盾构机外壳；等代层2，同步注浆刚完成时的半液体状态；等代层3，注浆材料最终凝固，强度增加，注浆体材料的弹性模量取为同步注浆阶段的10 倍[19]，各阶段参数见表2.

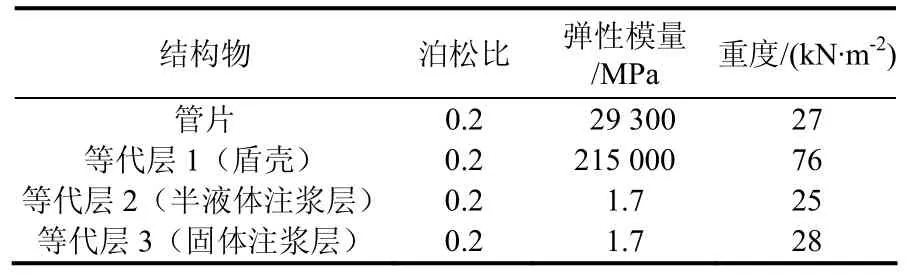
表2 结构物物理力学参数Tab.2 structural physical and mechanical parameters

2.4 盾构掘进过程模拟

初始位移清零→开挖面施加均布压力→开挖一个施工步长（取3 m 为一个施工步长[21]）→生成盾壳单元（等代层1）→开挖下一个施工步，将盾壳移除，生成管片单元，并将盾壳属性改为半液体注浆层属性（等代层2），并施加注浆压力→盾尾脱出后，注浆材料逐渐凝固，强度不断增加，此时，将半液体注浆层（等代层2）的属性转换为注浆体凝固后的属性（等代层3）.依次循环往复，直至盾构开挖完成.

3 曲线盾构施工土体位移影响

3.1 千斤顶不平衡推力比对土体位移的影响

盾构机在曲线段掘进时，通过千斤顶推力分区实现偏转，见图7.将掌子面沿中轴线分为左右两部分，分别设置不同的均布压力大小来模拟盾构机在曲线段因千斤顶不平衡推力对地层位移的影响，见表3.保持300 m 的曲线半径不变，分别设置4 组千斤顶不平衡推力.

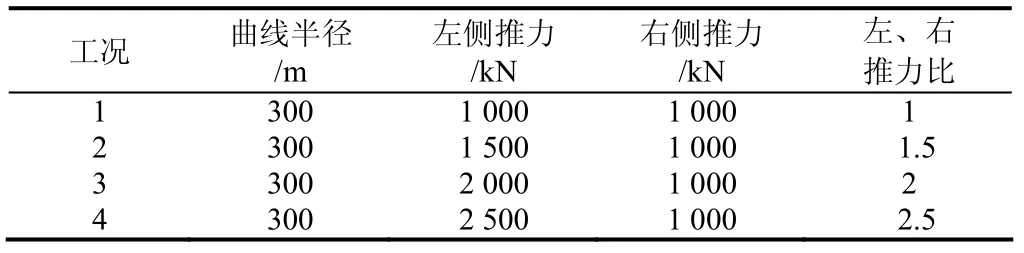
表3 不同工况下的计算参数Tab.3 calculation parameters under different working conditions

（1）不平衡推力比对地表沉降的影响

由图8 可知，数值模拟结果与实测地表沉降槽变形曲线基本吻合，且地表沉降槽呈现非对称性.地表沉降最大值位置向曲线内侧偏移.随千斤顶左、右侧推力比增加，地表沉降槽非对称性显著，且地表沉降最大偏移量与不平衡推力比呈正相关，工况1 至工况4 地表沉降槽偏移依次为3.25 m、4.02 m、5.22 m、5.88 m，其最大偏移约为最小偏移量的1.8 倍；验证了不平衡推力是引起地表沉降最大值向曲线内侧偏移的主要原因；随着左、右侧千斤顶推力比增加，盾构隧道施工对土层扰动的不均匀性增加，表现为地表沉降量呈增大趋势，模拟结果表明工况1 至工况4 地表沉降最大值依次为-28 mm、-31.72 mm、-33.58 mm、-38.61 mm，其最大沉降量比最小沉降量增加了38%.由此可见，小半径曲线盾构施工过程中应调整适当的千斤顶推力，以免因地表沉陷而造成工程事故.

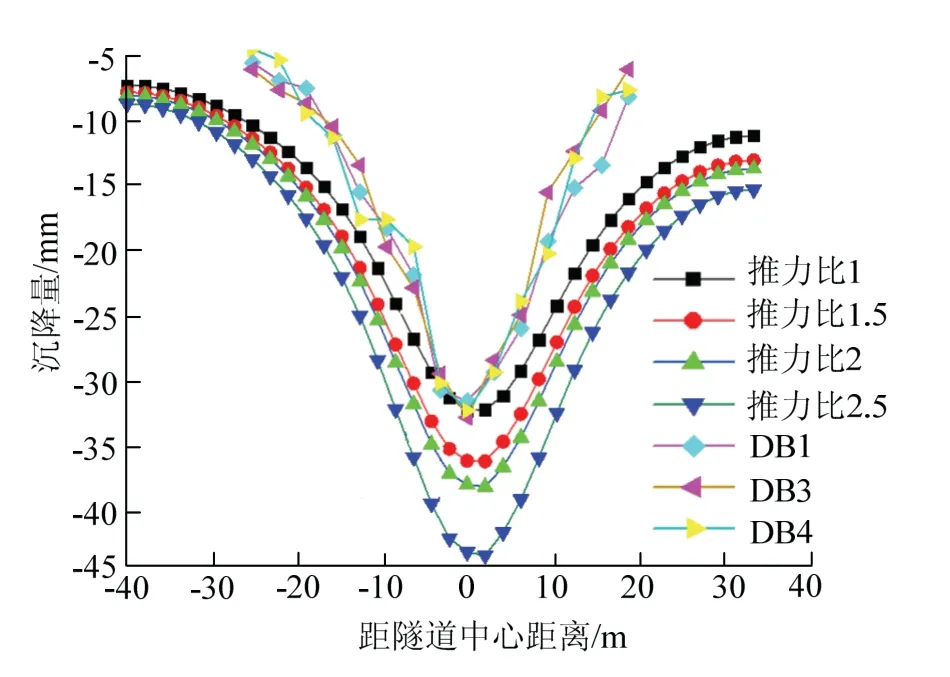
图8 不同千斤顶推力下的地表沉降Fig.8 surface subsidence under different jack thrust

（2）不平衡推力比对土体水平位移的影响

图9 为不同推力比时曲线内、外侧测斜的水平位移曲线，位置关系见图1.基于整体分析，盾构隧道曲线内、外侧测斜模拟值与实测值的变形趋势基本一致，但受现场实测过程中测量误差和盾构施工参数等因素影响，现场实测值与数值模拟具有一定的差异性.模拟结果表明：随着推力比增大，曲线外侧土体位于隧道顶部以上的土层受扰动程度越大，由于地层损失产生的沉降作用导致上方土体向隧道轴线方向位移，工况1 至工况4 的位移最大值依次为2.86 mm、3.07 mm、3.28 mm和3.49 mm；对于隧道范围的土层，受左侧推力增大的影响，土体向远离隧道方向移动，位移最大值依次为-4.66 mm、-4.91 mm、-5.17 mm和-5.41 mm.最大值比最小值增大约16.7%.

图9 不同推力时的水平位移Fig.9 horizontal displacement at different thrusts

随着左右侧推力比增大，对土体产生的不均匀扰动越大，曲线内侧土体朝向隧道方向位移增大，隧道所处的土层范围变化量最为明显，工况1至工况4 最大位移值依次为6.75 mm、7.10 mm、7.50 mm 和7.88 mm.最大位移值比最小值增大了约17%.因而小曲线盾构施工过程中应适当降低盾构外侧的顶推力或增加内侧顶推力，以减小盾构施工对曲线两侧土体的差异扰动.

3.2 曲线半径对地层位移的影响

为研究不同曲线半径对地层位移的影响，保持左、右侧推力为1 000 kN，分别对曲线半径为250 m、300 m、400 m、500 m 的4 种工况进行模拟，工况见表4.

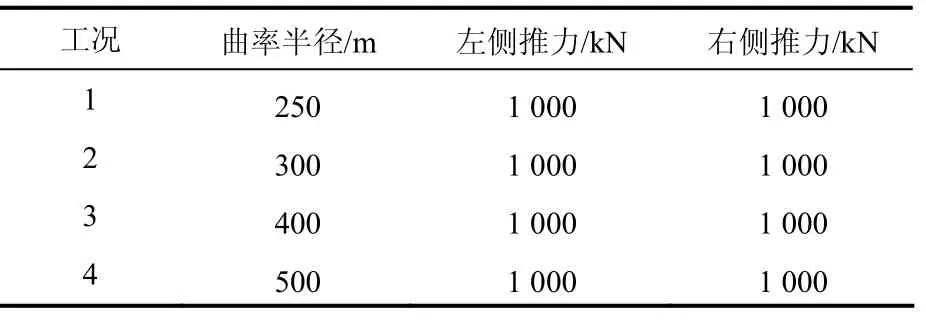
表4 不同工况下的计算参数Tab.4 calculation parameters under different working conditions

（1）曲线半径对地表沉降的影响

由图10 可知，地表沉降值与曲率半径的增大呈负相关，各工况对应的最大地表沉降值依次为-29.39 mm、-28 mm、-27.7 mm、-26.29 mm，工况1 比工况4 增大了约12%；同时，地表沉降最大值向曲线内侧的偏移随曲率半径的增大而减小，工况1 至工况4 的偏移依次为3.1 mm、2.89 mm、2.72 mm 和2.58 mm，最大偏移约为最小偏移的1.2倍.究其原因，随盾构曲率半径的增加，盾构施工转弯时需要超挖的土体量降低，对土体的扰动范围减小，因而地表沉降最大值及其偏移均随之减小.由此可见，小半径曲线盾构隧道施工过程中更应严格控制土体超挖量和不平衡推力，以降低隧道施工引起的地表沉降.

图10 不同曲率半径下的地表沉降Fig.10 surface subsidence under different radii of curvature

（2）曲线半径对深层土体水平位移的影响

见图11，数值模拟结果表明，随着曲率半径减小，盾构机蛇形摆动调整姿态，对周围土层造成剪切扰动，在盾构机周围产生更大的建筑空隙，曲线内外侧土体均表现出向隧道方向位移的趋势.曲线外侧位于隧道范围内的土层位移减小，隧道上方土层的位移值向隧道方向增大，工况1 至工况4 的最大位移依次为3.71 mm、3.49 mm、3.25 mm、3.02 mm，最大值约为最小值的1.23倍；曲线内侧土体因为曲率半径减小.刀盘对曲线内测土体超挖量增大，土体受扰动的范围增大，位移依次为 7.1 mm、6.75 mm、6.48 mm 和6.09 mm，最大值约为最小值的 1.17倍，因此，在小半径曲线盾构施工时，应做好轴线预偏，尽量减少因盾构机姿态偏转和刀盘超挖对土体的扰动.

图11 不同曲率半径下的水平位移Fig.11 horizontal displacement under different radius of curvature

4 结论

通过数值模拟与实测数据，研究郑州粉土地层小半径曲线盾构施工对周边土体位移的影响，得出以下结论：

（1）曲线盾构施工会引起地表沉降槽非对称变形，与直线盾构施工差异明显.保持盾构推力不变，在曲线半径500～250 m，地表沉降随曲率半径的减小而增大，最大地表沉降值增大约12%，沉降槽偏移也随之增大，最大偏移约为最小偏移的1.2 倍；保持300 m 曲线半径，在不平衡推力比1～2.5 内，沉降槽偏移和最大地表沉降值与推力比呈正相关，最大地表沉降值增大约38%，最大偏移约为最小偏移1.8 倍.

（2）不同于直线盾构隧道，曲线隧道左右两侧土体位移趋势有明显差别，曲线内侧土体位移朝向隧道方向，且变形主要集中在隧道范围的土层；曲线外侧隧道顶部以上土层位移朝向隧道方向，而隧道范围的土层背离隧道移动；从本文实测数据与模拟结果来看，即使距离盾构机仅0.9 m的土体其水平位移也很小，因此，在小半径曲线盾构施工中减小曲线内测土体的超挖量，调整适当的千斤顶推力，可有效减小其对周边土体及地下结构物的影响.

（3）通过现场实测验证本文数值模拟方法的可靠性，对于今后类似工程，可通过此方法为曲线盾构隧道的线型设计以及盾构施工时的推力设置提供参考，据此将盾构施工引起的周边土体地表沉降和水平位移控制在合理范围内.