城际旅客联程“行李直挂”服务最优定价
2021-09-11贾洪飞吴文静
贾洪飞,王 楠,吴文静
城际旅客联程“行李直挂”服务最优定价
贾洪飞,王 楠,吴文静
(吉林大学,交通学院,长春 130022)
针对联程联运的衍生产品“行李直挂”服务的最优定价问题,在对比分析携带行李的旅客采用直挂与非直挂模式下出行链差异性的基础上,考虑出行路径的客观条件和包括旅客不舒适性感受、换乘心理负担在内的心理因素,从在乘与换乘两个阶段量化直挂与非直挂模式下旅客的出行广义费用,并综合考虑运输商的利润与行李直挂所带来的价值链增值,提出服务价格的双层规划优化模型。上层以价值链最大为目标,下层为城市群多方式交通系统的平衡分配模型,最后通过算例对模型构建的合理性进行验证。结果表明:在铁路与航空的旅客运价分别为0.45元/(人·km)与0.75元/(人·km),两种方式下的行李直挂运价分别取0.003 8元/(kg·km)与0.006 2元/(kg·km)时可以达到价值链的最大化。研究结果为推进城市群旅客联程运输服务提供了理论依据和参考。
城际旅客;行李直挂;服务价格;双层规划模型
0 引 言
随着城市群区域经济一体化进程的加快,城际间旅客出行需求呈现快速增长且多样化趋势。城际间旅客出行的一大特征是多方式换乘且多携带行李。在不同方式间的换乘过程中旅客携带的行李需经历多次重复安检,这容易耽误乘客的行程计划,且携带行李上下台阶及步行大大降低了旅客出行的舒适性。伴随城际联程联运的不断发展,协调民航、铁路、公路等多方式密切合作,提供以枢纽为起讫点的“行李直挂”联运服务,不仅节省旅客出行时间且能满足旅客城际间出行的更高需求,而研究“行李直挂”对旅客出行的影响及直挂服务的合理定价是其实施的前提。
目前,“行李直挂”(Baggage Interline)联程服务国内仅限于航空,采用其他方式出行的旅客若不想随身携带行李,只能委托给快递公司邮寄行李,不仅需要支付较高的运费且运输时间长,如“次日达”服务。本文所设计的“行李直挂”服务是城市群联程联运服务的衍生产品,具有随到随取的特性,弥补了邮寄在时间上的缺陷,因此具有较好的市场前景。影响旅客对行李直挂服务选择的因素主要是以时间、价格等形式表征的出行成本。已有的对于旅客出行成本的研究包括了出行时间价值的度量[1]、出行链成本的构成[2]、多模式出行成本的测算[3]、乘客主观感知的换乘时间成本的测算[4-7]。在城市客运定价方法方面的研究,主要分为两类:(1)基于博弈理论的定价方法,如基于Hotelling模型的高速铁路与航空货运定价模型[8];基于鲁宾斯坦恩-斯塔尔议价模型的小件货物快运定价模型[9];基于两阶段博弈模型的高铁与航空运输的最优定价模型[10]。(2)基于双层规划模型的定价方法,如以运输价格、安全性、时效性和便捷性为广义费用的构成因素,构建多种运输方式竞争下的铁路或公路定价模型[11, 12];采用累积前景理论来描述乘客的有限理性,构建运输价格优化模型[13]。目前为止,对“行李直挂”模式与服务定价的探讨还不多见。
本文首先对携带行李的旅客在直挂与非直挂模式下感知的出行成本差异性进行分析;其次,从在乘与换乘两个阶段来量化两种模式下的出行广义成本;在此基础上,构建双层规划模型,包括以运输系统价值链最大化为目标的上层规划和寻求随机用户均衡的下层规划;最后,对模型进行求解并结合案例对行李直挂服务价格的合理性进行研究。
1 “行李直挂”模式分析
城际旅客一次出行全过程如图1所示。由于城际出行距离较长,在没有直达方式的情况下旅客需要采用两种及以上的交通方式出行。旅客在换乘站需要经历安检、排队等候、检票等环节及在不同方式站台间的走行。
“行李直挂”模式是将旅客与行李在整个联程过程中分离开来,形成独立的旅客链与行李链。对于在枢纽内走行、重复安检、检票的换乘旅客来说,“行李直挂”模式无疑极大地减轻了旅程的出行负担,行李异地交付服务提高了联程联运出行对旅客的吸引。
具体地,为组织“行李直挂”,运输企业还需关注的问题有:(1)行李运输过程的监控。方便行李托运工作人员与乘客查看行李安检与实时运送情况。(2)行李一次安检。由于航空、铁路、长途客运之间执行不同的安检等级标准,为方便乘客出行,安检系统仅执行乘客所购买的联程联运票中所涉及交通方式的最高安检等级标准来对托运行李进行安检,例如飞机—铁路联程,则采用飞机的安检标准进行行李安检。 (3)合理的行李直挂运费。依据行李的重量、体积、运输方式制定相应的收费标准,此外还包括行李丢失的赔付等工作。行李直挂给旅客带来了极大的方便,但是也对提供联运服务的运输企业提出了很大的挑战。在此,本文对行李直挂的服务定价问题进行研究。
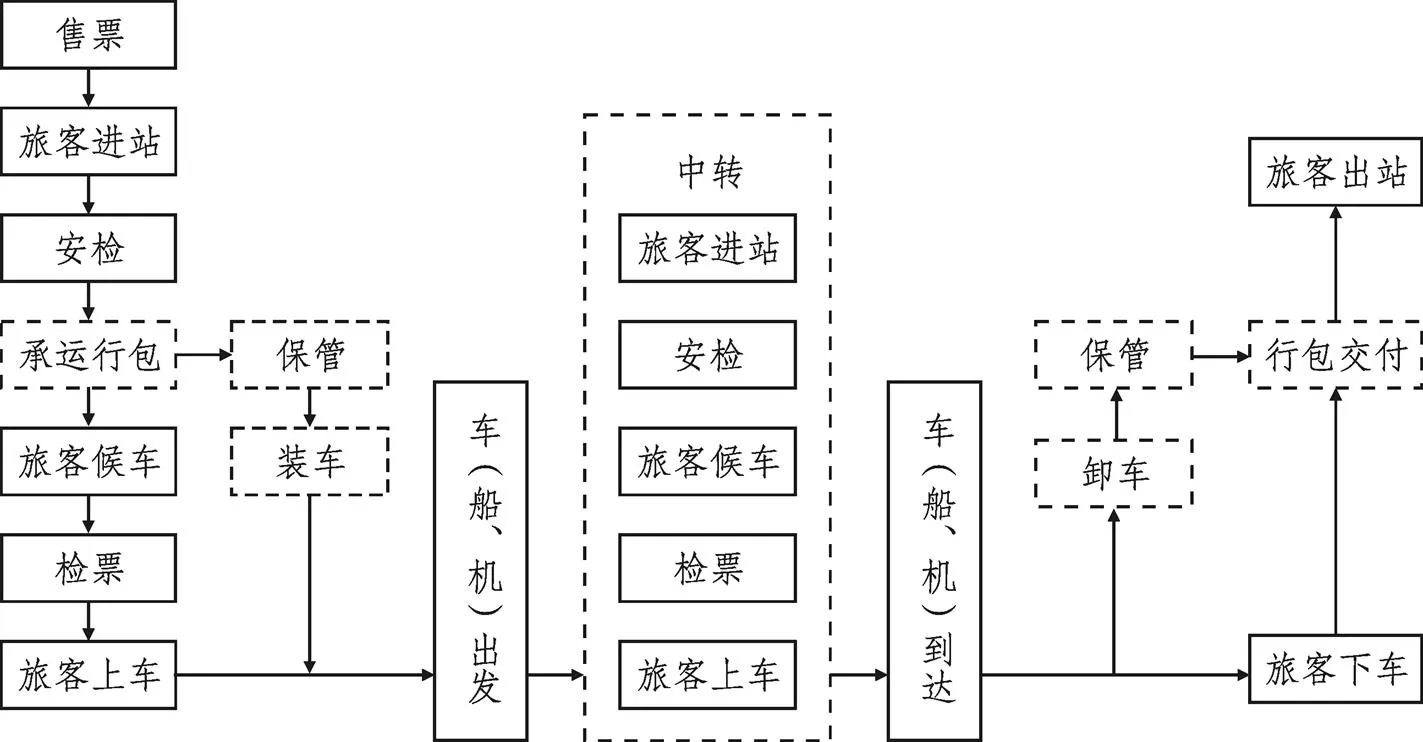
图1 城际出行的旅客出行链
2 出行广义费用
城际旅客一次出行全过程大多包含两个阶段:城市出行、城际出行。本文关注的是旅客以枢纽为起终点的城际出行,交通方式通常为航空、铁路、公路等。城际出行旅客的出行链可大致划分为两个过程:在乘段的在乘过程、换乘站的换乘过程。
2.1 在乘段广义费用
从旅客的角度出发,在乘段所支付的乘车费用多少、在乘时间长短、乘车舒适性与否是最直观的三大影响因素。本文参考文献[14],将乘车费用、在乘时间、不舒适性作为在乘段广义费用的构成。
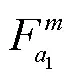
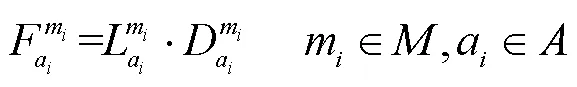
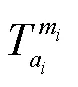
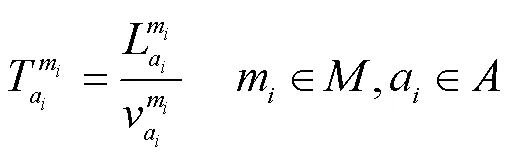

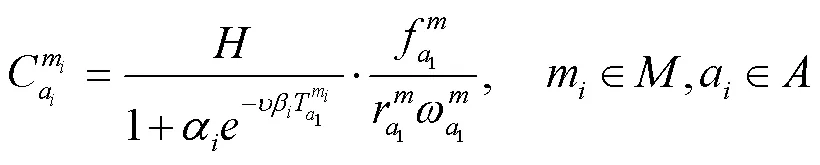
综合考虑乘车费用、在乘时间和不舒适性,得到携带行李旅客的在乘段广义费用,表达式为:
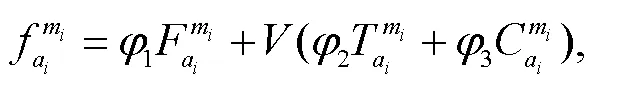
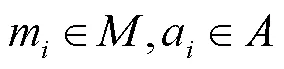
2.2 换乘广义费用
旅客在中转过程中需要经历枢纽站内不同站台间的走行、安检、候车、检票等过程,如果要经过多个枢纽站中转,旅客在换乘过程中的时间消耗将更大。携带行李的旅客不仅要承受换乘时间消耗,还将承担选择随身携带行李出行所可能带来的延误等风险,本文将其描述为换乘心理负担成本。因此,换乘广义费用由换乘时间与换乘心理负担所构成。
(1)换乘时间。旅客换乘走行将增加乘客的疲惫感,往往导致乘客换乘过程中所感知的时间比实际换乘时间要大,将旅客感知的换乘时间表示为实际换乘时间的指数形式。同时考虑换乘次数对出行的负效用,将换乘时间成本表示为:
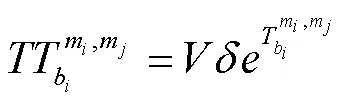
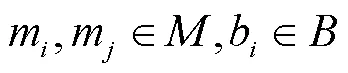
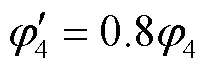
(2)换乘心理负担。换乘心理负担成本是乘客担心在换乘过程中,因延误等意外情况导致自己无法在规定的发车时间前到达候车处,耽误下一趟行程而产生的心理压力,这种心理压力在乘客换乘过程中较为明显。
假设换乘心理负担是与换乘时间相关的量,定义为其线性增函数,表达式为:
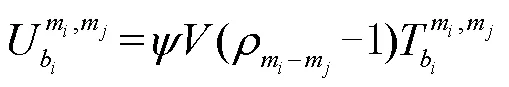
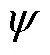
综合考虑换乘时间、换乘心理负担,得到携带行李旅客的换乘广义费用,表达式为:
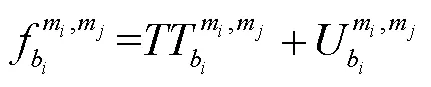
2.3 行李直挂服务费用
选择行李直挂服务的旅客,需在交通工具票价的基础上额外支付行李直挂的服务费用。目前,物流运费通常可以划分为三种计费方式:按重量、体积、重量或体积计费。其中快递的运费是根据产品类型及服务时效区分价格,采用“首重+续重”的计费模式。以顺丰为例,省外件一般起步价(1 kg以内)18元,续重为6~8元/0.5 kg。对于旅客行李的托运,飞机托运费是超过免费行李额的重量,按照每公斤经济舱票价的1.5%计算,国内航班托运行李免费额经济舱一般为20 kg。铁路的零担货物是区间定价,运价里程依据为《货物运价里程表》。
由此可见,在运费的计价方面,通常按照行李的重量与运输里程进行计费。在实际操作过程中,为了计费方便,多采用里程区间计费。为了简化计算,在此以实际里程为计费依据,同时参照航空的首重标准,以20 kg为行李直挂运输的免费重量,则直挂行李运费的计费方法为:直挂行李运费(元)=超额计费重量(kg)×计费里程(km)×行李直挂运价(元/kg·km)+其他费用(元)。
行李直挂服务费用的表达式为:
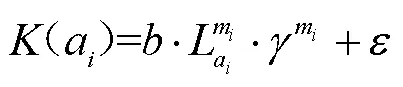
2.4 行李直挂时寄取行李排队时间成本
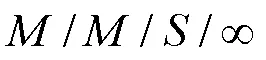
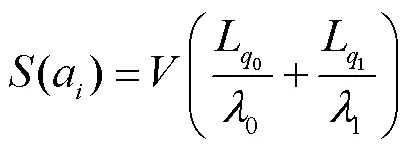
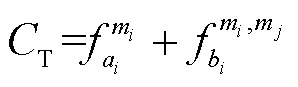
3 行李直挂价格最优模型
将双层规划方法应用于行李直挂服务定价问题中,其中上层决策者是运输管理部门,下层决策者为旅客。运输管理部门通过设置行李直挂服务来吸引旅客,而旅客则基于出行成本来选择行李直挂服务及相应的出行方式和路径。本文采用双层规划方法寻求直挂服务的最优定价,其上层目标是城市群客运系统的价值链最大化,下层目标是弹性需求下的多方式交通网络的随机用户均衡。
3.1 上层模型
价值链的分析适合于任何经济活动。通过对城市群旅客出行链分析可知(见图1),多方式换乘增加了旅客出行时间、体力消耗和心理负担,由换乘产生的负效应是影响旅客出行价值链的首要因素。而行李直挂服务可以实现对旅客换乘时间的节约及换乘心理负担的缓解,通过优化出行链环节实现旅客价值链的增值,但是行李直挂需要旅客额外的费用支出,包括服务等待与服务费。当价值链增值以出行广义费用盈余来衡量时,其增值可表达为:
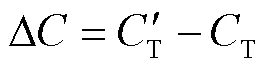
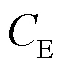
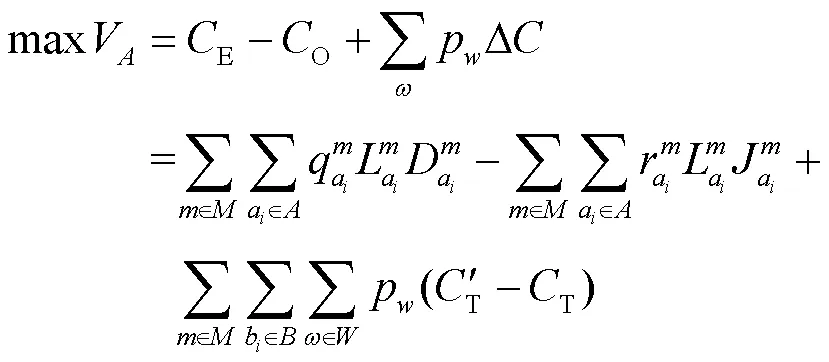
模型的约束条件包括枢纽能力约束、区间能力约束和客流关联约束等。
3.2 下层客流分配模型
由于“行李直挂”服务是在联程联运环境下执行的,因此旅客在购买联程票时,其出行方式及路径是相对确定的。旅客会考虑包括“行李直挂”服务价格在内的出行成本,依据效用理论选择直挂或非直挂模式及相应的出行路径。根据旅客的选择,最终各条路径的客流量达到平衡。在随机平衡分配模型中,平衡状态下OD对的交通量应满足以下条件:

针对下层模型中城市群客运网络中的用户均衡问题,采用相继平均法进行求解;针对上层模型,采用遗传算法进行目标函数的极值求解。
4 案例分析
4.1 基本假设
本文将所构建的模型运用到假设的城际客运网络中,如图2所示,该客运网络包含6个枢纽站,其中石家庄站、天津西站、张家口机场站都位于京津冀城市群。为了体现“行李直挂”运输在换乘中的优势,设计网络中的旅客出行距离较长,且都经过两次换乘。枢纽站1和6分别为旅客出行的起终点,在此假设为铁路站。在直挂模式下,旅客在1点进行行李的托运,在6点进行行李的提取。2、5为铁路换乘枢纽站,3、4为航空枢纽站,旅客在乘段的交通方式由该段起点的交通方式决定。
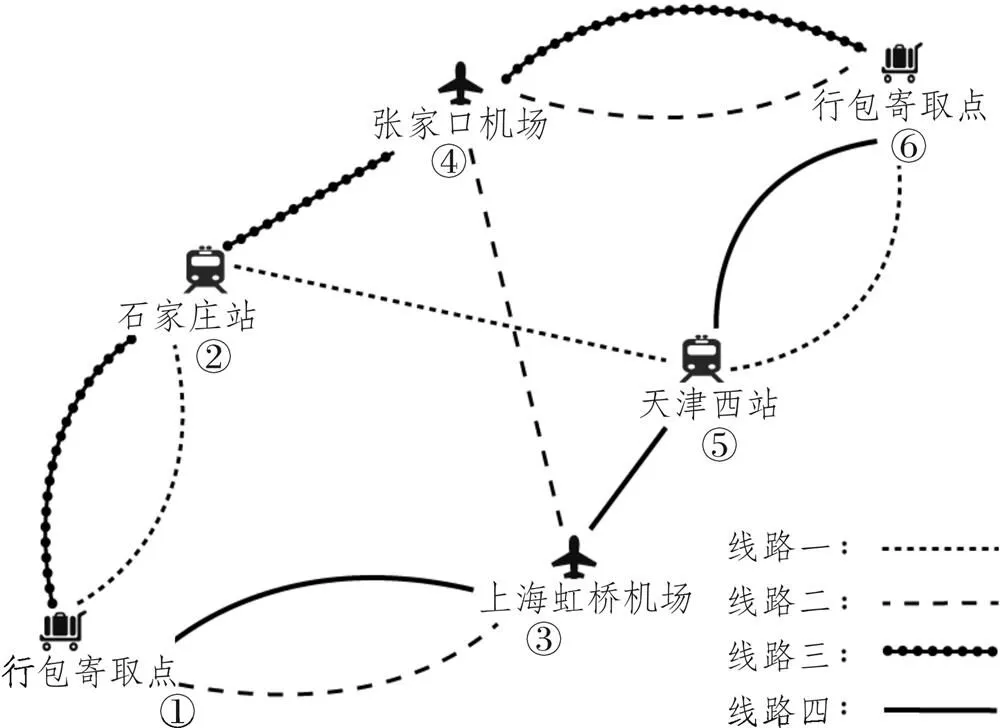
图2 算例网络示意图
由客运网络可知,旅客在起终点之间共有4条线路可供选择,分别为1—2—5—6、1—3—4—6、1—2—4—6、1—3—5—6。每一条线路旅客有两种选择:采取行李直挂服务或非行李直挂服务。
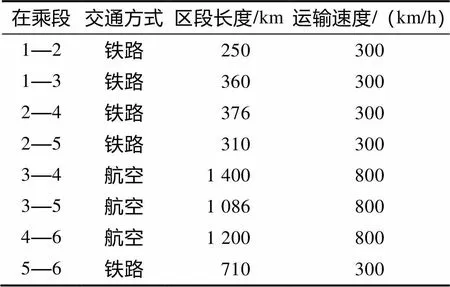
表1 运输网络基础数据
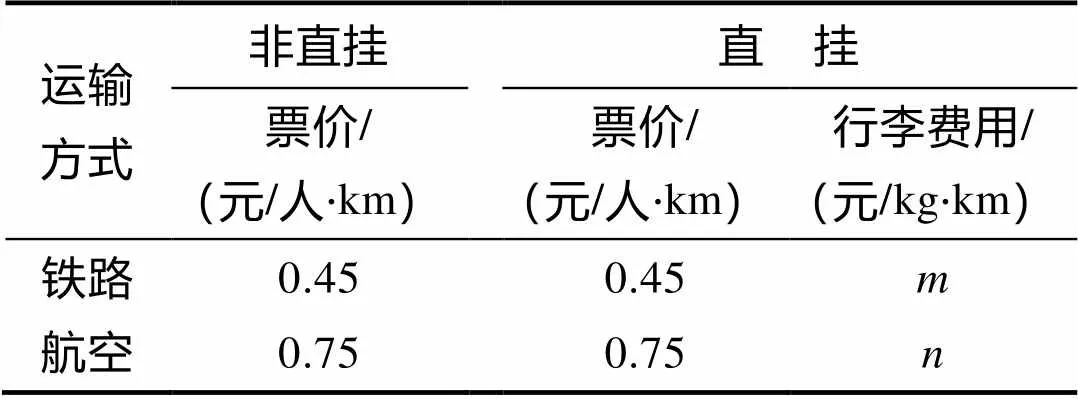
表2 单位运输费用
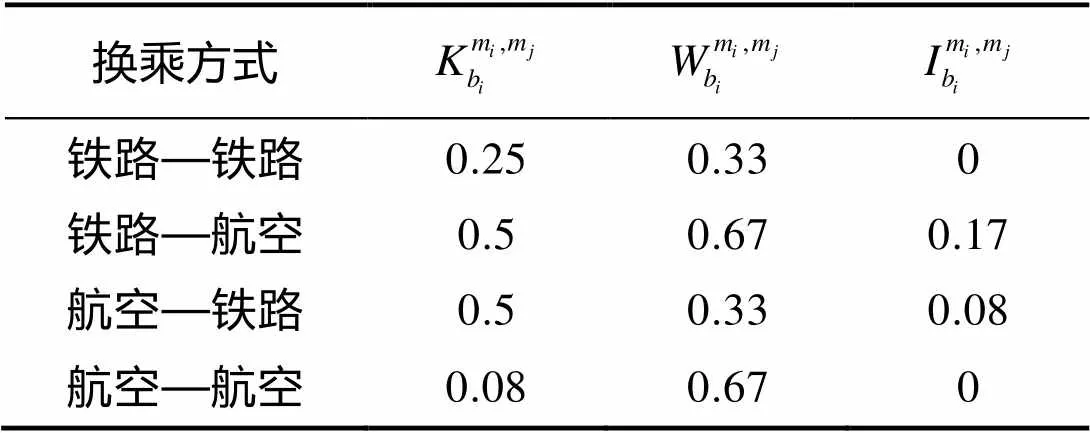
表3 参数取值 (单位:h)
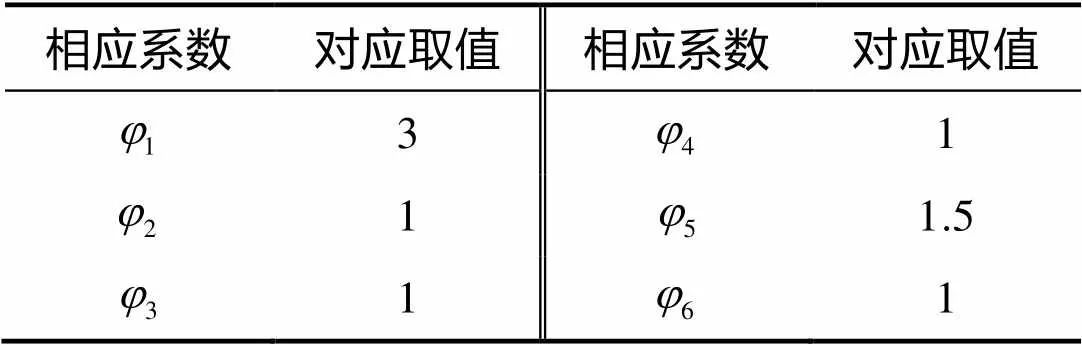
表4 系数取值
4.2 “行李直挂”服务的最优定价结果分析
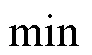
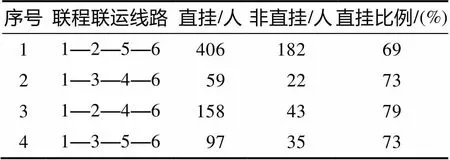
表5 客流分配情况

表6 行李直挂最优定价结果
以路径1—3—4—6为例,总长为2 160 km,其中铁路里程为560 km,航空里程为1 600 km。根据铁路与航空的运价,该路径的旅客票价为1 452元。假设旅客平均携带的行李为40 kg,行李直挂费用为241元,约占票价的16.6%。
以航空运输为例,对比航空行李托运费与行李直挂费用的差异。在航空运输中,超出免费行李额的部分统一计价标准按经济舱全价票的1.5%来收取。取3—4航空区段,即上海—张家口的航空运输为例,里程约为1 400 km,按照市场价格其全价机票约为1 300元,旅客携带40 kg的行李需要支付的额外托运行李费用为390元,本文计算获得的行李直挂运费为173.6元。由此可见,直挂费用比航空托运费便宜了216.4元,节省了50%以上。当然,这只是理论分析获得的价格差异,实际定价过程中还需要考虑到第三方行李运输服务商的成本与利益。
4.3 直挂与非直挂模式下旅客总出行时间与换乘时间对比
同样设起终点1—6的总客流量为1 000人,按等比例分配到四条路径,再将每条路径的客流平均分配至直挂与非直挂两种模式下,则每种模式每条路径分配人数为125人,对比不同模式下乘客的总出行时间与总换乘时间。结果显示,相比与非直挂模式,直挂模式下出行时间减少了975.0 h,换乘时间节约了850.05 h。以换乘时间为例,对比结果如图3所示,直挂模式下的换乘时间比非直挂模式下明显减少,线路1和2尤其明显。
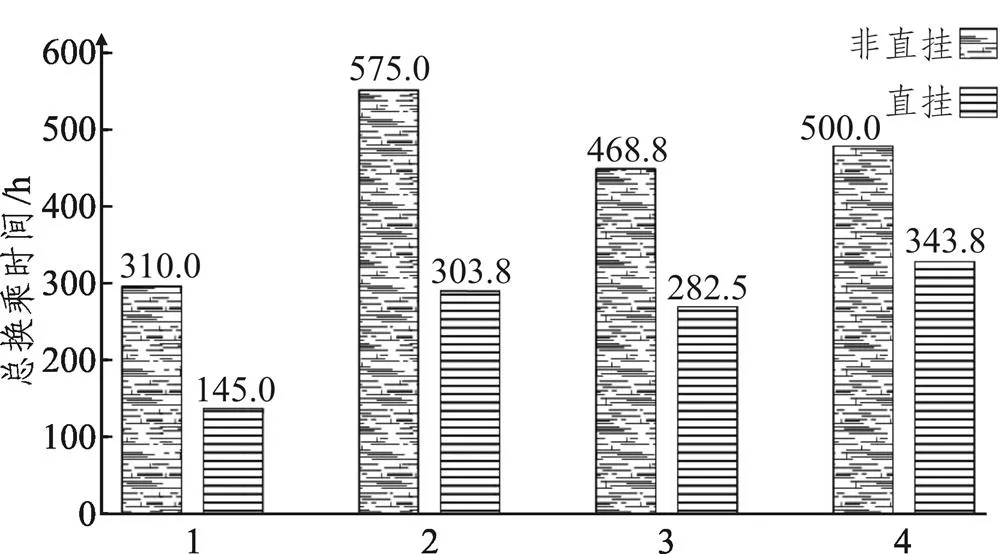
图3 直挂与非直挂模式下不同路径的总换乘时间对比
4.4 影响因素的敏感性分析
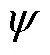
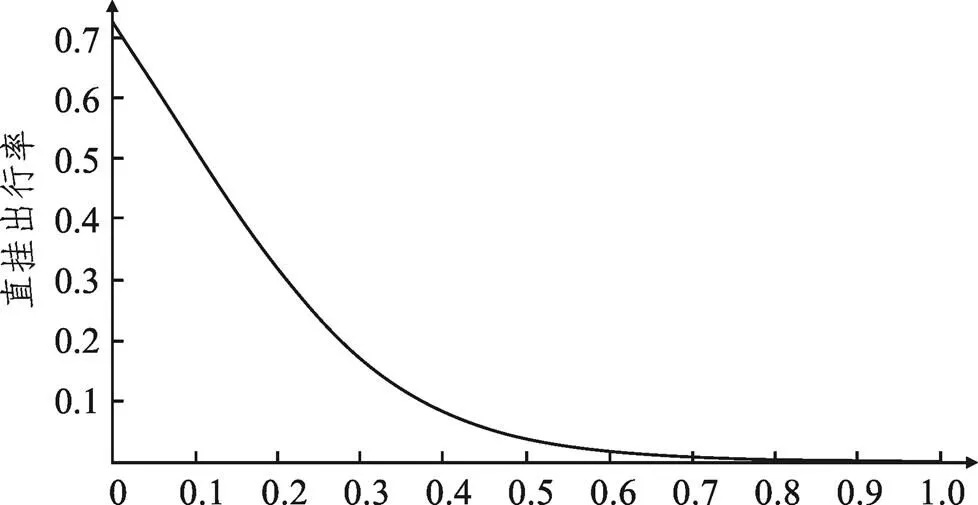
心理负担缓解系数ψ
5 结 论
以城际多方式旅客联程服务为背景,以价值链最大为目标,本文构建了“行李直挂”服务最优定价模型,并结合算例进行了模型的验证,主要研究结果如下:
(1)对比携带行李的旅客采取直挂与非直挂服务下旅客感知的舒适性、换乘时间、换乘心理负担的差异性,分别建立了两种模式下的出行广义费用函数。
(2)将价值链分析应用于旅客联程“行李直挂”服务,定义了直挂服务下的价值链增值函数,构建了以运输系统价值链最大化为目标的“行李直挂”价格最优的双层规划模型。
(3)通过算例求解,在铁路与航空的运价分别为0.45元/(人·km)与0.75元/(人·km),两种方式下的行李直挂费用分别取0.003 8元/(kg·km)与0.006 2元/(kg·km)时可以达到价值链的最大化。与上海—张家口旅客航空出行的行李托运费用相比较,行李直挂费用减少了50%以上。对比直挂与非直挂模式下出行者的总出行时间与换乘时间,直挂模式更优。
我国《国家新型城镇化规划(2014—2020)》的提出加快了城市群一体化进程,促进了城市群(如京津冀城市群)范围内旅客出行需求的快速增加。积极推进铁路、公路、民航等多种运输方式的客运联程系统建设,不仅能够缩短旅客出行时间,也能够节约运输成本。要提高联程联运对旅客的吸引,“行李直挂”服务的实现是非常重要的,本文提出的“行李直挂”服务的最优定价模型及方法为推动我国旅客联程联运的发展具有理论价值与借鉴意义。
除此之外,此模型与方法不仅适用于城际长距离的联程“行李直挂”服务定价,也适用于城市群范围内的联程服务定价。以京津冀城市群为例,旅客从首都机场至天津站,可选择在北京西站、北京站、北京南站换乘,换乘方式包括了机场大巴、地铁、出租车等市内交通方式。由此可见,考虑市内出行的城市群客运网络是比城际网络更为复杂的超网络,由于基础数据的缺乏,基于超网络模型中的相关参数目前无法估算。如果条件成熟,采用京津冀城市群实际数据对模型进行测算分析,将具有更加重要的现实意义。
[1] 田园. 城际铁路旅客出行时间价值研究[D]. 兰州: 兰州交通大学, 2018.
[2] 罗玉芳, 陈梦微, 王殿海. 出行方式链的转换成本估计[J]. 哈尔滨工业大学学报, 2020, 52(3): 11-17.
[3] ZHU J X, LUO Q Y, GUAN X Y, et al. A traffic assignment approach for multi-modal transportation networks considering capacity constraints and route correlations[J]. IEEE Access, 2020, 8: 158862-158874.
[4] WANG T, KE S. Transfer penalty of public transport[C] //International Conference on Education. Zhengzhou: ICESAME, 2017: 1711-1720.
[5] CASCAJO R, GARCIA-MARTINEZ A, MONZÓN A. Stated preference survey for estimating passenger transfer penalties: design and application to Madrid[J]. European Transport Research Review, 2017, 9(42): 1-11.
[6] SI B F, ZHONG M, LIU J F, et al. Development of a transfer-cost-based logit assignment model for the Beijing rail transit network using automated fare collection data[J]. Journal of Advanced Transportation, 2013, 47(3): 297-318.
[7] JIN F L, YAO E J, ZHANG Y S, et al. Metro passengers’ route choice model and its application considering perceived transfer threshold[J]. Plos One, 2017, 12(9): 1-17.
[8] 王焯, 蹇明. 基于博弈论的高速铁路与航空货运定价影响研究[J]. 铁道科学与工程学报, 2019, 16(10): 2414-2420.
[9] 孙熙安, 成瑞利. 公路客运小件货物快运包仓定价研究[J]. 交通运输系统工程与信息, 2017, 17(4): 13-18.
[10] TSUNODA Y. Transportation policy for high-speed rail competing with airlines[J]. Transportation Research Part A: Policy & Practice, 2018, 116: 350-360.
[11] 周焱, 李鹏飞, 朱绪斐, 等. 竞争条件下高速铁路定价方法研究[J]. 交通运输工程与信息学报, 2016, 14(1): 101-106.
[12] 张志博, 刘杰鑫, 杨雨, 等. 基于公路货物运输价格的竞争性铁路货物运输浮动定价方法研究[J]. 交通运输工程与信息学报, 2018, 60(2): 100-104.
[13] LI X Y, LI J. A freight transport price optimization model with multi bounded-rational customers[J]. Transportation, 2019, 48(1): 477-504.
[14] 汪勤政, 四兵锋. 换乘约束下城市多方式交通分配模型与算法[J]. 交通运输系统工程与信息, 2017, 17(4): 159-166.
[15] 刘秉政, 葛颖恩, 曹凯. 考虑乘客主观评判的地铁与公交的票价及换乘优惠率优化[J]. 系统工程理论与实践, 2016, 36(12): 3188-3197.
[16] 韦凌翔, 陈红, 蒋金亮, 等. 基于广义费用函数的高铁票价双层规划模型研究[J]. 铁道科学与工程学报, 2015, 12(2): 250-256.
Optimal Pricing of Intermodal “Baggage Interline” Service for Intercity Passengers
JIA Hong-fei, WANG Nan, WU Wen-jing
(Transportation College, Jilin University, Changchun 130022, China)
This study determines the optimal pricing for “Baggage Interline” service, which is a derivative product of urban agglomeration intermodal transport service. The differences of travel chain between the modes of Baggage and Non-Baggage Interline are compared and analyzed. Stages of in-ride and transfer considering the objective conditions of travel paths and the psychological factors, which includes passengers’ uncomfortable feelings and transfer psychological burden, are used to construct the generalized travel cost of passengers between the modes. Comprehensively considering the profit of the transporters and the value-added of the value chain brought by the “Baggage Interline” service, a bi-level programming model with the optimal service price is proposed. The upper level maximizes the value chain, and the lower level is the balanced allocation model of the multi-mode transportation system of the urban agglomeration. Finally, the rationality of the model is verified using an example. The results indicate that when the railway and airline rates are 0.45 and 0. 75 yuan/(passenger·km), the value chain can be maximized when the service charge of “Baggage Interline” service is 0.003 8 and 0.006 2 yuan /(kg·km) separately. This provides a theoretical basis for promoting the development of passenger intermodal transport in urban agglomeration.
intercity passenger; Baggage Interline; service charge; bi-level programming model
1672-4747(2021)03-0022-09
U125; F505
A
10.19961/j.cnki.1672-4747.2021.03.008
2021-03-08
2021-04-20
:2021-04-29
2021-03-08~03-09;03-16~03-24;04-16;4-20
国家重点研发计划项目(2018YFB1601300)
贾洪飞(1969—),男,山东青岛人,教授,研究方向为综合运输系统规划,E-mail:jiahf@jlu.edu.cn
吴文静(1980—),女,江苏苏州人,教授,研究方向为运输系统规划,E-mail:wuwj@jlu.edu.cn
贾洪飞,王楠,吴文静. 城际旅客联程“行李直挂”服务最优定价[J]. 交通运输工程与信息学报,2021, 19(3): 22-30.
JIA Hong-fei, WANG Nan, WU Wen-jing. Optimal Pricing of Intermodal “Baggage Interline” Service for Intercity Passengers [J]. Journal of Transportation Engineering and Information, 2021, 19(3): 22-30.
(责任编辑:李愈)
