不确定需求下铁路集装箱动态定价研究
2021-09-11唐慧敏张小强
唐慧敏,谭 雪,张小强,梁 越
不确定需求下铁路集装箱动态定价研究
唐慧敏1,谭 雪1,张小强1,梁 越2
(1. 西南交通大学,交通运输与物流学院,成都 611756;2. 交通与城市规划设计研究院,中铁二院工程集团有限责任公司,成都 610031)
针对铁路集装箱运输需求的不确定性,本文将传统线性需求模型、多元logit需求模型与基于LSTM神经网络的深度学习需求模型进行对比,以铁路承运企业利润最大为目标函数建立集装箱动态定价模型。首先,提取与集装箱运输需求相关的特征向量,采用梯度下降算法标定线性模型、多元logit模型参数和监督式学习方法训练LSTM神经网络。需求模型实验显示,与线性、多元logit模型相比,LSTM深度学习模型对集装箱运输需求的拟合精度更高。在此基础上,设计精英选择策略遗传算法结合LSTM网络的动态定价反馈机制求解集装箱动态定价模型。实例结果表明,基于LSTM网络的铁路集装箱动态定价模型能有效提升铁路货运企业收益。
铁路运输;动态定价;需求模型;收益管理;长短期记忆网络;
0 引 言
2019年我国铁路集装箱发送量同比增长30%,但运输收入增幅仅为13%[1],铁路集装箱运输在现有需求下有较大盈利空间。我国铁路货运价格长期以来一直遵循政府定价制度,公路运价则相对灵活,因此公路运输在激烈的市场竞争下拥有更强的盈利能力。为推动铁路市场化改革,我国发布的《关于调整铁路货运价格进一步完善价格形成机制的通知》中指出应适当调整铁路货运价格,并建立运价上下浮动机制。当前已开放包括集装箱运输在内的四项铁路运输价格,自此铁路承运企业拥有更大的运输自主定价权力。在此情况下,制定动态科学的集装箱运输价格是铁路公司抢占货运市场、提高运营收入的必然选择。
动态定价是短期运营中管理需求、提升利润最为有效的手段,其核心是以需求为导向在各类约束条件下制定最优价格策略[2]。需求模型是价格策略优化的必要前提,只有对需求进行准确的刻画,才能制定有效的定价策略提升企业收益。部分研究直接假定需求满足某类概率分布,例如:需求满足泊松分布[3]、Beta分布[4]等,得到确定需求下的定价策略,此类型需求不考虑外在因素对需求的影响。大部分动态定价研究则是根据价格和需求相关因素的历史数据,建立需求函数/价格响应函数。由于各因素之间相互作用关系事先是不确定的,因此一般先假设因素之间满足线性或非线性的相互作用关系,确定需求形式后再求解模型参数。目前常见的需求模型有线性模型[5]、指数模型[6]、logit模型[7]。针对与铁路集装箱需求类似的时间序列,目前也有相关分析方式,例如:VAR[8]、ARIMA[9]等,但这类方法对数据平稳性要求严格,且无法获得因素对序列的影响及规律[10]。
铁路运输网络复杂,货物运输需求不仅受政策、经济以及竞争的影响,还呈现地域性、趋势性、季节性等复杂特征。上述传统需求模型,提前对需求模型进行假设,然后再进行参数拟合。由于参数有限,难以全面描述运价与集装箱量的变动关系及各因素间的耦合关系,据此需求模型制定的最优定价可能并非最优。深度学习方法以其强大的数据处理能力和学习能力,不假设任何数据间关系,已被广泛用于挖掘各类数据之间的潜在联系。目前已运用到电力需求与价格关系研究[11]等领域,能通过实际数据集监督训练直接实现综合因素影响下的需求与电价之间的结构化输出。其中长短期记忆网络(Long Short-term Memory, LSTM)作为一种特殊的循环神经网络(Recurrent Neural Network,RNN),是一种能处理时间序列的深度学习神经网络,对序列的非线性特征进行学习具有一定的优势。与基础RNN相比,LSTM能避免因时间序列上节点距离较远而产生的梯度爆炸和梯度消失的问题[12],适合用于铁路这种决策周期较长的行业。
本文建立铁路集装箱动态定价模型,选择目前使用最广泛的线性、logit模型及基于LSTM网络的深度学习模型对铁路集装箱市场需求进行拟合,并设计遗传算法求解最优定价。
1 铁路集装箱动态定价模型
本模型着眼于铁路运输网络中的集装箱运输班列,对OD间的集装箱运输销售价格做出决策。基于收益管理的思想,以铁路承运企业集装箱利润最大化为目标函数,以运力限制和政府制定的价格限制为约束条件,建立铁路集装箱动态定价模型。
1.1 符号说明
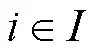
1.2 模型构建
铁路承运企业的运输收入:
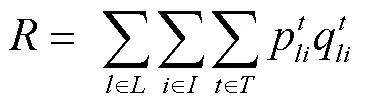
集装箱运输成本:
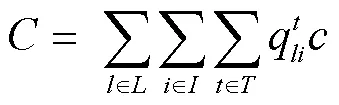
模型的目标函数为利润最大:
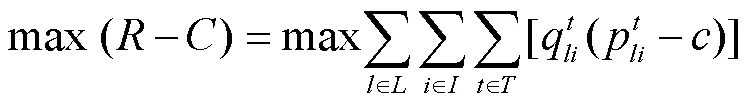
1.3 约束条件
各站点的实际发送量不超过各站点的集装箱发送能力:
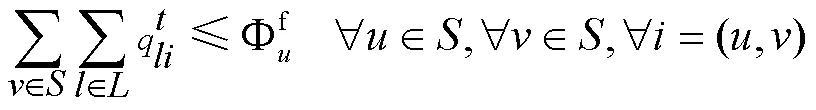
各站点的实际到货量不超过各站点的集装箱到达作业能力:
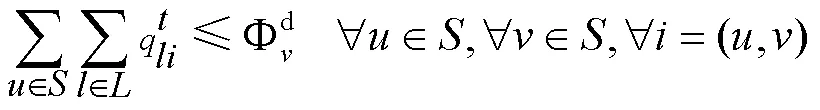
运价调整的上下限约束:
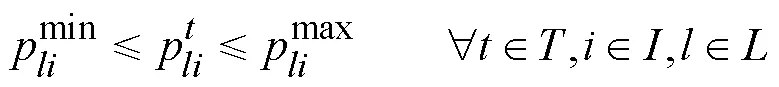
集装箱实际运输量不大于集装箱需求量:
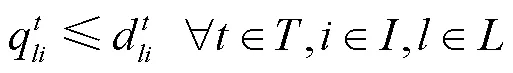
集装箱运输需求随运输定价的变动情况:

2 传统需求模型与深度学习网络需求模型
铁路货运系统具有动态性和不确定性[14],在实际的铁路运输市场中需求与价格以及其他因素的影响关系也是不确定的。目前的研究大多假设价格和其他因素同需求呈线性或非线性关系,因此对需求模型的刻画有多种参数形式。本节选择典型线性、多元logit模型这类传统需求模型以及基于LSTM网络深度学习模型进行对比研究。
2.1 需求模型的影响因素
2.1.1 传统需求模型的影响因素
2.1.2 深度学习网络需求模型的影响因素
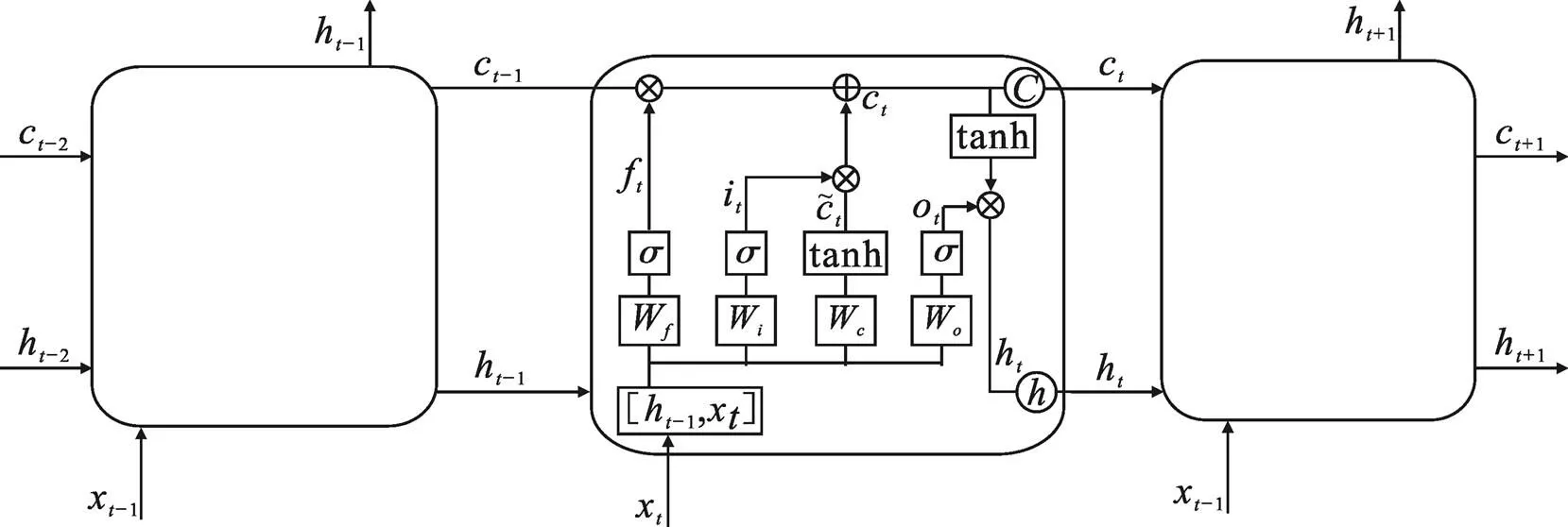
图1 LSTM网络及细胞结构
2.2 三种需求模型
2.2.1 线性模型
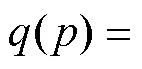
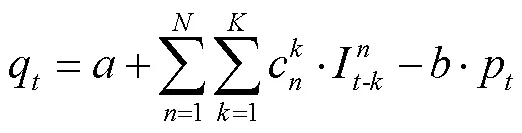
2.2.2 多元logit模型
目前应用较广的需求模型是logit模型,该模型的优势在于它可以清晰地模拟需求分配过程,本节的研究问题为决策周期内明确估计出客户在铁路运输和公路运输中选择铁路运输的概率。根据多元logit模型的定义[12]可知:
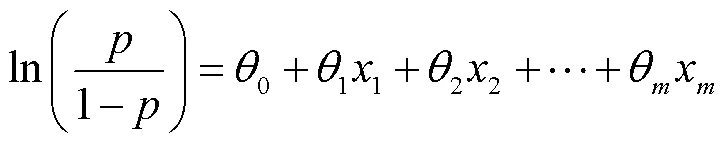
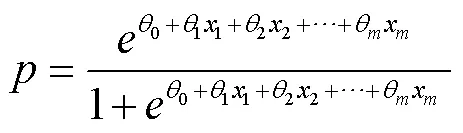
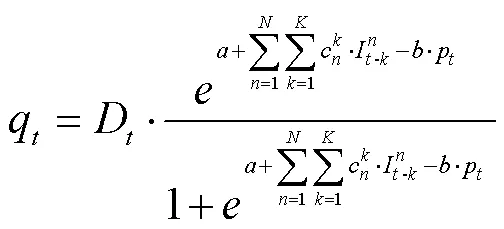
2.2.3 LSTM神经网络模型
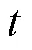
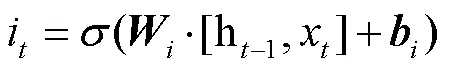
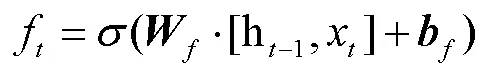
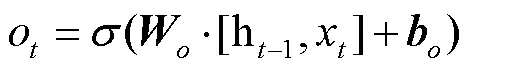
④ 隐藏向量的更新方式:
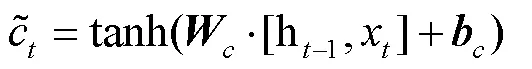
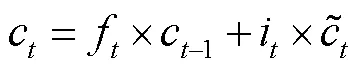


3 基于精英选择策略的遗传算法与LSTM反馈机制
当需求模型是线性或者logit形式时仍可采用求解线性/非线性规划的经典数学规划方法。基于LSTM网络构建的模型无法给出具体表达式,无法使用常规求解方法。对此可采用遗传算法(Genetic Algorithm, GA)搜索最优解。本文将铁路集装箱动态定价模型的目标函数定为适应度函数,直接使用训练后的LSTM网络输出端与遗传算法相结合,形成反馈机制。
为简化编码过程,本文直接采用实数编码方式,无须编码解码以便GA生成的初始种群可直接接入LSTM网络输入端口,LSTM网络输出的运量结果直接接入GA中计算个体适应度。但传统GA在使用实数编码时更易陷入迂回,导致运行速度不高也易陷入局部最优解。因此本文采用基于精英选择策略的遗传算法(elitist model based on GA,e-GA)求解,结合LSTM网络后,算法结构如图2所示。
具体步骤如下:
Step 3 计算初始种群对应的铁路货运需求。将初始种群数据输入训练后的LTSM网络,求得需求数据。
Step 4 计算个体适应度函数值。使用ranking函数以铁路集装箱动态定价模型目标函数的负数来计算个体适应度,遵循目标函数的值越大适应度值越高。约束条件使用罚函数直接找到非可行解个体,修改其目标函数值为0。
Step 5 判断适应度值是否稳定。比较前后两次输出的适应度误差是否小于预设误差容限。若小于误差容限则输出结果,否则转至下一步。
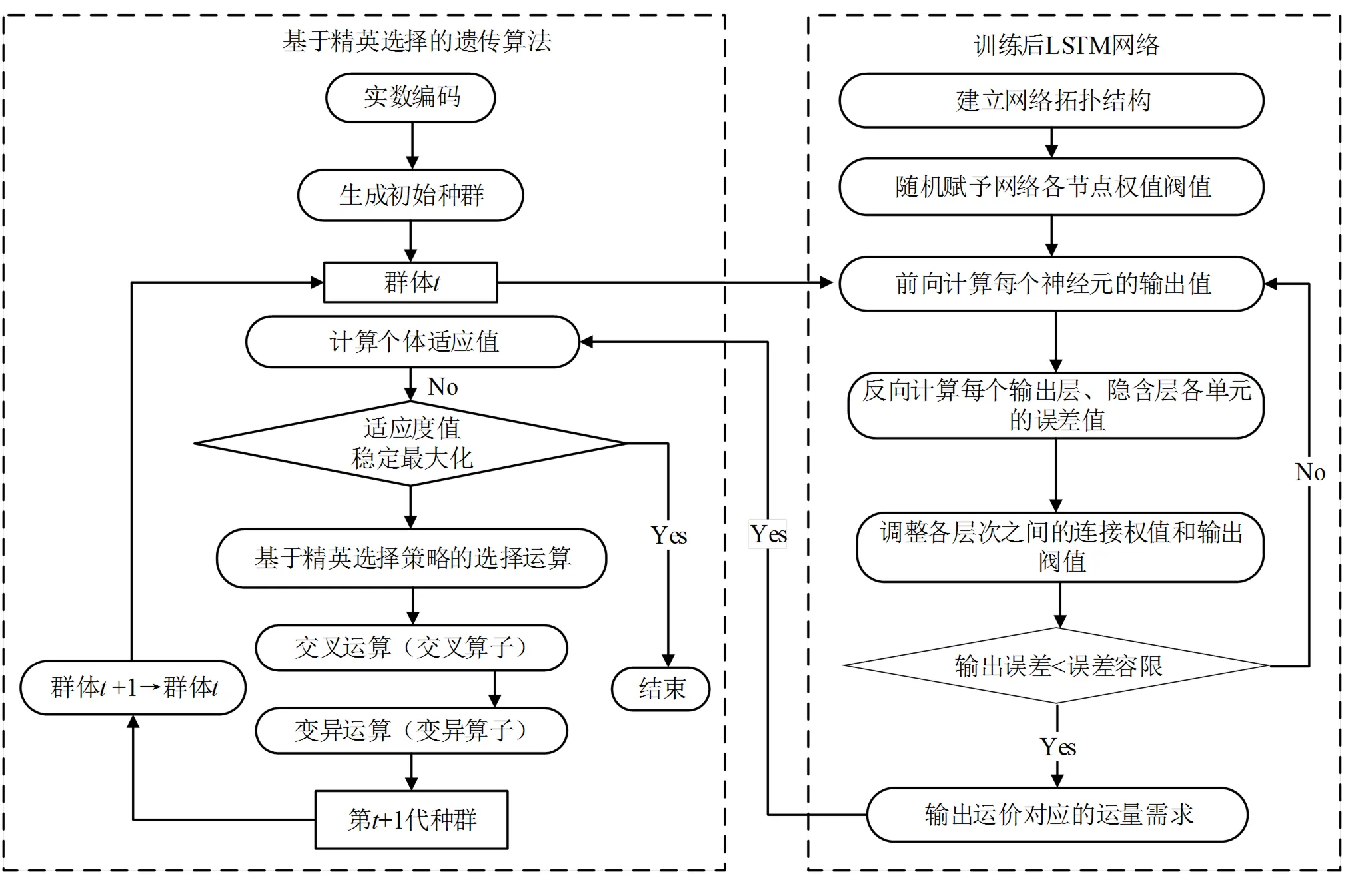
图2 算法流程图
Step 6 选择算子。精英复制选择,将当前适应值大于下一代最佳个体适应值的精英个体,建立精英个体的索引直接复制到下一代。
Step 7 交叉算子和变异算子。本文采用多点交叉,随机生成多个交叉点,并在交叉点进行交换。变异算子选择染色体片段逆转变异算子,与交叉算子一起完成种群的进化。
4 实例分析
4.1 铁路集装箱需求模型
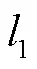
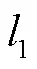
由图3(a)可知,铁路集装箱量以年为单位呈周期性变化,有明显的季节性特征,2015年后总体运量骤减。运价总体变动平缓,2017年前无法判断运价与运量之间的弹性。图3(b)表明2017年运价调整对应运量变化,说明铁路运输市场客户对运输价格敏感。同时根据整体走势可知,铁路集装箱运量变化趋势复杂,无法直接判断其实际符合的需求模型,因此在本节将使用上文构建的线性、多元logit模型以及LSTM网络需求模型对数据进行拟合。
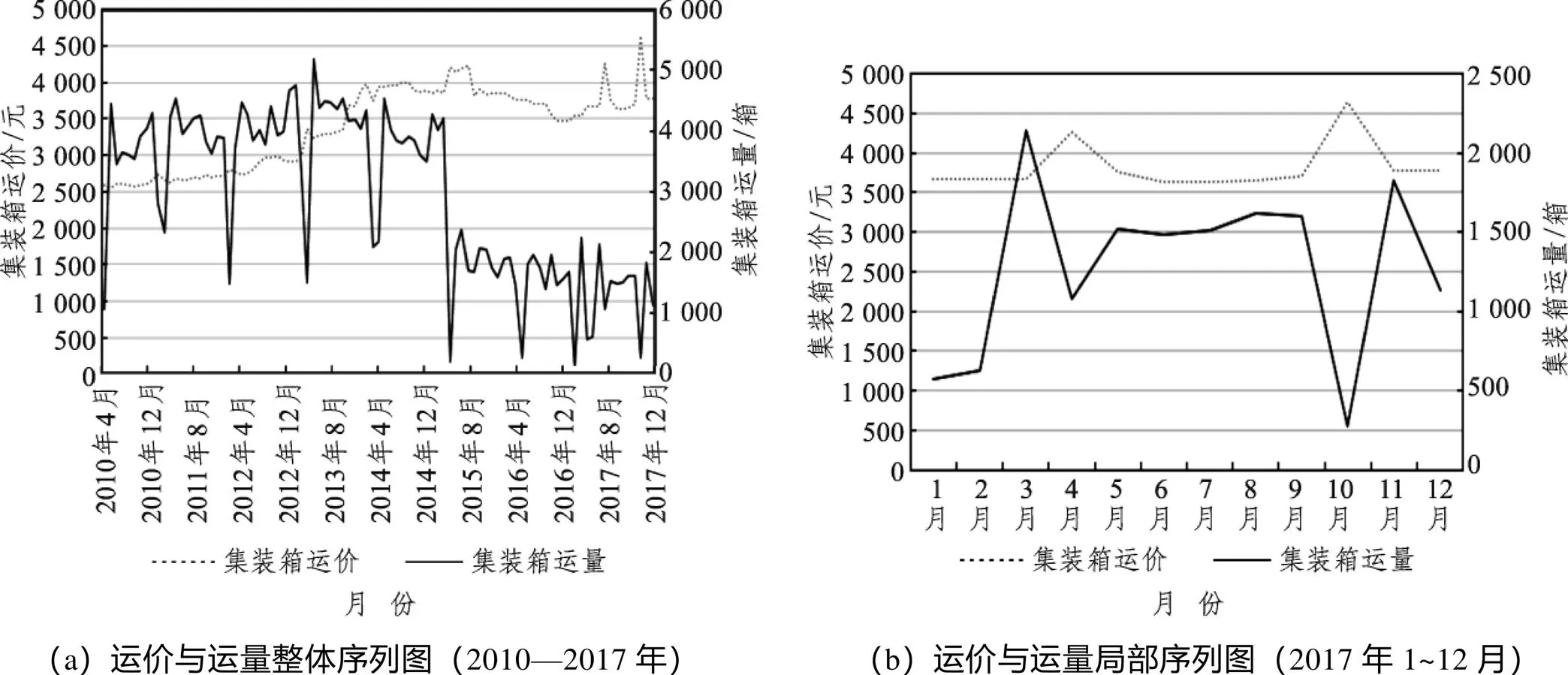
图3 运量与运价序列图
4.1.1 特征分析
为验证输入指标的有效性,本节对所选取指标的有效性进行评估和筛选。因为其中经济指标包括广东省GDP、四川省GDP、广东第一产业产值、广东第二产业增加值;竞争指标包括广东省公路集装箱量、道路集装箱运价指数,以及该路局铁路集装箱运输价格和铁路集装箱运量。对上述指标与铁路集装箱运量做相关性分析,得相关系数如图4所示。
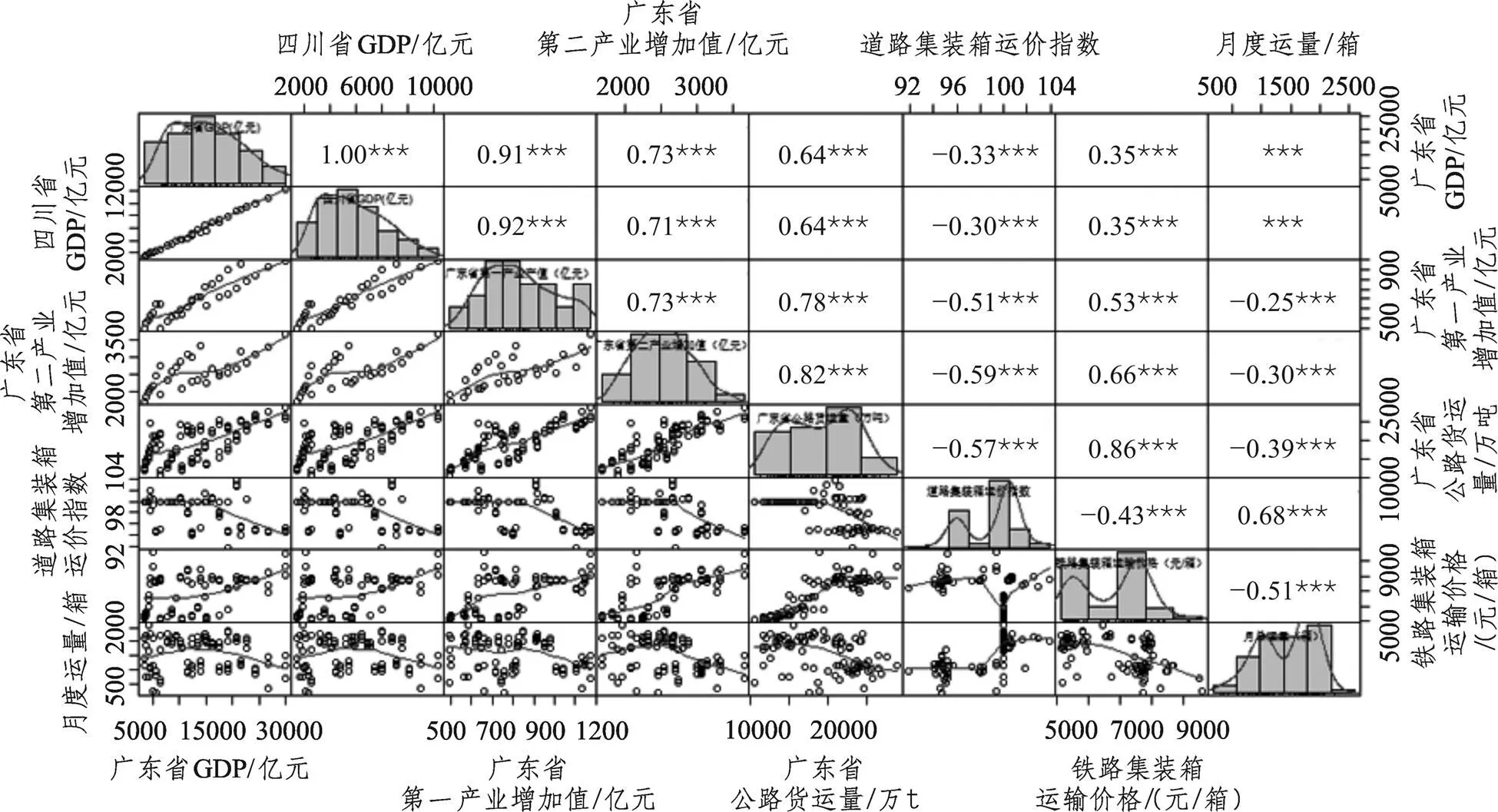
图4 相关系数图
数值代表相关系数,星号代表显著程度。由图4可知,两省份GDP与集装箱量的相关性不显著,可能是由于GDP数据为季度数据而非月度数据,无法体现GDP在月度间的变化情况。因此确定输入特征为:宏观经济指标(广东省第一产业产值、广东省第二产业增加值)、竞争因素指标(广东省—四川省公路集装箱量、公路集装箱价格指数、铁路集装箱运价、铁路集装箱运量)。
4.1.2 数据处理
为消除数据量纲对结果的影响,对原数据进行预处理。数据预处理包括数据归一化、划分训练集测试集和时间序列构建。训练前将数据如式(19)进行归一化处理,分为训练集(2010—2016年)和测试集(2017年),并构建时间序列:

4.1.3 训练方法
线性与多元logit模型是典型的参数模型,大多采用直接令原函数对该参数的偏导值为0的方式得到该参数的解析解,但易出现过拟合的问题,需要添加正则项等方式进行优化。
因此本文采用梯度下降法,结合Early Stopping方法求解线性及多logit模型的参数矩阵。当前后两次迭代时损失函数的差值降至最小时,输出当前对应的参数值。LSTM神经网络通过Early Stopping方法和Adam算法确定参数取值。选择均方误差MSE(Mean Square Error)作为损失函数对各模型进行训练:
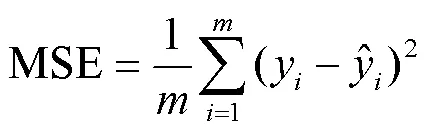
4.1.4 评估指标
考虑评价标准在实际情况中的现实意义,本文选择均方根误差RMSE(Root Mean Square Error)作为模型的评价指标:
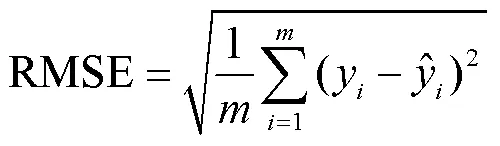
4.1.5 实验结果
本文LSTM神经网络的超参数取值:一层LSTM循环层、两层全连接隐藏层、一层dropout层和一层dense层,具体参数为5个神经元、10个神经元、随机丢失概率(0.1)和1个神经元,激活函数采用relu函数。将线性、多元logit模型和LSTM网络在测试集中的表现结果进行比较,并分析价格与需求之间的动态关系,测试集上评价指标结果如表1所示。
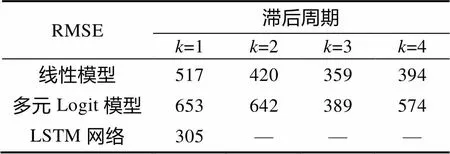
表1 结果评价指标
选择线性函数(= 3)、多元logit模型(= 3)以及LSTM神经网络需求模型在2017年测试集的真实值与计算值进行测试,绘图如图5所示。
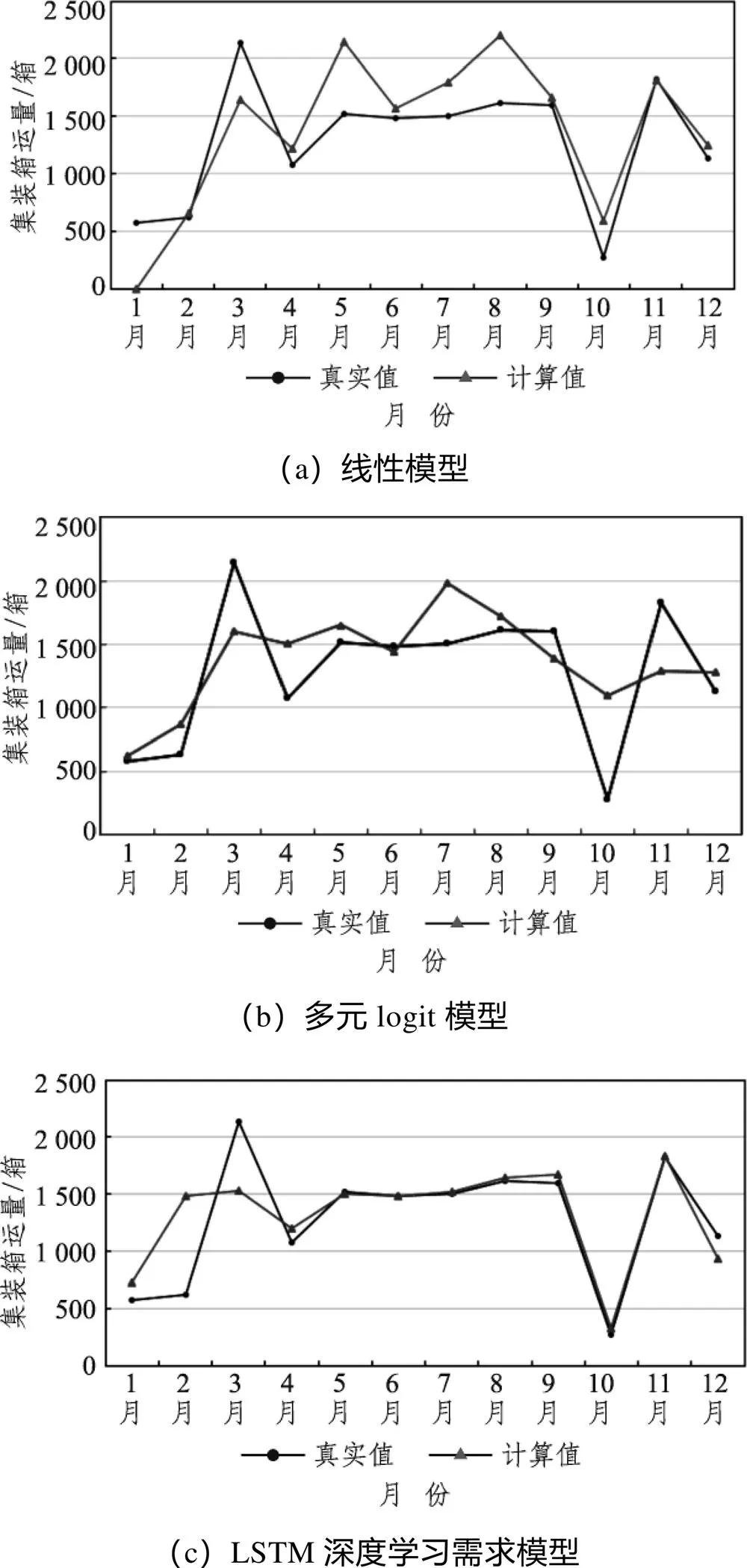
图5 测试集集装箱量中真实值及计算值对比
综上,训练后的LSTM神经网络需求模型对铁路集装箱市场的拟合程度最好。由于LSTM需求模型是非参数化模型,无法直接分析其各因素间的耦合关系。因此通过控制价格不变,其他因素参照实际情况输入,分析集装箱运量在运价不变时的波动情况。保持2017年月度其他影响因素值不变,在价格区间[2 400, 5 000]元内变动铁路集装箱运输价格,训练后的LSTM神经网络输出对应集装箱需求,选择部分月份制图如图6所示。
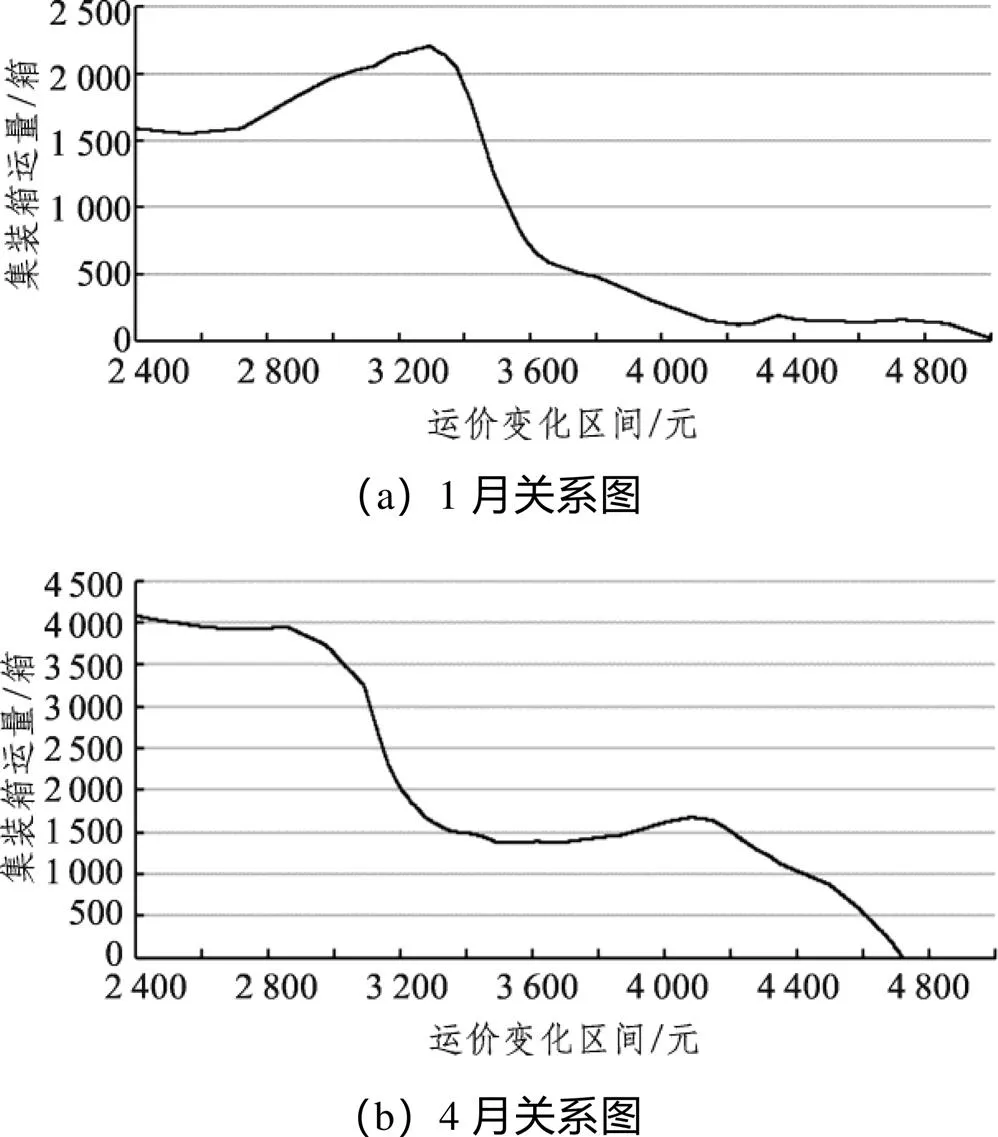
图6 运价与集装箱需求关系图
如图6可知:
(1)运价和运量的整体趋势是随着价格的上升运量下降,但并不是光滑的负相关函数。且运量在运价增加时有小范围上升,反映了需求上升的时候价格也上升的经济现象。对此传统需求函数较难描述和预测此类市场变化,而LSTM深度学习网络能挖掘出此类潜在的市场现象。
(2)不同月份运价的变化对应不同的运量变化区间和趋势,说明不同时间客户对运价的敏感度不同,因此运输需求无法用某一固定参数函数进行描述。
4.2 定价模型求解及结果分析
根据目前该路局的运营计划,该路局每月更新一次集装箱运输定价,12个月为一个决策周期。使用第3节中建立的基于精英选择策略的遗传算法与LSTM网络反馈机制,将上述已分别训练的LSTM网络接入基于精英选择的遗传算法端口。在运价上下限区间[2 400, 5 000]中随机生成运价并输入LSTM网络中,然后输出对应的集装箱货运需求。遗传算法种群规模设置为50,最大遗传代数为500。在遗传算法模块并行计算优化上述OD,输出不同区间上不同货物在不同时间的集装箱运输最优定价及总收入、利润。
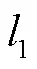
由图7可知,目前铁路运价还有较大的调整空间,在运营前期制定价格时可采取适当向下调整运价的策略,以吸引客源;当运输旺季时可适当提升价格,控制需求来减少运输成本进而提升收益。
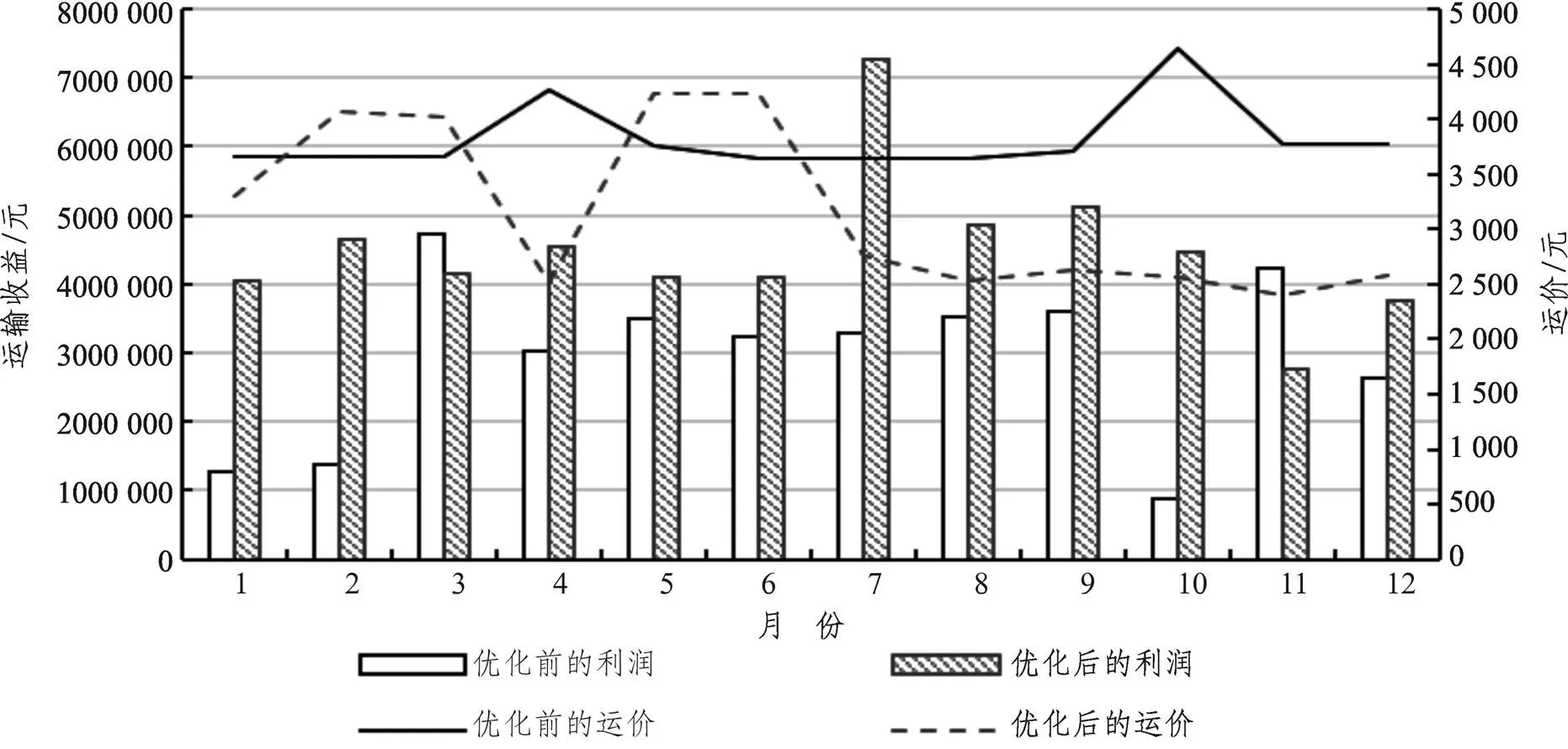
图7 优化前后对比图
5 结 论
本文通过线性、logit模型与LSTM神经网络深度学习模型对铁路集装箱需求进行拟合,实验发现线性、logit函数等参数函数由于其参数的有限性,对真实市场的拟合情况不佳。而LSTM深度学习模型的历史数据在测试集中误差最小,可挖掘市场潜在的变化趋势和各因素的变化关系,拥有较好的泛化能力。案例分析表明基于深度学习需求模型的动态定价策略可用于企业需求管理,挖掘出不同时期需求的价格弹性,制定更加合理的价格策略。在接下来还可针对当日实时定价进行研究,将天气、客户浏览、节假日等信息纳入深度学习模型的训练,进一步探究市场变化和客户行为,优化日定价策略。
[1] 刘清芳. 铁路集装箱运输发展对策探讨[J]. 铁道运输与经济, 2020, 42(9): 34-39.
[2] TALLURI B, RYZIN G. The theory and practice of revenue management[M]. Berlin: Springer, 2005.
[3] 姜爱萍, 夏浩, 高峻峻, 等. 电力物资复合泊松需求下的最优订货量[J]. 工业工程, 2016, 19(3): 90-95.
[4] GRAF M, KIMMS A. An option-based revenue management procedure for strategic airline alliances[J] European Journal of Operational Research, 2011, 215(2): 459-469.
[5] 宋文波, 赵鹏, 李博. 高速铁路单列车动态定价与票额分配综合优化研究[J]. 铁道学报, 2018, 40(7): 10-16.
[6] GALLEGO G, RYZIN G V. Optimal dynamic pricing of inventories with stochastic demand over finite horizons[J] Management Science, 1994, 40(8): 999-1020
[7] 方园, 乐美龙. 基于强化学习的平行航班动态定价[J]. 华东交通大学学报, 2020, 37(1): 47-53.
[8] 文书生, 叶怀珍. 基于VAR模型的中国铁路集装箱需求实证分析[J]. 重庆大学学报: 自然科学版, 2007(10): 152-158.
[9] 张立欣, 张艳波, 杨翠芳. 基于X11-ARIMA模型的铁路集装箱周转量分析[J]. 数学的实践与认识, 2018, 48(17): 154-161.
[10] 景楠, 史紫荆, 舒毓民. 基于注意力机制和CNN- LSTM模型的沪铜期货高频价格预测[J/OL]. 中国管理科学: 1-13[2020-10-13]. https: //doi. org/10. 16381/j. cnki. issn1003-207x. 2020. 0342.
[11] XU H, SUN H, NIKOVSKI D, et al. Learning dynamical demand response model in real-time pricing program[C]// 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference(ISGT), Washington: IEEE, 2019: 1-5.
[12] 王鑫, 吴际, 刘超, 等. 基于LSTM循环神经网络的故障时间序列预测[J]. 北京航空航天大学学报, 2018, 44(4): 772-784.
[13] 张小强, 刘丹, 陈兵, 等. 竞争环境下铁路集装箱班列动态定价与开行决策研究[J]. 铁道学报, 2017, 39(2): 17-23.
[14] 高醒, 李夏苗, 彭鹏. 铁路货运量预测过程中的关键技术分析[J]. 科技和产业, 2018, 18(5): 1-8, 62.
Research on Dynamic Pricing of Railway Containers under Uncertain Demand
TANG Hui-min1, TAN Xue1, ZHANG Xiao-qiang1, LIANG Yue2
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. Transport and Urban Planning and Design Research Institute, China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China)
In this study, the traditional linear demand function and the multi-logit demand model with the deep learning demand model, based on the long short-term memory (LSTM) neural network, are compared, considering the uncertainty of the railway container transportation demand model. This study maximizes the profit of the railway carrier by establishing a dynamic container pricing model. We extract the feature vectors related to the container freight demand, use the gradient descent method to solve the linear function and logit model parameters, and train the LSTM neural network through the supervised learning method. The results show that LSTM is more accurate relative to demand than linear and the logit function. We design an e-GA combined with the dynamic pricing feedback mechanism of LSTM to solve the pricing model. Finally, calculations based on actual cases show that the dynamic pricing model of railway containers based on LSTM can effectively increase the revenue of railway freight enterprises.
railway transportation; dynamic pricing; demand model; revenue management; long short-term memory
1672-4747(2021)03-0133-10
U294.3;F532.5
A
10.19961/j.cnki.1672-4747.2020.10.005
2020-10-13
2020-12-09
2021-06-28
四川省科技厅软课题(2020JDR0127);成都市科技局软科学课题(2020-RK00-00102-ZF)
唐慧敏(1996—),女,汉族,四川眉山人,硕士,研究方向为铁路运输、深度学习,E-mail:744766576@qq.com
张小强(1975—),男,汉族,江西石城人,副教授,研究方向为铁路运营管理、人工智能,E-mail:xqzhang@swjtu.edu.cn
唐慧敏,谭雪,张小强,等. 不确定需求下铁路集装箱动态定价研究[J]. 交通运输工程与信息学报,2021, 19(3): 133-142.
TANG Hui-min,TAN Xue,ZHANG Xiao-qiang, et al. Research on Dynamic Pricing of Railway Containers under Uncertain Demand [J]. Journal of Transportation Engineering and Information, 2021, 19(3): 133-142.
(责任编辑:李愈)
