散装机伸缩段粉煤灰流动特性分析
2021-09-11中电国瑞物流有限公司淮南分公司安徽理工大学机械工程学院来永斌张文龙
中电国瑞物流有限公司淮南分公司 毕 波 安徽理工大学机械工程学院 来永斌 王 龙 张文龙
粉煤灰作为发电废料在化工行业得到广泛利用,然而粉煤灰的输送和储存是一项复杂的研究内容。相比各种输灰方式,气力输灰具有结构简单、持续大量输送和抗环境干扰强等优点被大量专家研究。尹莉钧[1]针对输灰能耗问题,以贝叶斯理论为基础进行了单管测模型,分析了粉煤灰的灰气比和气流速度对粉煤灰生成的影响,并通过数值模拟结果整合的数学模型对输灰系统进行优化;万承军[2]对正压输灰系统进行了系统性的实验研究,提出了灰气比及单位能耗与输送距离间的关系公式,根据所得公式指出输灰单位能耗随距离增加而减小。
李志学[3]在管道气力输灰中,针对管内介质高速流动磨损管壁导致的问题管道破坏泄露、增加空压机数量和输灰用气的用量的问题,应用了先导式气力输灰系统。使用改造的输送系统在用气量节约七成的同时节约空压机的使用数量,从而减少输灰能耗;丛相州[4]运用实验和数值模拟研究输灰管道的弯头处颗粒磨损的行为,验证了耐磨堆焊层在管道输灰中具有更高的耐磨性,使用该方法可大大提高管道的使用寿命;厉复军[5]为解决布袋排灰堵塞造成的间歇修整问题,通过实验分析现有的输灰系统并进行优化,指出增加布袋输灰管道水平位置和缩短管道距离等措施降低输灰管道堵塞问题。
刘毅[6]运用实际工程验证理论和公式推导对正压浓相输灰系统进行研究。通过实验获取了60个工程数据,并进行公式拟合获得了管道输灰管径与其他因素的数学关系模型,为工程中输灰管径设计提供参考;李荫堂[7]在研究中将灰气划分为稀、中和浓相,通过实验提取中浓度的灰气的压降数据,并将大量管道压降数据拟合成数学模型,该数学模型可表示粉煤灰输送管道中浓度区的总压降与阻力系数的关系,通过拟合式可知物料质量流量和灰气比对阻力系数的影响变化较小;袁宝强[8]采用Tabakoff 冲蚀模型建立灰气的Fluent 多相流的磨损和沉积UDF 模型,进行灰气对换热管束的磨损和沉积数值模拟研究。得出结论包括灰气对圆管的磨损比椭圆管的磨损大、飞灰粒径越大对管壁的磨损越严重、管的最大磨损在迎风面、较高流速的小飞灰颗粒在背风面的沉积更大等。
以上研究集中在管道中流动损失磨损等问题,从现有文献看,对工程实际问题中的粉煤灰灌装漏灰低效率问题鲜有提及,本文通过对实际装置进行改进,运用多相流理论分析其内部流动特性,最终设计出新型结构,达到“防漏”“高效”目的,解决实际工程问题。
1 模型简介
粉煤灰罐模型按照实际尺寸进行设置(图1),由内外管道和灰罐车箱体组成。内管为下料管,外管为吸尘管,吸尘管用于回抽灰罐车内部空气和少量被空气带出的粉煤灰。灌装管道与灰罐车之间有一段是可伸缩的,用于与灰罐车进料口相连进行灌装。伸缩段下料管由多个锥环构成,吸尘管为布袋(图2)。由于在灌装时各锥环间存在较大间隙,粉煤灰在下落过程中从间隙被吸尘管回抽到上部的布袋除尘器中(图3),不能完全落入灰罐车箱体,造成灌装效率下降、吸尘风机功率增大、布袋除尘器使用寿命降低。同时过多的回抽粉煤灰造成灰罐车内压增大、导致冒灰现象产生,且在伸缩段提升过程中产生漏灰,造成环境污染。为提高工作效率、减少粉煤灰逃逸量,本文建立三种不同的散装机伸缩段结构模型(图2、图4、图5),通过数值模拟,分析粉煤灰在不同结构装置内的流动状态,确定满足工作要求的优化结构,解决实际工程问题。

图2 原伸缩段结构示意图
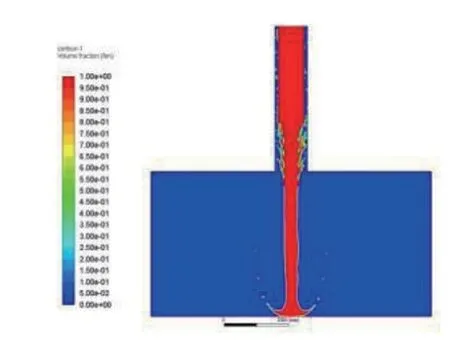
图3 原始装置粉煤灰流动图
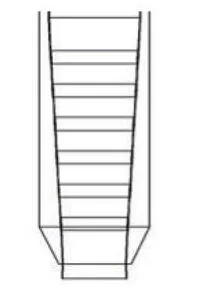
图4 密封收缩内伸结构

图5 密封收缩平口结构
流场边界条件以及参数设定。入口边界条件:采用质量流量入口90kg/s;出口边界条件:流场域的出口设定为压力出口,为观察粉煤灰在内外管道内的逃逸量。设置为负压,数值为-200Pa;壁面条件:内外管道壁面及罐车箱体设定为无滑移壁面。以上边界条件具体设定如图6所示。本文采用Mixture 混合模型,相数为2,分别为粉煤灰和空气,模型划分采用四面体网格进行划分,网格单元总数近200万(图7)。

图7 网格划分图
2 数值模拟分析结果
2.1 不同结构的粉煤灰速度分布对比
图8~10为不同模型下粉煤灰速度分布图,图8速度分布可知,在粉煤灰下降过程中,原始模型由于收缩内管的存在使得下降速度有所变化。不同于在直管中自由下落,粉煤灰颗粒在锥环间隙处积聚,从而使得下降流量降低,影响粉煤灰实际生产输送量。图9~10为提高粉煤灰灌装效率和减少粉煤灰逃逸设计的模型,模型采用向下收缩结构,锥环直径不断减小,当散装头与灰罐车进料口接触时,下料管下落伸长、上级锥环内壁和下级锥环外壁贴合,锥环之间不存在间隙,杜绝了粉煤灰在下落过程中被回抽到吸尘管,与原始模型相比灌装效率明显提高。
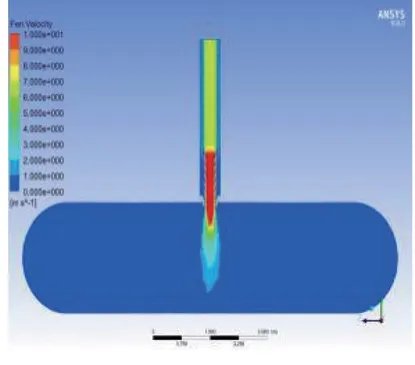
图8 原始模型粉煤灰速度分布图
图9和图10的模型下料管出口长度不同,改变了粉煤灰在管道末端的流动状态。从粉煤灰进入罐车的速度分布来看,内伸模型要大于平口模型,从流量的角度可更快地完成灌装工作。两种模型在吸尘管均没有粉煤灰逸出,相对于原始模型灌装效率都得到提高。图9所建立的模型结构更能满足使用要求。

图1 粉煤罐装示意图
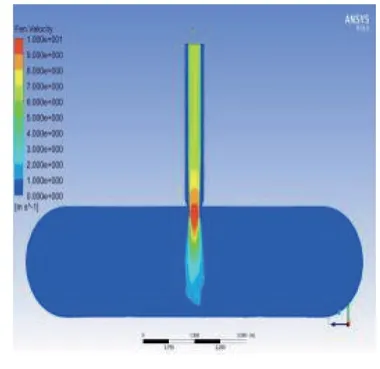
图9 密封收缩内伸模型粉煤灰速度分布图
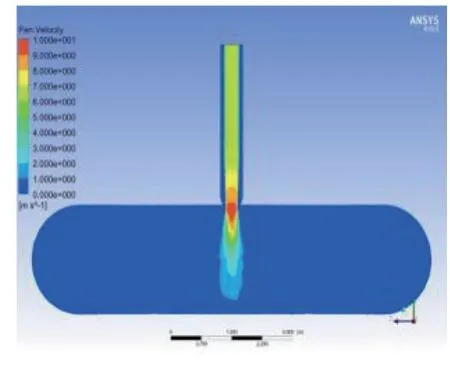
图10 密封收缩平口模型粉煤灰速度分布图
2.2 不同结构的粉煤灰体积分布对比
图11~13为不同结构模型的粉煤灰体积分布图。通过粉煤灰在流动过程中的体积分布,可直观看出粉煤灰分布的具体位置。图11为原始模型的粉煤灰体积分布,粉煤灰在下降过程中,经由锥环外溢较多,由于内外管道间压差的存在会造成外溢的粉煤灰挤压至吸尘管出口处,这样会导致粉煤灰灌装效率降低。
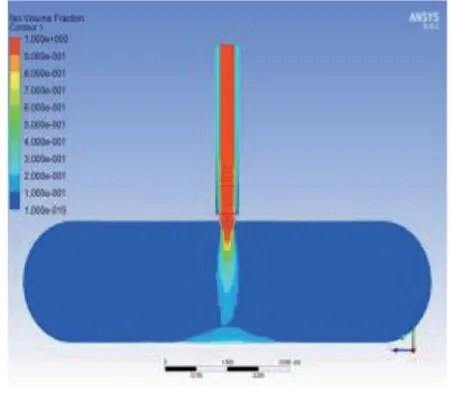
图11 原始模型粉煤灰体积分数分布图
图12和图13为改进模型后的粉煤灰体积分布。由图可知模型结构采用密封结构时,粉煤灰在内外管道间距内的体积分数明显减少,粉煤灰溢出量很少。改进后的模型均在内管道末端出现粉煤灰“喷射散开”现象。图14为局部放大的密封收缩模型粉煤灰体积分数分布图,为更好地对比粉煤灰逃逸情况,把体积比率设置为0~0.15之间,从图中可清晰看出内伸模型在吸尘管内几乎不存在粉煤灰,而密封平口模型会存在一定量的粉煤灰从吸尘管进口逸出,其值约在0.035,但仍优于原始模型。从图14(a)和(b)对比可知,在单位时间内密封内伸模型的粉煤灰灌装效率最高。密封收缩内伸模型既杜绝了粉煤灰经由锥环间距的回抽现象、控制粉煤灰的逃逸,又提高粉煤灰的灌装效率、降低了生产能耗。

图12 密封收缩内伸模型粉煤灰体积分数分布图

图13 密封收缩平口模型粉煤灰体积分数分布图
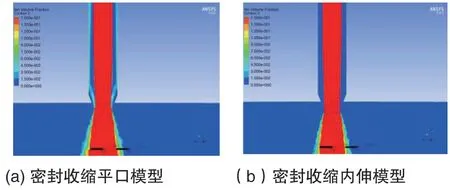
图14 密封收缩模型粉煤灰体积分数分布图(局部放大)
3 结论
本文利用数值模拟方法对不同结构的散装机伸缩段粉煤灰灌装过程进行分析,通过对比三种结构,分析结论如下:对于原始模型结构,粉煤灰在灌装过程中存在粉煤灰回抽现象,较多粉煤灰从吸尘管进入布袋除尘器内,造成灌装效率下降,除尘布袋的使用寿命降低;密封收缩内伸模型的设计既杜绝了粉煤灰经由锥环间隙的回抽现象、控制粉煤灰的逃逸,又提高了粉煤灰的灌装效率、降低了生产能耗,对实际生产具有很大的实用价值。