复杂系统的同步稳定性研究
2021-09-11孙启阳
孙启阳
(广东工业大学,广东 广州 510000)
1 概述
随着科技水平的提高和技术融合的发展,复杂系统近年来逐渐走进了人们的视野,并且越来越受到人们的关注。因其具有资源共享、系统简便、容易构建、灵活性强等优点,因而广泛应用于诸如互联网以及通信领域、交通领域、智能制造领域、航空航天等各个领域。在实际控制中,因系统各个节点所面临不同的情况以及其中不同节点之间的通信延迟,常会影响到系统的稳定性,进而对系统的工作效率产生不良影响。由于复杂系统的广泛应用以及其所具有很高的研究价值,因而吸引了国内外很多研究人员对此进行研究,并且在复杂系统的一致性问题研究这个方向上做了更深一步的探索。
2 理论推导
首先考虑如下单个节点的状态方程:

利用克罗内克积整合多个节点的状态方程,可以得出该复杂系统的状态方程为:
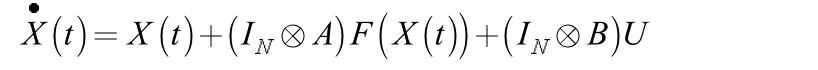
为了使系统达到同步稳定,并且减轻网络拥堵情况的发生以及减缓控制器的输出频率,以此来降低控制系统所需要的网络资源,我们为每一个节点都设置了采样数据控制器:

因此可知,若给定一个满足条件的强连通有向图G(A),给出合适的系统增益矩阵K,如果存在实矩阵U>0,P>0,P2>0,P3>0,P4>0,使得对任意的输入条件,均有下列不等式成立,则说明该复杂系统能够实现同步。


3 模拟仿真
本章将提出一个仿真实例来验证所提理论结果的有效性,利用仿真实验对所设计的控制器和控制方法进行应用。复杂系统的拓扑结构如图1 所示。

图1 复杂系统的拓扑图


针对某个节点i 的采样数据控制器的步骤如下:在采样时间,节点i 与其他节点之间按规则进行通信,发出或接收节点信息;如果节点i 接收到来自其他节点的信号,则它对应的控制器将执行算法;控制输入信号在相邻采样时刻之间保持恒定,数值等于前一个采样时刻的控制输入信号;在下一个采样间隔重复上述三个步骤。
将系统的耦合强度表示为α,将系统的饱和水平表示为Uil。根据系统的采样控制器可以明确,最大采样上界并不会影响到 的数值大小。所以不妨假定α=0.5,Uil=0,因为系统由五个节点构成,因此l=1,2,3,4,5,即U 具有五个数值。通过使用ode45,解出线性矩阵不等式方程组可以得到:

系统的采样上界为h2=0.9,进一步的,以下是五个节点在仿真实验下得到的状态轨迹:
根据图2 可以看出,上文中所构建复杂系统中的五个节点的状态轨迹随时间增长而逐渐趋于一致,即系统将达到同步。

图2 五个节点的状态轨迹
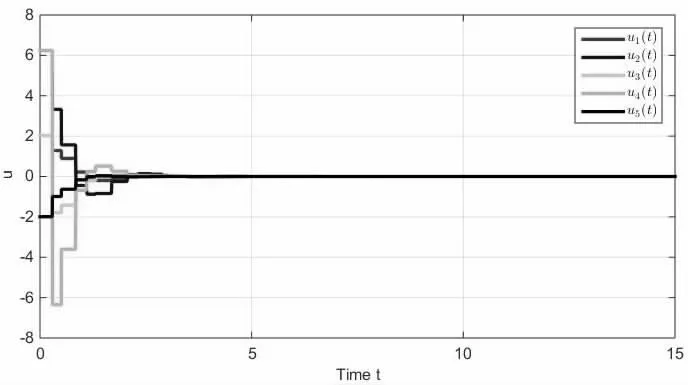
图3 五个节点的采样数据控制输入

根据图4 可知,随着时间的增长,五个节点的系统同步误差在控制器的作用下逐渐衰减直至归零。其实际意义为各个节点状态最终将完全相同,即系统达到同步稳定状态。

图4 五个节点的系统同步误差
4 结论
复杂系统在实际生活中应用广泛,因此具有很高的研究潜力和价值。本文利用李雅普诺夫定理,研究了采样数据控制下的含有非线性项的复杂系统的一致性问题。本文构造了一个全新的李雅普诺夫泛函,并通过理论推导与模拟仿真对其效果进行了验证,证明了该函数的合理性有和效性。
