不同锭型及热负荷下均热炉内对流换热系数的模拟分析

王正洁，谭秋生，苏福永

(1.青岛特殊钢铁有限公司，青岛 266409;2.北京科技大学能源与环境工程学院，北京 100083)

0 引 言

均热炉的主要作用是在初轧前把钢坯加热或保温一定时间，通过热扩散使钢锭内部温度均匀从而适于金属塑性加工用的室状炉[1-3]。均热炉是初轧生产中的重要加热设备。它将来自炼钢厂的冷、热钢锭均匀地加热到轧制所要求的温度，并连续地供给初轧机进行轧制[4-5]。均热炉炉膛为长方体形，钢锭在炉内竖放，通常由几个炉坑组成一组，共用一套控制系统。蓄热式均热炉作为目前广泛应用的一种炉型，其炉坑两端有蓄热室，因其换向供热带来炉内流场复杂的周期变化，从而引起炉内对流换热系数的大幅变化，最终影响钢锭在炉内的换热过程[6-7]。

在蓄热式均热炉炉内换热的研究过程中，随着计算机的发展和蓄热室研究的逐步深入，数值模拟研究逐渐成为一个重要方向。国内外学者采用数值模拟的方法对蓄热式燃烧过程的流场、燃烧温度、蓄热式均热炉内换热过程等进行了大量仿真研究，为蓄热式均热炉的发展做出了贡献[8-10]。

本文针对不同热负荷下蓄热式均热炉内的对流换热过程开展数值模拟研究，通过对不同热负荷下炉内钢锭表面对流换热系数的变化分析蓄热式燃烧方式对均热炉内钢锭加热的影响，为蓄热式均热炉的工艺优化提供基础。

1 物理模型及数学模型

1.1 物理模型

本文的数值模拟研究对象包含均热炉炉膛以及炉内钢锭，其示意图如图1所示。其中炉长、炉宽和炉高分别为7 900、4 000、5 000 mm。各模拟主要锭型尺寸见表1。

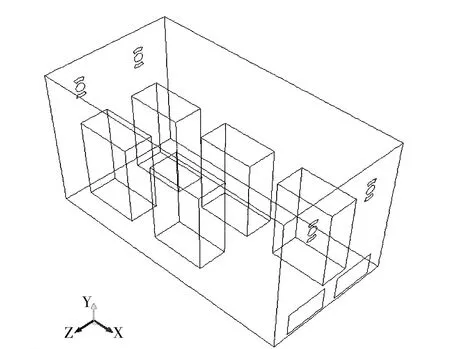
图1 蓄热式均热炉物理模型示意图

表1 主要锭型参数表

1.2 数学模型

本文主要针对均热炉加热不同钢锭时的对流换热过程进行模拟，以此来求得不同工况下、不同钢锭在炉内的对流换热系数。在进行模拟工作之前，本文做出了如下假设。

(1)在实际生产过程中炉压变化不大，因此假定气体为不可压缩流体；

(2)根据均热炉的特点，假设炉顶、炉壁以及炉底为等热流边界；

(3)钢锭外表面的初始温度相同。

基于以上假设，本文的控制方程包括：

连续性方程：

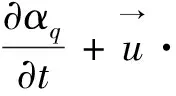
(1)

能量方程：

(2)

动量方程：

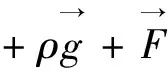
(3)

湍流模型采用标准k-ε模型，控制方程如下：

+Gb-ρε-YM+Sk

(4)

(5)

本文在模拟过程中采用非预混PDF燃烧模型；辐射换热过程采用DO模型。

2 模拟结果分析

在煤气热值6 700 kJ/m3，最大煤气流量4 320 m3/h，炉温给定值为1 300 ℃时，本文选取了五种最具代表性的工况来进行模拟，模拟时所选取的空煤气入口速度见表2。

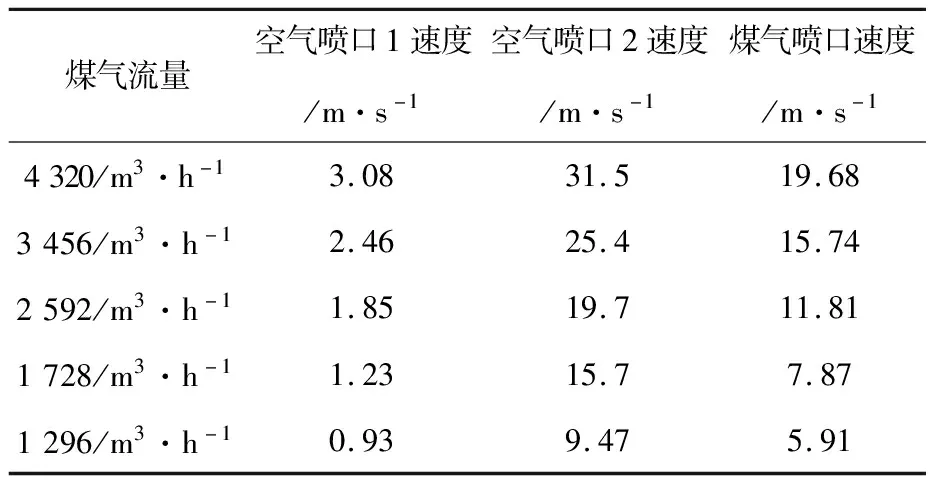
表2 各喷口气体的喷射速度

模拟结果中炉内速度场云图及矢量图如图2-图4所示(以3300锭型加热时煤气流量4 320、2 592、1 296/m3·h-1为例)，在不同热负荷的条件下，炉内的流场趋势基本相同，随着热负荷的减小，空气及煤气的入炉速度明显减小，火焰对于炉气的搅拌作用也在逐渐减弱。

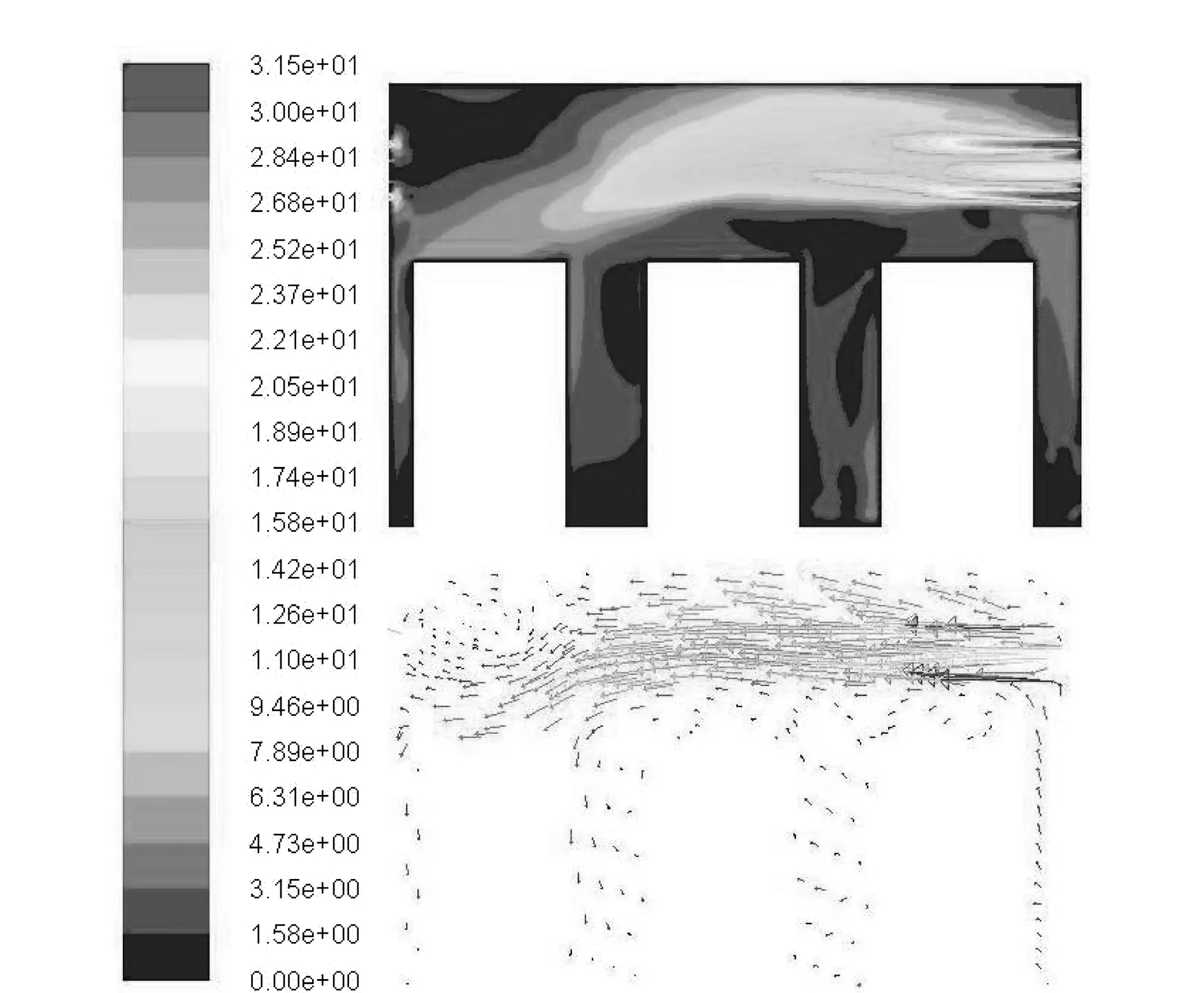
图2 热负荷为4 320 m3/h(100%)时炉内速度场云图及矢量图

图3 热负荷为2 592 m3/h(60%)时炉内速度场云图及矢量图

图4 热负荷为1296m3/h(30%)时炉内速度场云图及矢量图

(1)加热3300锭型时蓄热式均热炉内对流换热系数随热负荷的变化规律

3300锭型时蓄热式均热炉内不同热负荷情况下的对流换热系数见表3。

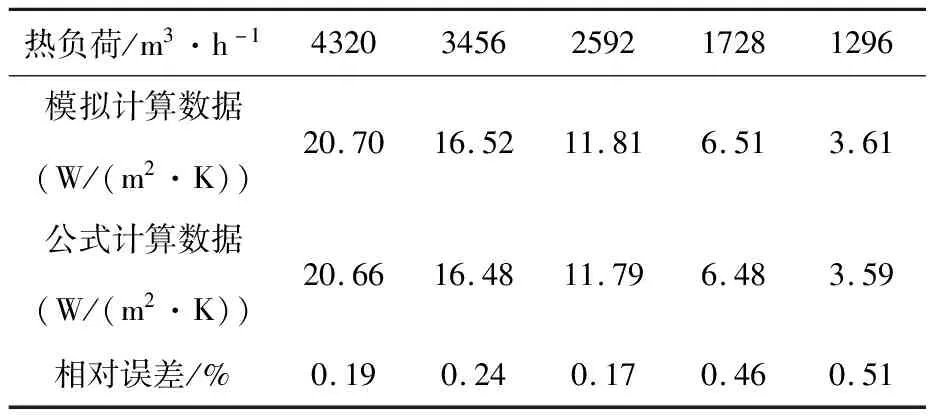
表3 3300锭型不同热负荷对应的对流换热系数(W/(m2·k))计算结果

根据表3中的模拟结果，采用数据回归技术求出钢锭表面Nu数回归关联式，见式(6)，对流换热系数公式见式(7)。

Nu=1.97*10-5Pr0.33Re1.44

(6)

式中，Pr为普朗特数；Re为雷诺数。

α=λfNu/dp

(7)

式中，α为对流换热系数，(W/(m2·K))；λf为烟气的导热系数，W/(m·K)；Nu为Nusselt数；dp为烧嘴二次风口处当量直径，m。

在得到该回归关联式后，本文用该公式计算得到的换热系数也列在了表2中，由回归公式计算所得对流换热系数与模拟值相比最大相对误差仅为0.51%，回归公式的计算精度满足要求。

(2)加热6110锭型时蓄热式均热炉内对流换热系数随热负荷的变化规律

6110锭型时蓄热式均热炉内不同热负荷情况下的对流换热系数见表4。

表4 6110锭型不同热负荷对应的对流换热系数(W/(m2·k))计算结果

利用表4中的模拟计算数据，采用数据回归技术可以求出Nu数回归关联式，见式(8)。

Nu=6.21*10-5Pr0.33Re1.53

(8)

通过回归关联式计算所得到的对流换热系数也同时列出在表4中，可以看到，回归关联式最大相对误差为0.39%，准确性较好。

(3)加热8920锭型时蓄热式均热炉内对流换热系数随热负荷的变化规律

8920锭型时蓄热式均热炉内不同热负荷情况下的对流换热系数见表5。

表5 8920锭型不同热负荷对应的对流换热系数(W/(m2·k))计算结果

利用表5中的模拟计算数据，采用数据回归技术可以求出Nu数回归关联式，见式(9)。

Nu=2.33*10-5Pr0.33Re1.84

(9)

通过回归关联式计算所得到的对流换热系数也同时列出在表5中，可以看到，回归关联式最大相对误差为0.37%，准确性较好。

3 结束语

本文模拟了锭型为3300、8920以及6110三种主要锭型钢锭在不同热负荷下炉内钢锭对流传热过程，得到不同热负荷下钢锭表面的对流换热系数，通过回归分析，得到了使用煤气热值为6 700 kJ/m3情况下，各主要锭型对流换热系数与热负荷之间的回归关联式。本文研究所得成果为蓄热室均热炉炉内钢锭温度计算提供了必要的计算参数，为均热炉的工艺优化奠定了基础。