《正方体截面的形状》教学设计

刘晓挺 颜甄璞 宋天娇 刘京安 马飞飞

一、内容简介

本课例定位北师大版数学必修二第一章课题学习《正方体截面形状》，以正方体截面为核心，让学生通过小组合作学习的方式，观察、猜测、实践、探究，通过尝试归纳，类比总结发现有关截面问题的知识点和学习方法，教师在教学过程中进行必要的指导，培养学生在立体几何知识中的探究能力，解决直观想象中如何引导学生如何通过“直观”进行“想象”的问题，实践落地高中立体几何教学中学生“直观想象”核心素养的培养问题。

二、教学目标

正方体是立体几何中的万能图形，本节课设计平面“切”正方体的项目式教学，基础目标是通过学生动手实践和观察，更好的直观理解几何体中点线面的位置关系，通过对点线面位置关系的理解，了解正方体截面多样性的原因。主旨目標是希望通过“观察——猜想——实验——验证——总结”的过程，培养学生空间想象、动手实践、合作交流、分析判断、推理论证、探索创造的能力，培养学生空间想象意识，落实“直观想象”等数学学科核心素养的培养。

三、教学重点

正方体截面形状的感观认识，总结截面图的性质，利用相关几何公理、定理构造截面图。

四、教学难点

掌握截面图构造方法、发现规律，并能用规律解决问题。

五、教法学法

启发引导式教学、自主学习、探究学习、合作学习

六、课前准备：

（正方体）萝卜块若干、美工刀、PPT等。

七、教学过程：

（一）情境引入

PPT视频：厨师切土豆，不同方式切出不同样式。

问题1：什么叫几何体的截面？

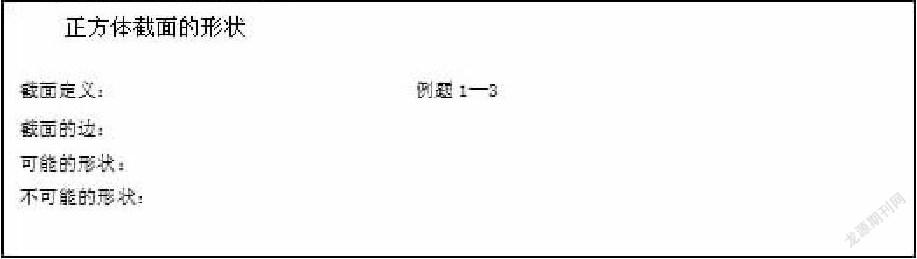
截面定义：在立体几何中，截面是指用一个平面去截一个几何体，得到的平面图形，叫截面。

问题2：截面的边是如何得到的？

截面的边：平面和几何体各面的交线。

（二）讲授新课

问题3：正方体是立体几何中一个重要的模型，如果我们用平面去“切”一个正方体，那么我们得到截面都有什么形状？截面最多有几条边（给出分类原则）？

三角形、四边形、五边形、六边形等。

（设计意图：通过“切”引发学生对截面形状的思考，尝试激活直观想象能力，激发学生学习兴趣，为动手实践做好准备。）

教学活动：学生分组切萝卜实验

要求：1.两人一组（以同桌一组为宜）

2.先大胆猜想，再实践操作，分析原因，最后做好记录和总结。

3.注意安全，勿划伤手指。

问题4：大家能“切”出什么形状的截面（学生演示切的成果）

（设计意图：引导学生对各种截面进行分类，进一步思考截面背后的原因，即如何能截出这样的图形）

问题5：如何“切”，使得截面成三角形，其构成形状有哪些？（学生先想象，在实践，教师尝试引导学生总结规律：用一个平面截正方体一个角构成，平面经过正方体的三个面时，那么截面就是三角形。）

思考交流：能切出直角三角形、钝角三角形么？为什么？

（设计意图：进一步从直观图形中感知图形背后的原因，引导学生讨论、分析出截面的成因，从教学中落地直观想象不是只是看图或者数形结合，更重要的是通过图去理解知识、归纳总结）

问题6：从三角形进阶到四边形→如何切，使得截面成四边形，其构成形状有哪些？（学生演示切的成果）

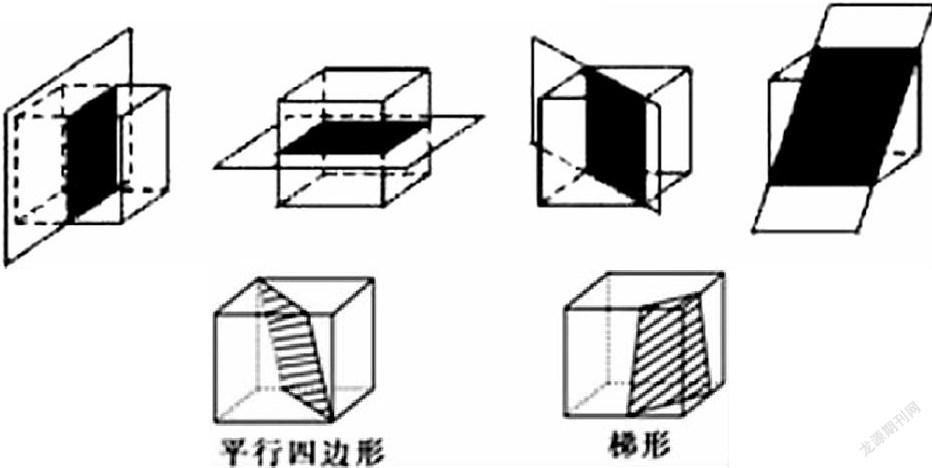
当切面经过正方体的四个侧面时，所得截面可能是正方形、长方形、平行四边形、梯形。

思考交流：能切出任意四边形、直角梯形么？为什么？

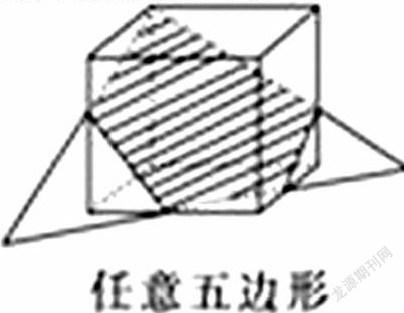
问题7：如何“切”，使得截面成五边形？

当平面经过正方体的一个顶点和其它四条棱时，所得截面是五边形。

思考交流：能切出正五边形么？

问题8：如何“切”，使得截面成六边形？

当平面经过正方体六条棱时，所得的截面是六边形。

思考交流：能切出正六边形么？能切出七边形么？为什么？

（问题6-8设计意图：一生二、二生三，三生万物，引导学生通过类比和在脑海中进行“想象”，再通过观察直观图形和实物实践的方式进行验证，最后对截面进行量化小结，完成对学生直观想象的核心素养培养）

（三）总结交流

可能出现三角形：锐角三角形、等腰三角形、等边三角形。

四边形：正方形、矩形、非矩形的平行四边形、非等腰梯形、等腰梯形。

五边形、六边形、正六边形。

不可能出现钝角三角形、直角三角形、直角梯形、正五边形、七边形、更多边形

（设计意图：让学生经历数学知识的生成过程，再进行小结，完成从感性到理性的过程，借助几何直观图形和空间想象来感知事物形态与变化，培养学生学科核心素养。）

（四）例题讲解

例1：木工在处理如图所示的一块正方体木料时，发现木料表面有一块裂纹，他打算沿裂纹将木料锯开，却不知道如何画线，你如何帮他解决问题？

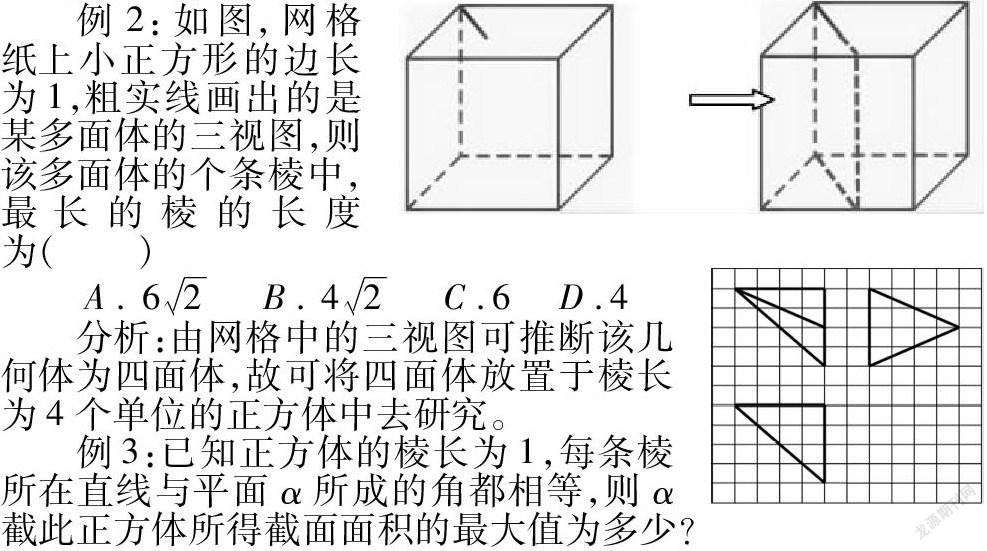
例2：如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为（ ）

A.62 B.42 C.6 D.4

分析：由网格中的三视图可推断该几何体为四面体，故可将四面体放置于棱长为4个单位的正方体中去研究。

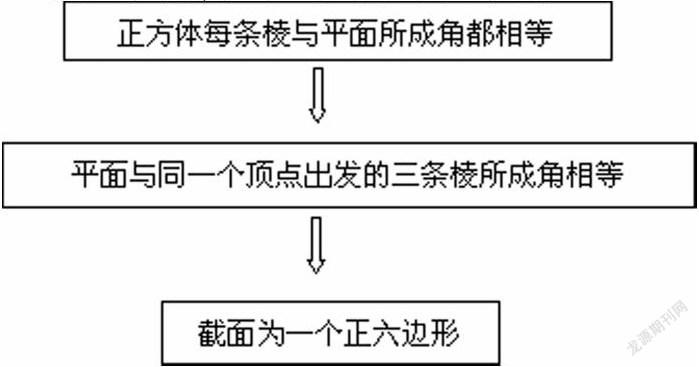
例3：已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为多少？

分析：

由此推断截面与棱交点为棱中点，最后可根据6个全等三角形面积公式求得。

（例题设计意图：通过例题联系知识点，发现立体几何中点、线、面、角之间的关系，借助正方体直观图解决问题，考察学生直观想象能力的具体掌握情况）

（五）课堂小结

让学生畅所欲言，说学到的数学知识、数学思想方法;说学习方法、学习体会，逐步养成归纳总结的习惯。

（六）课后作业：

作业1：写一份学习报告。

作业2：截面问题课后拓展（开放题）

制作三棱锥、柱、台几何体实物。

如果用平面“切”其它几何体（长方体、棱锥、棱台、圆锥、圆柱等），其截面是什么图形？如果截面是已知常规图形（长方形、三角形），则原被截的几何体可能是什么？

（设计意图：举一反三，培养学生学会学习的能力）

（七）板书设计：

1 陕西省碑林教师进修学校 2 西安市第二十六中学太乙分校 3 西安市第八十二中学4 西安市第六中学 5 西安市第三中学