基于模式识别PI自整定的 漆包线点焊智能控制

田然 曾家铨 刘明 曹彪 黄增好

摘要：漆包线点焊过程时间较短，要求点焊电源控制响应快速，且其电极具有属性差异大、在使用过程中因不断损耗需频繁更换的特点。常规PID控制由于其参数固定不变，难以根据点焊回路尤其是电极差异进行自适应调整。提出一种基于模式识别PI自整定的漆包线点焊智能控制方法，与常规PID控制方法相比，该方法可针对不同的电极对控制参数进行自整定，提高了漆包线点焊控制的稳定性和快速性，取得了较好的应用效果。

关键词：漆包线点焊;PID自整定;模式识别;智能控制

中图分类号：TG409         文献标志码：A         文章编号：1001-2003（2021）01-0049-05

DOI：10.7512/j.issn.1001-2303.2021.01.07

0    前言

漆包线广泛应用于电子和电气等领域，常作为元件内外连接的导体介质或绕成线圈作为元件的一部分。单面电阻点焊是目前常用的一种漆包线点焊方法，一般采用具有特殊回路结构的点焊电极，通电时，电极端部电流密度大，电流热效应使端部极速升温至红热状态，从而实现漆包线的脱漆与焊接[1-3]。

漆包线点焊一般采用基于PI控制的恒电压模式，有时也采用恒电流模式，但目前常见点焊电源的单一固定PI参数无法较好地适应漆包线点焊电极的以下几个特点[4-5]：（1）不同形状、大小、材质的电极差异较大，比如存在片状电极与针状电极;（2）使用过程中，端部损耗对回路影响较大;（3）更换频繁，自动化产线一天就可能消耗数支电极，即便仅应用同一种电极，由于电极端部尺寸较小，难以保证较好的材料均匀性和加工一致性。

因此，为了保证不同电极甚至同一电极不同状态下在电源输出过程中不会产生震荡或较大的过冲，一般控制策略较保守，选取的PI参数较小，造成阶跃响应在约3～6 ms区间内达到设定的电压值，响应的一致性难以保证，并且较难适应短时间快速焊接的需要。即便采用较保守的控制策略，随着电极的损耗、电阻的不断增大，在电极寿命的中后期仍然可能发生震荡。因此，需要针对不同电极甚至同一电极的前后不同状态进行PI参数的自整定并智能监控。

1 控制系统结构与模式识别法

设计了如图 1所示的逆变式电阻点焊电源控制器，其输入端为焊接回路的电压或电流反馈信号，经过采样电路的信号处理输入到PIC32MK芯片的ADC端口，再经过PI控制，输出PWM信号，PWM信号经过驱动电路隔离放大后控制IGBT，从而控制焊接回路。

漆包线点焊使用电极具有特殊的回路结构，不论有无焊接工件，点焊回路都是完整的。在电源放电前期，漆包线漆皮未熔化，对回路控制影响较小，焊接所需热输入主要靠电极传热，漆皮熔化后才可能发生分流。因此，对PI控制效果的检验可以选择在无工件情况下进行阶跃响应测试。

一般自整定方法都需要对过程模型进行辨识，计算复杂。而模式识别法可以避开过程模型问题，且无需像继电反馈法那样产生自激振荡，在闭环系统阶跃响应波形上选取一组能表征过程特性且数据量尽可能少的特征信息作为状态变量，以此为依据设计自整定方法，属于智能PID控制[6-8]。

文中的阶跃响应下基于模式识别的PI自整定控制器原理如图2所示。原理为：对阶跃响应系统误差e的时间特性进行模式识别，提取该过程部分特征参数ek作为状态变量，将其与理想模式的状态变量值进行比较，按大小关系送入基于二分法的自整定算法环节，计算出PI控制器各参数所对应的一次调节量，多次自调节直至阶跃响应特征参数与理想模式吻合，完成自整定过程。文中方法无需预先对被控对象进行大量实验或仿真构建专家系统，只需确定理想模式的状态变量即可，具有适用性广的优点。

由增量式PI控制算法[9]可得出表达式：

（1）

式中 Δu为控制量的增量，在点焊控制器中为PWM输出占空比（PDC）的增量;Ig為恒压或恒流设定值;Is为焊接电压或电流的反馈采样值;下标k代表第k次控制周期。在阶跃响应的上升阶段，Ig>Isk>Isk-1 恒成立，因此，每在比较器环节执行比较后，若上升过快、最大超调过大，则自整定算法中应考虑减小ki或增大kp;反之，若上升时间过长、呈现过阻尼，则考虑增大ki或减小kp。

另外，由于PI算法为增量式，PDC需要一个初值pdc0，而当占空比小于一定值时，电源主电路IGBT导通时间很短，实际能产生的电流很微弱，且远远偏离使用范围。因此，若初始占空比pdc0不设为0，可缩短上升过程初期的时间，为了找到较合适的参数，需进行自整定。

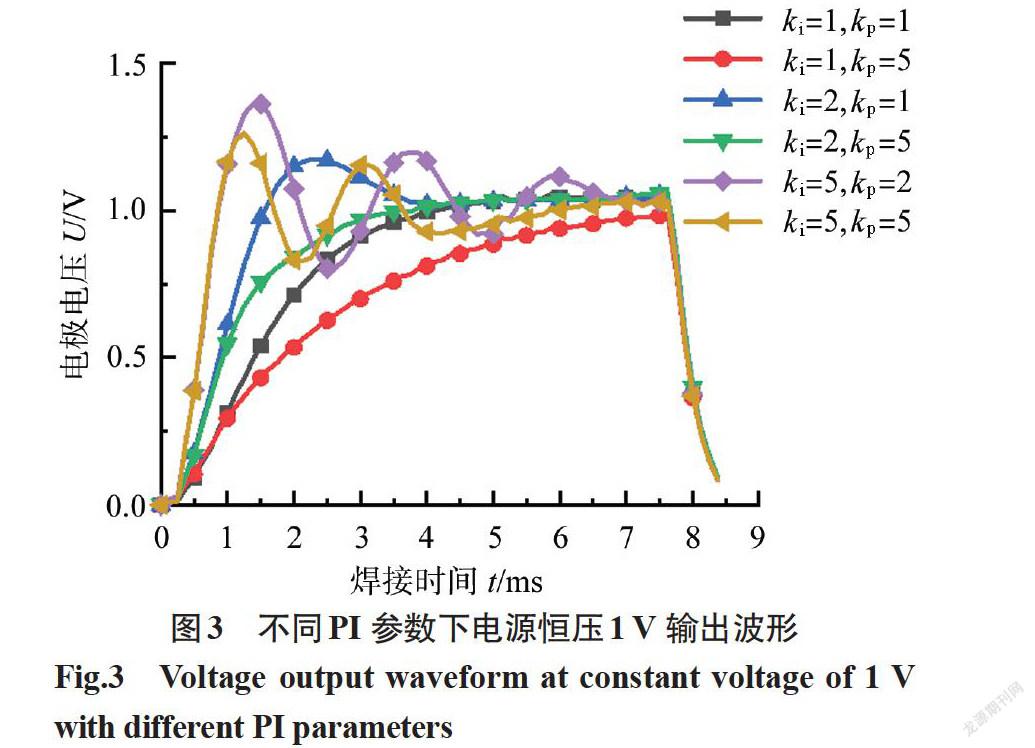
文中设计的点焊电源控制周期为0.25 ms，设定理想模式的阶跃响应指标为上升时间1.5～2.0 ms，即6～8个控制周期，且最大超调在2%以内。由式（1）及实验可知，在恒压放电这一阶跃响应初期Is值较小，比例环节累积的影响相对微弱，输出调节主要靠积分环节起作用，尤其在电源输出的前3个周期以内，在一定范围改变kp值对反馈得到的电压值影响微弱，如图 3所示。

因此，通过实验确定理想模式的阶跃响应曲线的第3周期电压反馈值u3与设定值U的比值α%（根据不同的阶跃响应指标，实际获得的α值不同，约在40～50之间）。自整定的第一步，按u3是否近似等于设定值U的α%调节积分系数ki。确定ki后，第二步是kp参数的自整定，以保证在目标上升时间8周期内使电压达到设定值U且没有明显超调。最后是pdc0的自整定，进一步缩短上升时间。

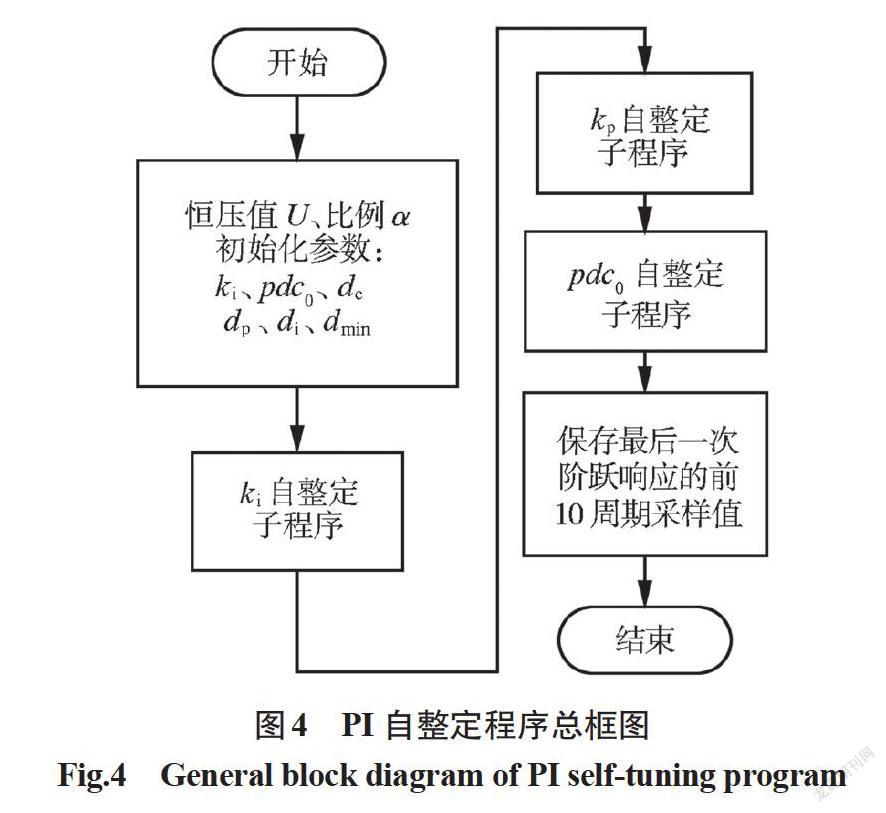
2 自整定程序流程

PI自整定程序框图如图 4所示。在3个自整定子程序开始之前，先确保在操作界面设定好恒压值U和比例α，程序先初始化PI参数ki及pdc0为一个较小的初值，并初始化ki、kp和pdc0对应的自调节步长di、dp和dc，及步长di、dp的下限dmin，注意此处所有值都为正数。由于初始占空比无需较高精度，故无需设置其步长下限。

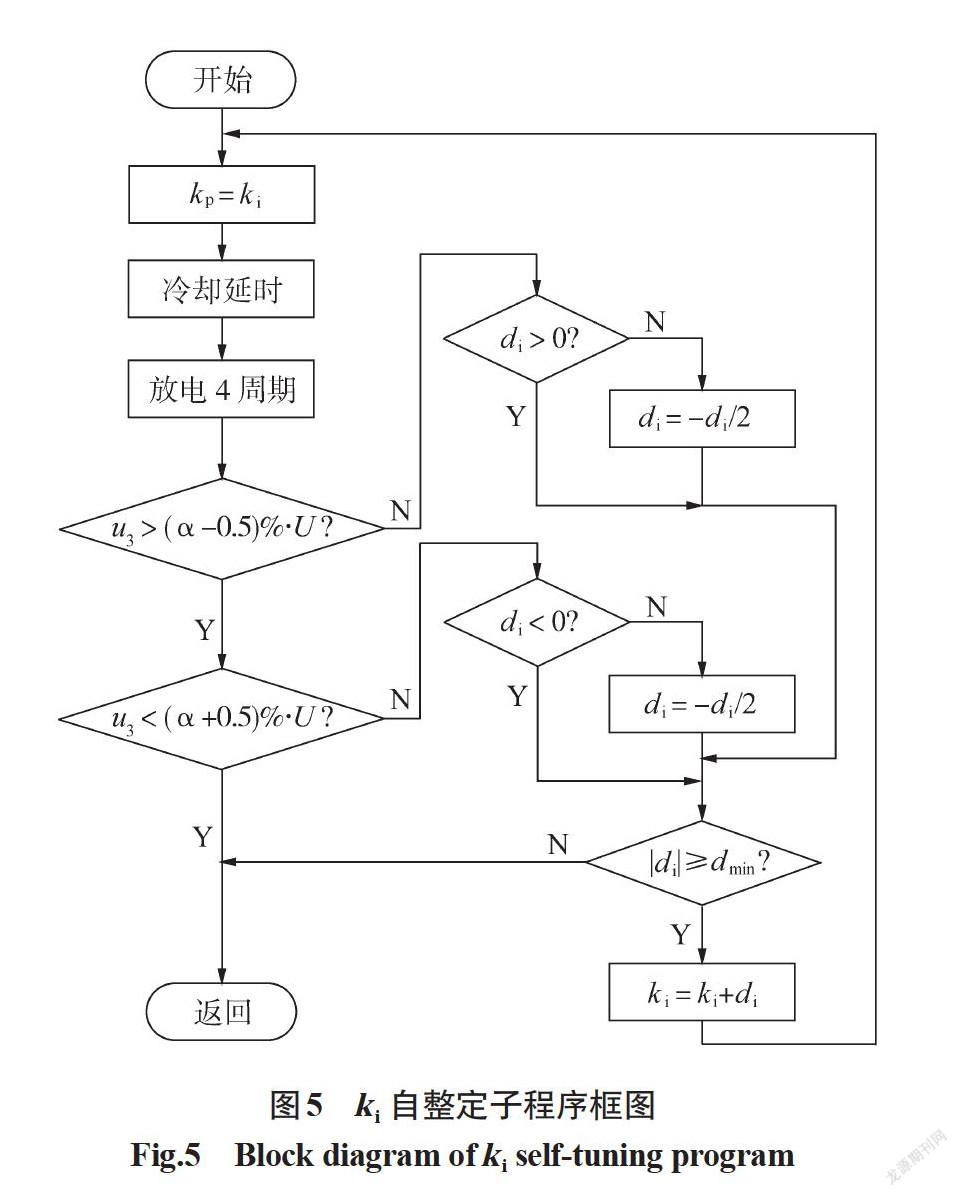
初始化完成后，进入ki自整定子程序，如图 5所示。刚进入子程序或每经ki参数自调节一次之后，都设定kp等于ki，在一定的冷却延时后，放电4周期（即1 ms）。其中，冷却延时的作用是确保每次放电前回路已无残余电流，且防止电极在自整定过程中过热或烧损。

此时，读取放电第3周期电压反馈值u3作为特征信息，并与设定值U的α%进行比较，分三种情况：（1）若两值近似相等，则结束子程序。 （2）若反馈值u3相对较小，则应增大ki，即本次步长di应为正;若上次di为正，则沿用，表明尚未锁定ki的区间，若上次di为负，则可锁定ki的区间，此处引入二分法思想，令di符号取反且值除以2。 （3）若u3相对较大，则应减小ki，即本次步长di应为负;若上次di为负，则沿用，表明尚未锁定ki的区间;若上次di为正，则可锁定ki的区间，令di符号取反且值除以2。

在比较环节结束后，判断本次计算后di绝对值是否小于最小步长dmin。若小于，则达到精度要求，结束子程序;否则，令ki加上步长di，完成一次调节并进入下一次调节过程。

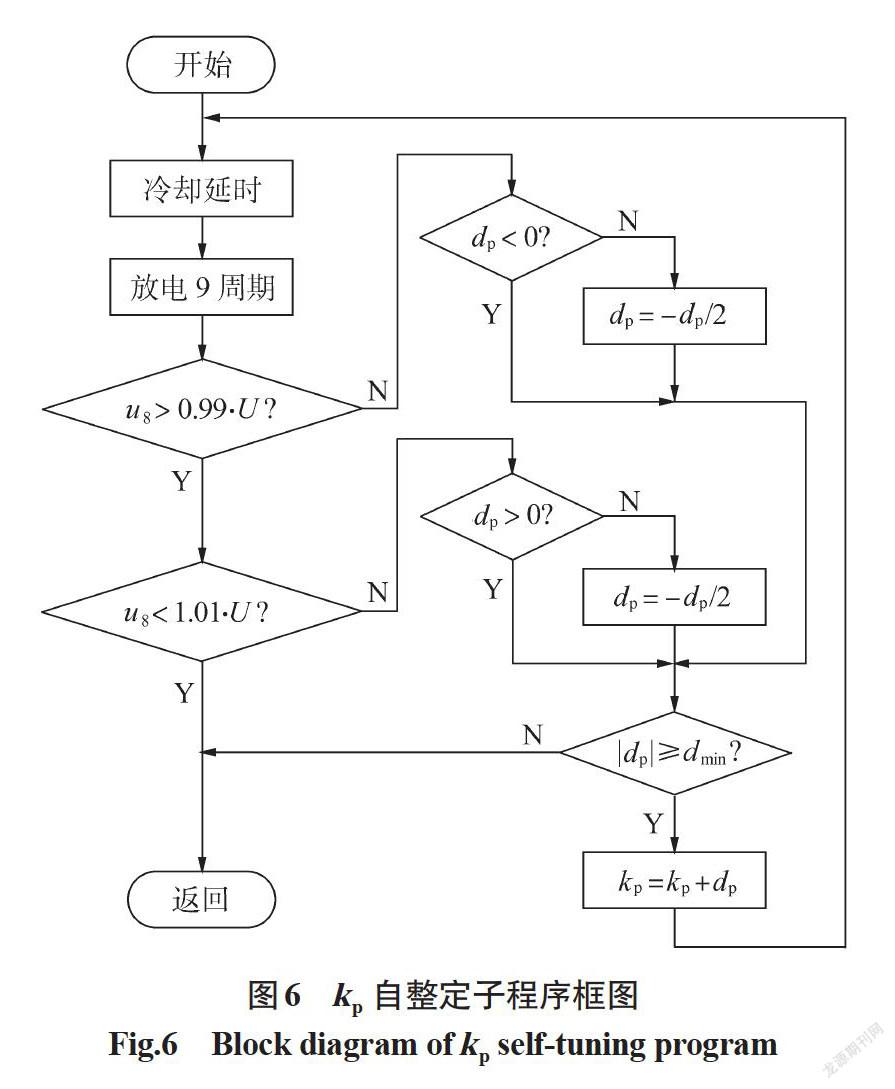
ki自整定完毕后进入kp自整定子程序，如图 6所示。kp与ki的自整定类似，只是识别的特征信息由第3周期电压反馈值u3变为第8周期电压反馈值u8，当u8与设定值U近似相等或步长dp绝对值小于最小步长dmin时，结束子程序。

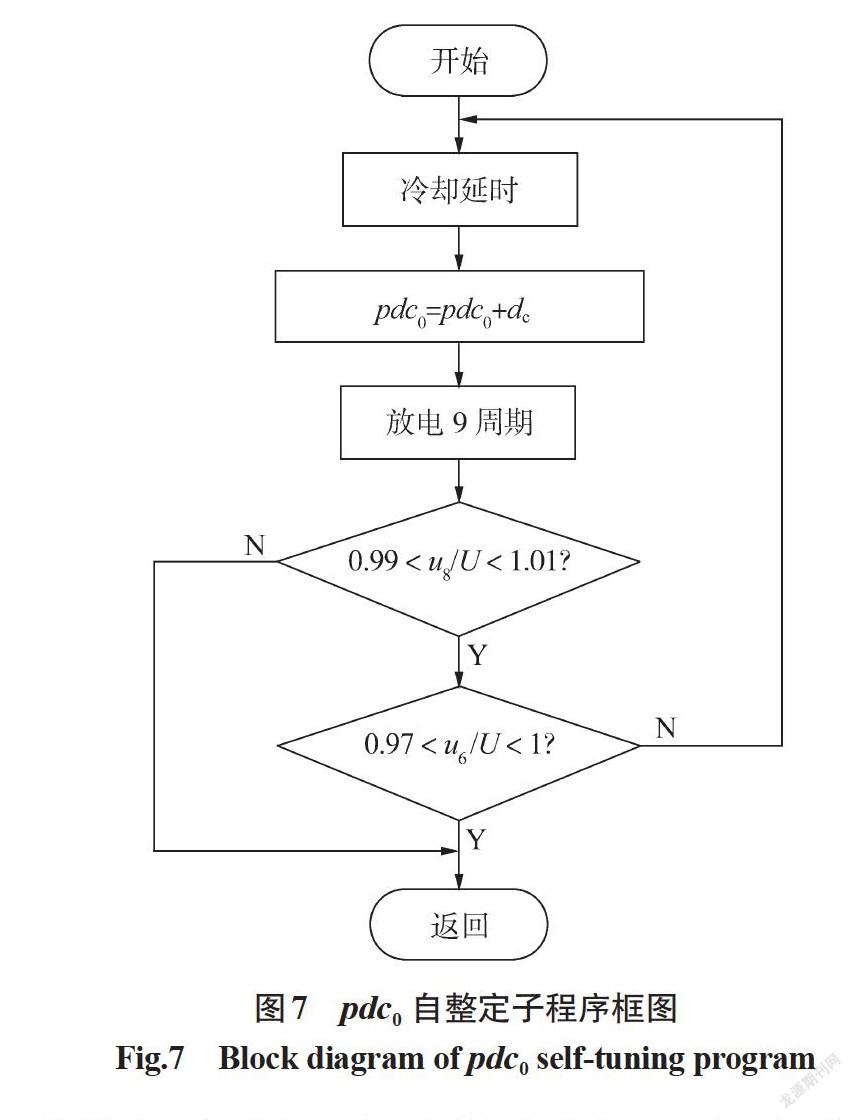
kp自整定完毕后进入pdc0自整定子程序，见图 7。与kp和ki相比较，pdc0无需较高精度，故无需二分迭代，此环节识别的特征信息是第8周期和第6周期的电压反馈值u8、u6，以进一步缩短上升时间。

三个参数的自调节次数之和一般在25次以内，由于一次调节过程时间很短，总时间不超过0.2 s，若自调节次数之和超过30次，会停止自整定并报警提示，以增强鲁棒性，防止电极过热烧损或其他异常。

3 实时监控策略

当三个参数都自整定结束后（见图 4），保存自整定过程中最后一次阶跃响应的前10周期电压采样值作为理想曲线，为后续焊接提供参考标准。将理想曲线上下平移一定值作为包络线，当后续焊接过程中的实时电压采样值超出包络曲线，电源会报警提示或自动执行PI参数自整定程序，以保证焊接过程的稳定性。

4 试验结果

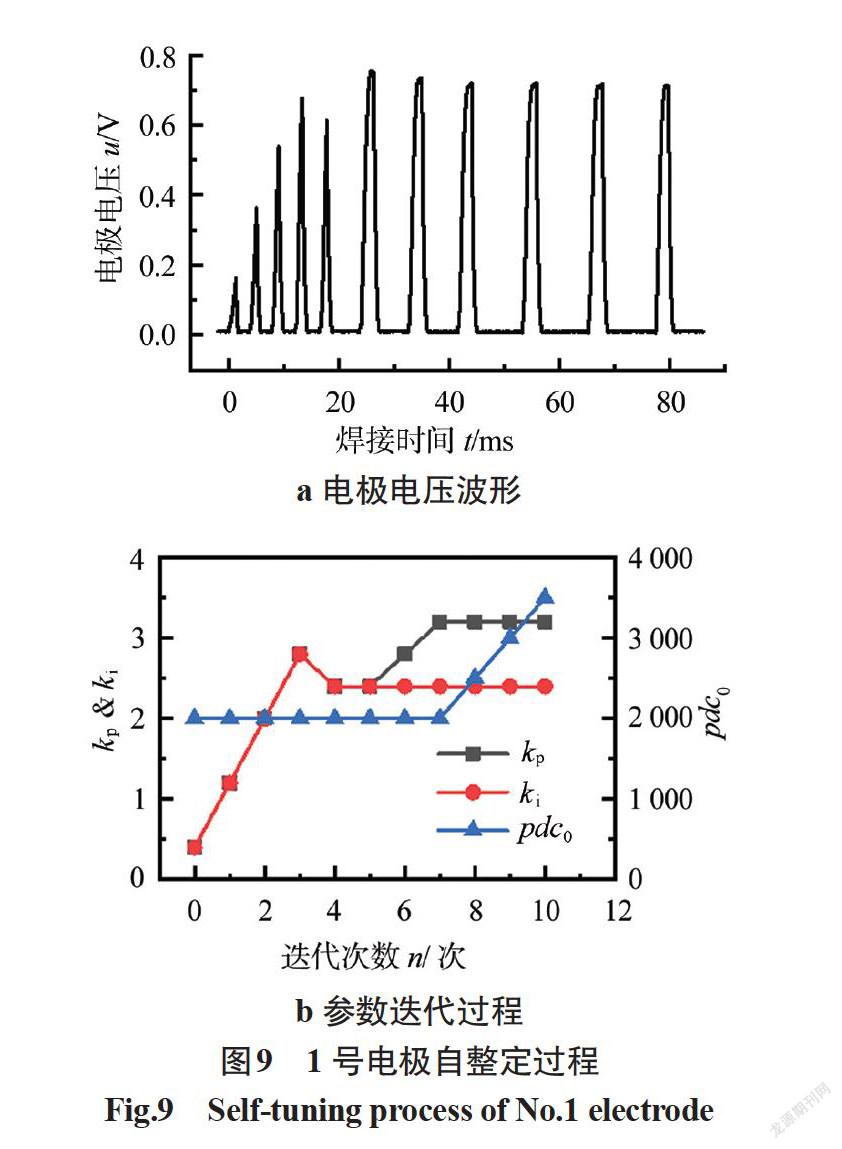
选取5种不同规格的针状漆包线点焊电极（见图 8），对电源进行PI自整定实验验证。点焊电源完整PWM周期为15 000时钟周期，恒压比例系数α为43，设定pdc0为2 000时钟周期，ki初值为0.4，di初值为0.8，dp初值为0.4，dmin为0.1，dc为500时钟周期。

以图中1号电极为例，设定恒压0.7 V，自整定全过程电极电压波形如图 9a所示，总耗时约80 ms。参数迭代过程如图 9b所示，ki自整定过程迭代4次，kp自整定过程迭代3次，pdc0自整定过程迭代3次，总迭代次数10次。1号电极自整定结束后，以恒压0.7 V进行漆包线点焊的电极电压波形如图 10所示，上升时间约为1.6 ms，最大超调在2%以内，符合预期标准。

经试验，5根电极参数自整定后均可在最大超调在2%以内的前提下将恒压输出的上升时间缩短至约1.6 ms。恒压0.7 V下自整定前后参数对比如表 1所示。由表1可知，在单一固定参数kp=ki=1时，恒压焊接的上升时间与电极电阻呈负相关，差异明显，且自整定后的kp、ki参数大小也大致与电极电阻呈负相关。

试验结果表明，为保证输出的一致性，漆包线点焊电极更换（或电极损耗导致电阻变化）后需要重新整定PI参数，且采用文中所述基于模式识别的PI自整定方法具有很好的整定效果。若某些点焊工艺需要较缓慢的上升过程，亦可额外自行设定匀速上升时间。

5 结论

（1）基于模式识别的PI自整定方法及实时监控策略计算简单，无需辨识过程模型及专家系统知识库，且二分法在保證精度的同时减少了自调节次数。在点焊恒压控制应用中自整定总时间不超过0.2 s，一般在更换电极或电极损耗较大时执行此功能。

（2）对点焊电源增加了PI自整定与实时监控功能后，提升了漆包线点焊过程的稳定性和响应的一致性，避免了人工调参过程，也更好地适应了短时间快速焊接的需要。

参考文献：

袁聪，郭钟宁，刘全军. 漆包线微连接技术综述[J]. 电加工与模具，2013（S1）：22-25，35.

杨仕桐，李远波，林健鸿. 脱漆焊——电阻焊焊接漆包线的新技术[J]. 焊接学报，2008（1）：21-25，114.

Binghua Mo，Zhongning Guo，Yuanbo Li，et al. Mechanism of Resistance Microwelding of Insulated Copper Wire to Phosphor Bronze Sheet[J]. MATERIALS TRANSACTIONS，2011，52（6）：1252-1258.

曾家铨，曹彪，杨凯，等. 漆包线电阻点焊电极烧损状态分析方法[J]. 华南理工大学学报（自然科学版），2019，47（12）：32-37.

吴敏，曹彪，杨凯，等. 不同控制模式下漆包线电极头的烧损规律[J]. 焊接，2019（3）：33-37.

穆克，苏成利. 一种改进的模式识别自整定PID控制方法[J]. 科学技术与工程，2012（7）：69-72.

周伟. PID参数自整定的研究与应用[D]. 湖北：华中科技大学，2011：22-23.

夏红，赏星耀，宋建成. PID参数自整定方法综述[J]. 浙江科技学院学报，2003（4）：236-240.

陶永华. 新型PID控制及其应用-第2版[M]. 北京：机械工业出版社，2002.