基于解析法的边坡稳定性分析程序设计及应用

王伟明

【摘   要】   针对公路或铁道工程中常用的4.5H法或36°线法确定圆弧滑动面的圆心具有一定偏差的问题，基于简化Bishop解析法，通过积分计算获得单一土层的直线型、折线型和階梯型路基安全稳定系数通用表达式。同时以MATLAB程序为平台编制可用于直线型、折线型和阶梯型路基的计算程序，并用4个算例检验程序的准确性。

【关键词】   公路路基;边坡稳定性程序;程序设计;路基边坡;简化Bishop法

Design and Application of Slope Stability Analysis Program

Based on Analytical Method

Wang Weiming

（Guangdong Construcion Polytechnic， Guangzhou 510440， China）

【Abstract】    In this paper， for the 4.5H method or 36° line method commonly used in highway or railway engineering， the center of the arc sliding surface has a certain deviation. Based on the simplified Bishop analytical method， the linear type， polyline type and ladder of a single soil layer are obtained through integral calculation General expression of type roadbed safety and stability coefficient. At the same time， the MATLAB program is used as the platform to compile the calculation program that can be used for straight line， broken line and stepped roadbed. Four examples are used to verify the accuracy of the program.

【Key words】     highway roadbed; slope stability program; program design; subgrade slope; simplified Bishop method

〔中图分类号〕  U416.1    〔文献标识码〕  A              〔文章编号〕 1674 - 3229（2021）01- 0075 - 04

0     引言

目前我国公路或铁道工程建设中，黏性土的路基边坡稳定性通常采用简化Bishop法进行分析，先以4.5H法或36°线法确定圆弧滑动面的圆心位置，再通过迭代计算获得稳定系数。该方法最大的问题在于通常不能精确确定最危险滑动圆弧圆心位置，有时会出现稳定系数偏差较大的情况，从而影响稳定性的判断。

国内基于C语言、Visual Basic、MATLAB程序出现了不少边坡稳定性的计算程序[1-2]，但这些程序大都以求解直线型边坡为主。本文基于简化Bishop解析法[3-6]，以MATLAB程序为平台编制可用于直线型、折线型和阶梯型路基的计算程序。

1     圆弧条分法的解析表达式

简化Bishop法由于考虑土条间的相互作用，因此其精度较高，也是现行规范的推荐方法之一，但在计算过程中需对划分的每一条块一一求和，计算过程繁杂，且容易出错。而通过积分法既可简化过程又可提高计算精度。

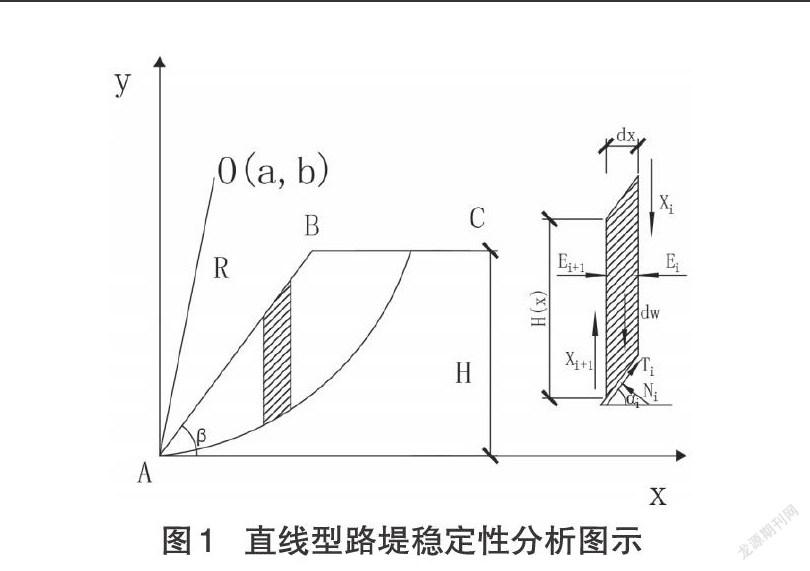
简约Bishop法的稳定性系数公式为隐式解，可通过积分的方法获得其显式的解析表达式，其中以直线型路堤为例，一般情况下滑动面过坡脚，以坡脚为原点，受力分析图示见图1。

本文参考文献[4]的解析计算，其稳定安全系数见公式（1）。

[FS=10lrh（x）sinadx0lc+rh（x）tanϕcosα+tanϕFSsinαdx] （1）

[h（x）=xtanβ-（b-R2-（x-a）2）（0≤x≤Hcotβ）H-（b-R2-（x-a）2）（Hcotβ≤x≤a+R2-（H-b）2）] （2）

公式（1）中，[c]为土的粘聚力，[γ]为土的重度，[ϕ]为土的内摩擦角，（a，b）为圆心坐标，[l=a+R2-（H-b）2]，[sinα=x-aR]，[cosα=R2-（x-a）2R]，R为圆弧半径，土条间竖向剪力Xi，Xi+1忽略不计。

折线型和阶梯型路堤的计算公式与之类似，主要是[h（x）]函数有区别，见公式（3）（4）。

[h（x）=xtanβ1-（b-R2-（x-a）2）（0≤x≤H1cotβ1）H1+（x-H1cotβ1）tanβ2-（b-R2-（x-a）2）（H1cotβ1≤x≤H1cotβ1+H2cotβ2）H-（b-R2-（x-a）2）（H1cotβ1+H2cotβ2≤x≤a+R2-（H-b）2）] （3）

[h（x）=xtanβ1-（b-R2-（x-a）2）（0≤x≤H1cotβ1）H1-（b-R2-（x-a）2）（H1cotβ1≤x≤H1cotβ1+b1）H1+（x-H1cotβ1-b1）tanβ2-（b-R2-（x-a）2）（H1cotβ1+b1≤x≤H1cotβ1+H2cotβ2+b1）H-（b-R2-（x-a）2）（H1cotβ1+H2cotβ2+b1≤x≤a+R2-（H-b）2）]（4）

公式（3）中，[H1]、[H2]分别为折线段高度，[β1]、[β2]为相应折线段角度，这里只列举两条折线的[h（x）]函数，如有多段可以此类推。

公式（4）中的b1为阶梯型路堤平台宽度，其他符号含义如前所述，如有几个台阶亦可以此类推。

依据以上几式，由公式（1）通过积分计算可获得单一土层的直线型、折线型和阶梯型路基安全稳定系数，通用表达式见公式（5），式中的积分可通过MATLAB程序求解。

[FS=1IW[c/rIc（FS）+tanϕH（FS）]] （5）

其中[IW=0a+R2-（H-b）2h（x）sinαdx];

[IC（FS）=0a+R2-（H-b）2dxcosα+tanϕ/FSsinα];

[H（FS）=0a+R2-（H-b）2h（x）dxcosα+tanϕ/FSsinα]，[h（x）]见公式（2）-（4）。

如遇不同填土组合，则应以公式（1）为基础，考虑土层分布，依据土层[r]、[c]、[tanϕ]的值灵活调整积分区间分多段积分，积分后获得表达式。

2     程序编制思路

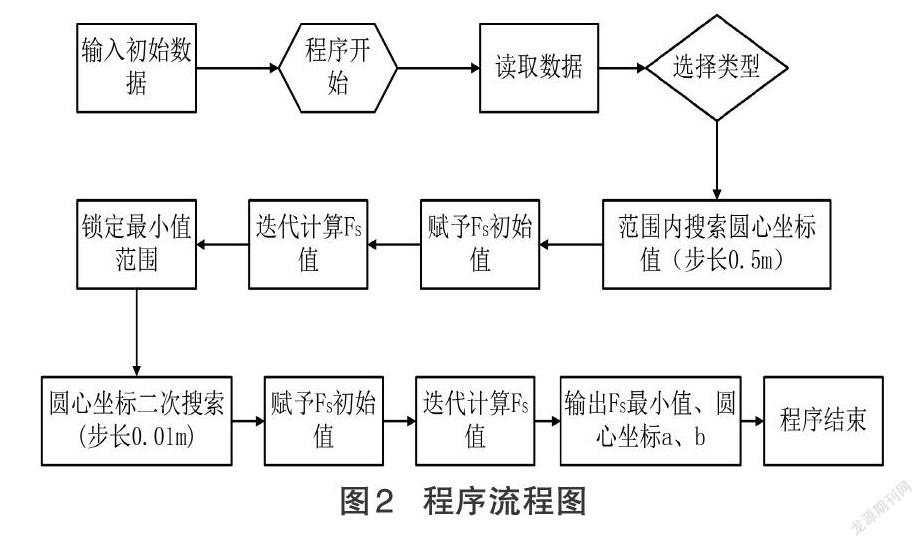
根据[FS]的表达式可知，每一滑动面都对应一个稳定安全系数值，求取稳定安全系数最小值的本质也即寻找最危险滑动面的圆心坐标。依据文献[1]的试算，圆心坐标的取值范围为[-2H≤a≤Hcotϕ]，[H≤b≤3H]。本文对上述圆心坐标范围进行搜索，为加快程序计算速度同时考虑强精度，初始搜索步长为0.5m，先给[FS]一初始值，依据公式（5）迭代计算[FS]，依据[FS]最小值初步锁定危险圆弧滑动面的圆心坐标坐标范围，以步长0.01m进行再次搜索并迭代计算，最终锁定最危险滑动面的圆心坐标，输出[FS]值，这样既减少程序迭代计算时间又保证了精度。

根据以上思路编制了计算程序，其流程图见图2。

3     可靠性检验与应用

3.1   程序可靠性检验

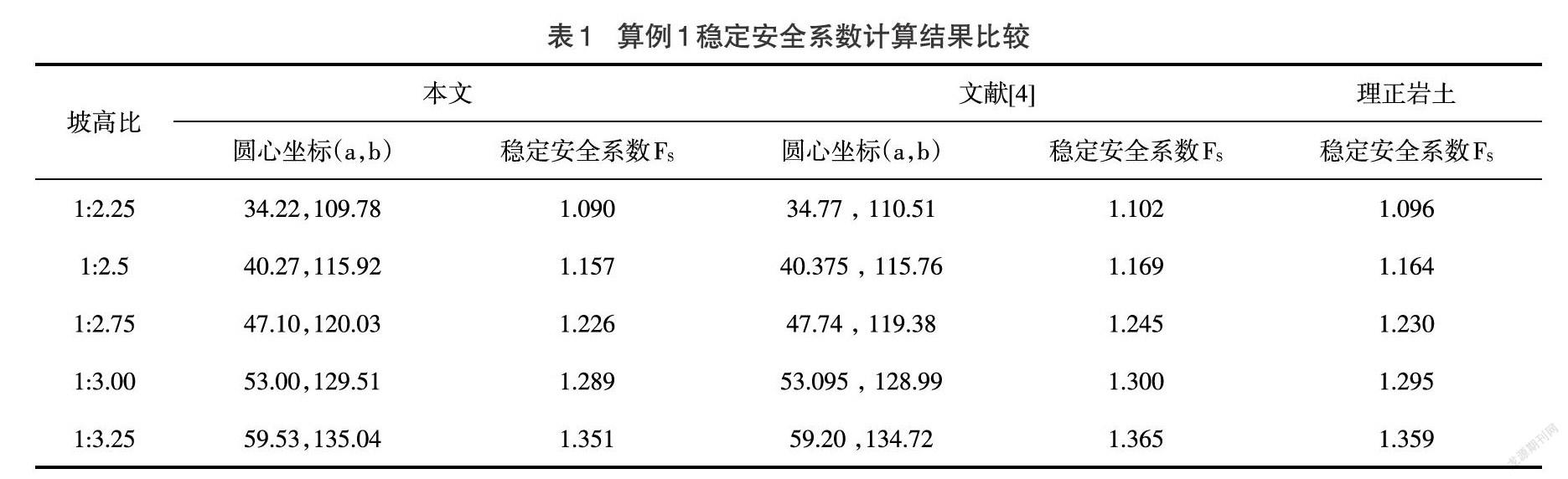
算例1：文献[4]引用文献[8]的算例作为可靠性检验，本文同样应用该算例。条件为土的重度[γ=19.62kN/m3]、粘聚力[c=58.86kPa]、摩擦系数[tanϕ=0.2]，边坡高度[H=50m]，坡高比为[1：2.25]、[1：2.5]、[1：2.75]、[1：3]、[1：3.25]，同时以工程中常用的理正岩土软件（6.5版）选择简化 Bishop条分法进行建模计算，结果见表1。

由表1数据可知，本文的计算结果较文献[4]偏小1%～1.5%，较理正岩土计算结果偏小0.3%～0.6%，总体而言误差较小，不影响结果判断。另外本文计算程序每一圆心坐标下的迭代次数为2～3次，即可获得满足精度要求的[FS]值。本文与文献[4]的误差可能源于程序计算与手算之间的精度误差。

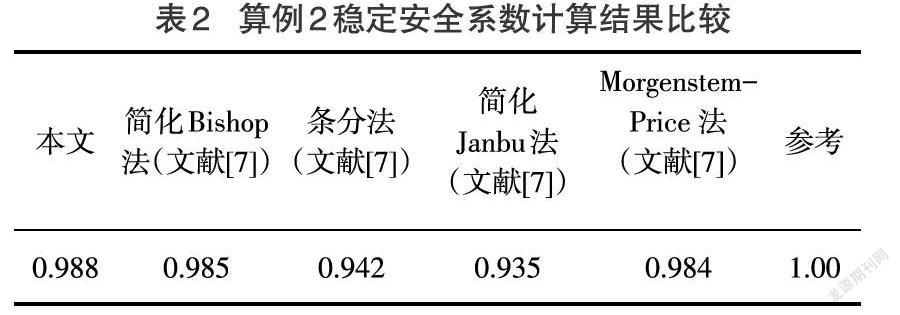
算例2：以文獻[7]的算例1作为本文的算例2。条件为土的重度[γ=20kN/m3]、粘聚力[c=3kPa]、内摩擦角[ϕ=19.6°]，边坡高度[H=10m]，坡高比为[1：2]，计算结果见表2。

算例2为澳大利亚计算机应用协会（ACADS）针对边坡稳定性计算程序而设计的考核题之一EX11，本题的参考答案为1.00。

由表2 的数据可知本文的计算程序与文献[7]中所有方法的计算结果都接近参考答案，这表明本文直线型边坡计算程序具有准确性。

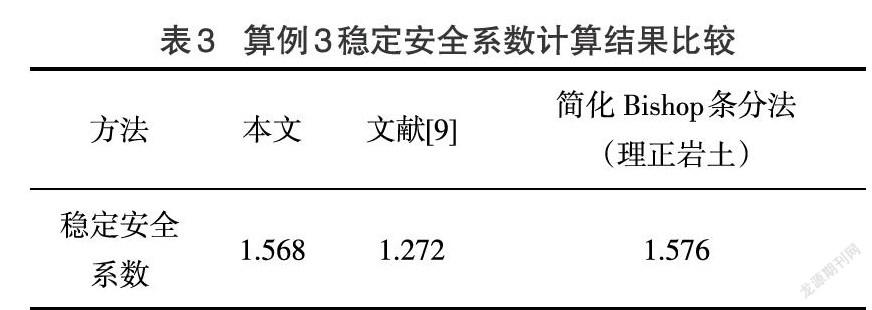
算例3：以文献[9]的比较算例作为本文的算例3。某高路堤，填土容重[γ=13.2kN/m3]，粘聚力[c=42.5kPa]、内摩擦角[ϕ=15°]、边坡高度[H=25m]，其中路基顶面以下8m坡高比为1：1.5，8m以下为1：1.75，荷载换算土高度为1m，计算结果见表3。

本文计算程序的计算结果较理正岩土计算值偏小0.51%，在工程实践中偏于保守，具有一定的实际意义，这也表明本文折线型边坡计算的准确性。而文献[9]的计算结果与本文及理正岩土相差较大，原因可能是因为其采用的是4.5H法确定圆心，结果存在一定的偏差。

算例4：某地路堑边坡，填土容重[γ=18kN/m3]，粘聚力[c=25kPa]、内摩擦角[ϕ=23°]、边坡高度[H=20m]，路基顶面以下8m坡高比为1：1.5，8m以下为1：1.75，中间平台宽度2m。

计算结果：本文为1.583，理正岩土（简化 Bishop条分法）为1.593。本文计算程序的计算结果较理正岩土计算值偏小0.63%，两者误差较小，表明本文阶梯型边坡计算程序的准确性可得到保证。

综合以上4个算例，说明本文计算程序计算结果可靠，对工程实践具有一定的指导意义。

3.2   应用

某路堤边坡高度为25m，填土容重[γ=17.4kN/m3，]

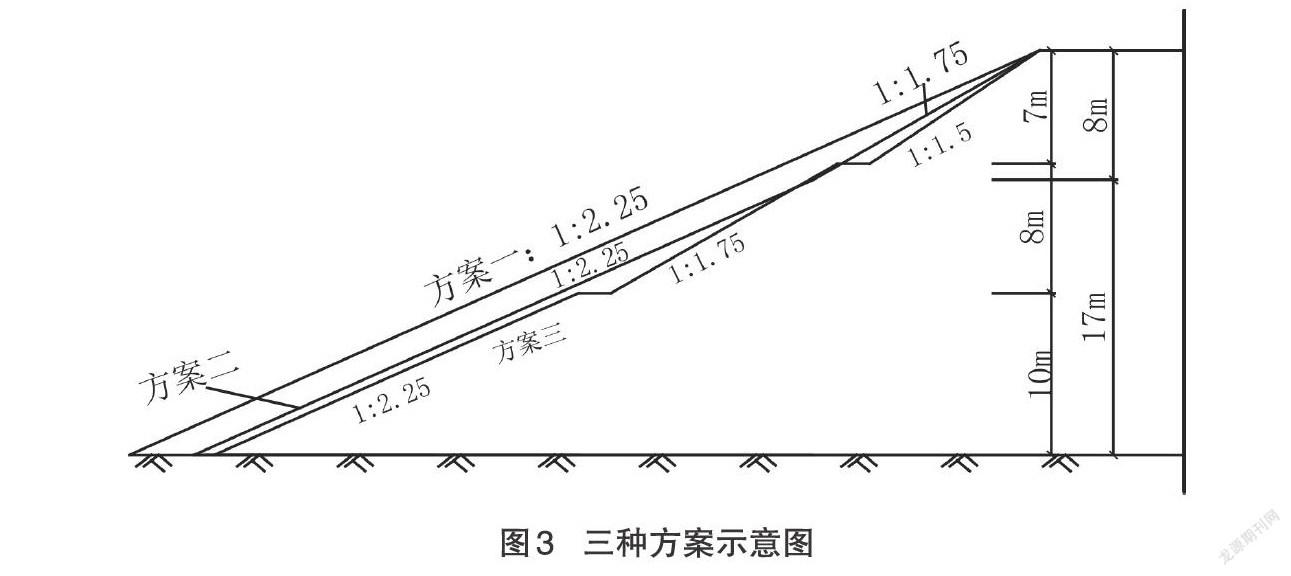
粘聚力[c=20kPa]、内摩擦角[ϕ=20°]，有3个方案可供选择，方案一直线型边坡;方案二折线型边坡;方案三阶梯型边坡。经本文软件计算，以FS≥1.35为目标，完成3个方案设计，结果见表4和图3。

由表4可知，以上3个方案均满足FS>1.35，稳定性满足要求。从图3可知，方案三在满足稳定性要求的前提下比较经济，且坡度较平缓，可缓和雨水对边坡的冲刷。综合考虑各项技术经济指标，选择方案三。

4     结论

本文编制的MATLAB计算程序可用于直线型、折线型和阶梯型路基的稳定安全系数计算，与国内其他计算方法的误差较小，三类路基的计算结果与工程中常用的理正岩土软件误差在0.3%～0.6%之间，精度可满足工程需求，可用于工程实践，具有一定的实用价值。本文程序目前尚不能对复杂土层进行稳定性分析，这也是今后的努力方向。

[参考文献]

[1] 李明.边坡最危险滑动圆弧圆心位置的程序搜索及其应用[J].南华大学学报（自然科学版），2004，18（4）：63-66.

[2] 王娅娟.基于Matlab软件的边坡结构可靠度程序设计及应用研究[D].呼和浩特：内蒙古工业大学，2018.

[3] 卢玉林，薄景山，陈晓冉，等.瑞典圆弧法积分模型的边坡稳定性解析计算[J].应用力学学报，2017，34（2）：257-263.

[4] 蒋斌松，康伟.边坡稳定性中BISHOP 法的解析计算[J].中国矿业大学学报，2008，37（3）：287-290.

[5] 蒋斌松，蔡美峰，吕爱钟.边坡稳定性的解析计算[J].岩石力学与工程学报，2004，23（16）：2726-2729.

[6] 杨庚宇，赵少飞.土坡稳定分析圆弧滑动法的解析解[A].第七届全国结构工程学术会议论文集（第Ⅱ卷）[C].1998.

[7] 邓东平，李 亮.两种滑动面型式下边坡稳定性计算方法的研究[J].岩土力学，2013，34（2）：372-380.

[8] 张天宝.土坡稳定分析和土工建筑物的边坡设计[M].成都：成都科技大学出版社， 1987： 20.

[9] 彭波.青岛至兰州公路（宁夏境）东山坡至毛家沟段高速公路路基边坡稳定性研究[D].西安：长安大学，2011.