数学教学中的“眼、脑、手”并用
2021-09-10肖心知
肖心知

中图分类号:A 文献标识码:A 文章编号:(2021)-14-380
人教版初中《数学》教学大綱,强调教师在数学教学中,应全方位激发学生的学习积极性,充分提供从事数学教学的机会,帮助他们在自主探索和合作交流的过程中,真正理解和掌握基本的数学知识与技能、数学思想与数学方法,获得广泛的数学活动经验,从而让学生掌握数学知识,同时在思想能力、情感态度与价值观等多方面得到进一步的发展。
那怎么才能做到这一点呢?笔者做了一番尝试。
一、数学现象的了解、结论的得出,学生离不开观察——“动眼”
所谓“动眼”,就是指学生在学习数学知识时,应选取有现实意义的富有挑战性的数学内容,让学生进行用眼观察。通过观察理解数学知识,强化数学观点,提高运用数学知识的能力。
当我们教《位置的确定》时,教师应先结合学生自身的位置,找好观察点,再用眼进行观察,学生才会判断物体的位置。
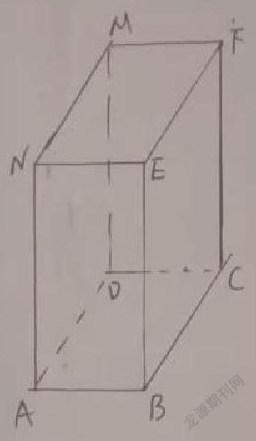
人教版七年级上册数学第117页探究题:如右图所示,是一个由9个正方体组成的立方体图形,分别从正面、左面、上面观察这个图形,各能得到怎样的平面图形?
在让学生回答这个问题时,教师可以先让学生用小正方体摆放出这个模型,在让学生用眼从正面、左面、上面仔细观察这个模型,才能得到各视面的平面图形。
二、数学知识的理解、原理的运用,学生也离不开思考——“动脑”
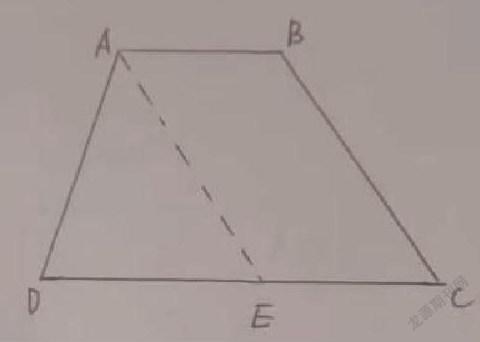
如图,已知梯形ABCD中,AB//CD、∠C=50 o、∠D=80 o、 AB=2厘米、CD=9厘米,求AD的长。
我们想:若将线段AB平移到EC, 得EC=AB,从而DE=DC-EC=DC-AB=9-2=7(厘米)
又可得∠AED=∠C=50 o
∴∠DAE=180 o-∠D-∠AED =50 o
∴∠AED =∠DAE
AD=DE=7(厘米)
学生通过仔细思考,大胆想象,借助平移,就构造出等腰△DAE,从而得出AD=DE=7厘米.
动脑思考,能让学生掌握数学知识,理解数学原理,教师既应将其放在教学首位,也应贯穿教学始终。
三、数学知识的获取、思想的领悟,学生还离不开操作——“动手”
新教学理念强调学生动手实验,从实贱中获取知识。
动手能让人亲身体验,切身感受数学知识的形成过程。
在教“正方形是特殊的棱形”这一知识点时,让学生做一个棱形学具(顶点处可活动),当满足菱形有一个内角为90°时,这时四边形会变成为正方形。
通过这样的操作实验,学生在头脑形成这一数学知识,强化了“有一个角是直角的菱形就是正方形”的概念。
四、数学原理的揭示,技能的提高,学生更离不开“眼、脑、手”合用
“眼、脑、手”并用,首先是观察数学现象,形成表象,再思考某些数学原理。但动手操作,亲身实验是验证数学现象的真伪、加深理解数学原理的重要环节。
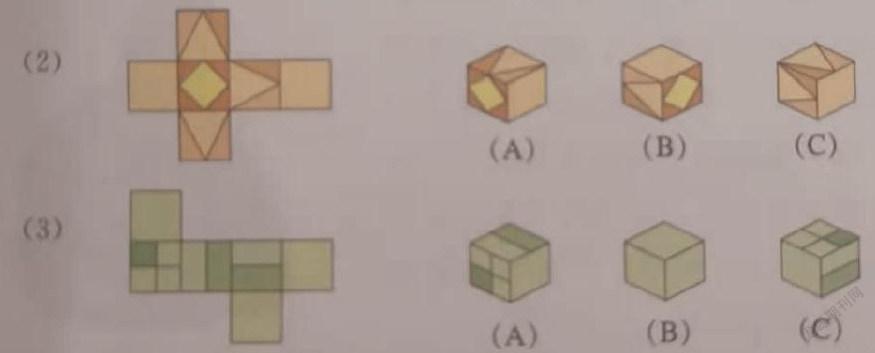
如:人教版数学七年级上第123页的13(2)(3)题:
如上图,左边的图形可能是右边哪些图形的展开图?
这个问题学生难回答。
我们不仿先动手(操作)剪成(2)(3)左边的平面图,描成彩图,再折成正(长)方体;在观察哪个图形是符合折成正(长)方体,接着又让学生观察,再思考,到底选取哪个答案。只有这样让学生动手操作、用眼观察、用脑思考才能很快的获取数学知识,了解数学原理,提高数学技能。
数学知识的获取,数学能力的培养,离不开动“眼、脑、手”。
实践证明,数学课堂引导学生“眼、脑、手”并用,能够有效激发他们积极参与教学活动,观察数学现象,获得数学经验,学会数学知识,感悟数学原理,领悟数学思想,揭示数学本质,提高数学技能,享受数学人生。
湖北洪湖市滨湖办事处中心学校
