快递物流网络与配送中心布局优化研究

胥文 张冰洁

摘 要：快递物流网络和配送中心的合理布局与快递企业的总体成本和服务水平直接相关，合理科学的布局对于快递企业的配送效率和运营效益具有重要的作用。本文针对快递企业二级网络配送中心优化问题，考虑包括建设成本、人工成本、上下游运输成本等多项成本，构建以布局总成本最小为目标函数的快递企业二级配送中心布局优化模型，并采用了一种新的启发式算法即复合型交叉进化算法（SCE-UA）来解决二级配送中心布局优化模型的求解问题。以瀘州市某快递公司为例，综合考虑各点的业务数量和成本，研究结果表明该算法能够高效、快速地收敛到全局最优解，可有效优化减少配送点数量，在布局总成本和各单项成本可降低5%～15%，算法多次迭代下误差低于2%，具有较好稳定性。

关键词：物流网络;配送中心;SCE-UA模型;布局优化

1 绪论

快递企业各层级网络配送中心的数量及分布直接关系到快递企业的总体成本和服务水平，布局现状是否合理、科学，其在快递网络中的地位和作用是否适当，是快递企业迫切需要改善和优化的重要问题。二级配送中心作为物流网络中承上启下重要的一环，其布局优化模型是一个大规模的非线性优化问题，采用精确算法常常无法取得满意解[1-2]，复合型交叉进化算法（Shuffled Complex Evolution，缩写为SCE-UA）是一种全局优化算法，最早由美国亚利桑那州大学Duan等人提出，它是一种能很好解决非线性约束最优化问题的进化算法[3]，具有较强的全局搜索能力[4]。模型参数优化的问题中，部分研究通过对遗传算法、随机算法、SCE-UA算法的效率进行了对比，表明SCE-UA算法在三种算法中收敛效果最佳[5]，算法鲁棒性较好[6]，能够较好的运用于最优化模型优化问题[7-8]，同时在求解最小值问题模型的求解中有较好的效果[9-10]。从算法的应用难度来看，SCE-UA算法的参数虽然较多，但大部分的取值都可以沿用已有研究成果的默认值，只有复合型个数v需要根据具体问题具体确定，因此应用起来难度不是很大。从算法的求解效率来看，SCE-UA综合了确定性搜索、随机搜索和生物竞争进化等方法的优点，引入种群概念，具有很强的收敛性和运算效率，具备较好的解决物流网络网点布局优化非线性优化问题求解潜力。

2 模型构建

2.1 模型建立

本文构建以布局总成本最小为目标函数的快递企业二级配送中心布局优化模型，考虑包括建设成本、人工成本、上下游运输成本等多项成本。在考虑下游运输问题时，针对快递配送的时效性，结合配送车辆路径优化的相关理论，对向下游各快递取送点的配送顺序和路线问题进行优化，研究的问题主要定义为多个二级配送中心、单次配送、若干个快递取送点、带有时间窗的快递配送车辆路径优化问题，快递车辆从多个二级配送中心出发对若干个快递取送点进行配送服务。在配送过程中，要求每辆车只能从一个二级配送中心出发，完成配送工作后必须返回到这个相同的二级配送中心。已知二级配送中心和各快递取送点位置、各取送点的需求、车辆的最大载重量，要求合理安排车辆配送路线和行车顺序，使目标函数得到最优，并利用 SCE-UA算法进行求解，该算法结合了遗传算法和单纯形法的优点，能够高效、快速地收敛到全局最优解。相应的数学模型构建如下列公式所示。

V：车队规模，即车辆的总数目;V：车辆编号;N：有待配送的取送点的总数目;i，j：取送点编号;：取送点i与j之间线路上的单位运输成本;：取送点i与j之间的距离;：取送点i需要配送的快递数量;：配送车辆v分别到达取送点i和取送点3的时点;：车辆在取送点i，j之间的行驶时间。

2.2 SCE-UA算法求解

采用SCE-UA算法求解此模型的基本步骤如下，算法流程如图1所示。（1）初始化：对参与进化的复合形的个数v以及每个复合形所包含的样本数目m进行初始化，样本点数目为s =vm;（2）产生样本：在可行域内随机产生s个样本点;（3）排序标号：计算样本的函数值，并将其排序标号;（4）构造复合形：将s个样本划分成v个包含m个点的复合形;（5）复合形进化：通过初始化构造子复合形，进行反射和收缩;（6）复合形掺混：将所有进化后的复合形中的点重新合并，组成一个新的样本集合;（7） 收敛性判断：如果满足收敛条件则停止。

3 案例分析

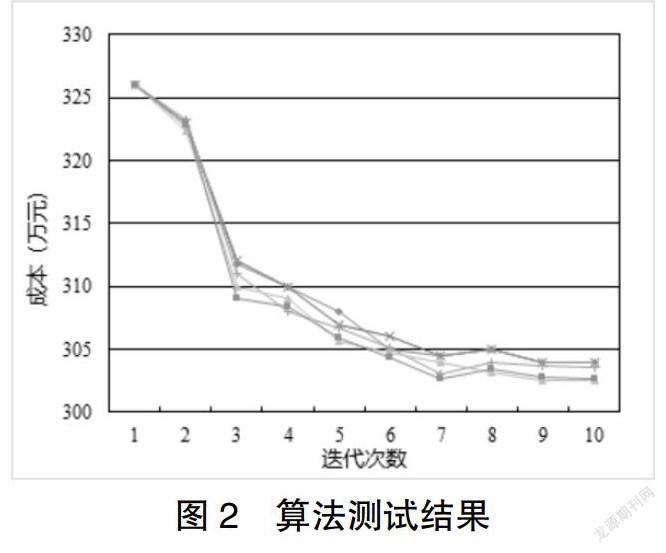
本文选定泸州市某快递公司进行实例分析，结合实地调研得到的某快递公司在泸州区范围内各级配送中心的布局现状及相关数据，旨在通过对实例结果的对比分析验证本文提出的二级配送中心布局优化模型的有效性。某物流公司在泸州市的布局现状是：一级配送中心1个，二级配送中心36个，每个二级配送中心负责范围内的快递取送点数量为几十个不等。以泸州市区社区为单位，可以统计出各二级配送中心负责区域内的家庭数量H，其中，每个二级配送中心平均家庭数量20 983，最高家庭数量33 278，最低数量为8 976，假设平均每个家庭的快递持有量为P件/天，因此通过公式Q=H*P我们就可以计算出各二级配送中心每天需处理的快递件总量。各参数取值为平日1 500件/天，周末800件/天，额外路径费用0.1元/件，运费0.49元/公里，额外运费0.2元/公里。SCE-UA算法的参数虽然较多，但绝大部分的取值都可以采用已有研究成果的默认值，只有复合型个数v需要根据具体问题确定，根据文献[11]，SCE-UA算法的参数最优取值相互关系为m=19，v=2，z=10，λ=1，ε=19。经过算法优化之后，二级配送中心的数量由之前的36个减少到33个，为了对优化的结果进行检验，本文将二级配送中心布局优化前后的各项成本和总成本都进行了比较，本文设计的模型并不是考虑每个二级配送中心成本费用的高低，而是使布局总成本最低。根据对优化前后布局的结果进行比较，我们得出，经过优化布局总成本由3 269 072减少到3 018 834，降低了7.7%。其中建设成本由603 241减少到507 246，降低了14.7%;人工成本由1 510 600减少到1 414 600，降低5.9%;上游运输成本由330 666减少到300 198，降低了8.9%;下游运输成本由724 565减少到686 790，降低了5.2%。经过优化之后的结果无论是从布局总成本还是各单项成本来看，均有所下降，从而验证了本文模型和算法在快递企业二级配送中心布局优化问题方面具有一定的有效性和可行性。最后，为了检验本文提出的算法的效率，我们是在相同的参数下进行测试，测试结果如图2 所示，在大约迭代到10次试算，每次试算迭代到7次左右，算法趋向于收敛，此外，7次试算结果最大相差不超过2%，说明算法的稳定性较好。

4 结论

本文构建以布局总成本最小为目标，构建快递企业二级配送中心布局优化模型，考虑包括建设成本、人工成本、上下游运输成本等多项成本，构建了物流网络非线性模型，并选定泸州市某快递公司為例，采用模型和SCE-UA算法进行具体求解，对比优化前后布局的结果，无论是布局总成本还是各单项成本，优化降低5%～15%了成本，在保持效益不变下，有效减少了配送中心数量。同时在相同参数测试7次迭代下表明，误差均低于2%，算法适用性较好。

参考文献：

[1]Hapuarachchi H A，Wang S H.Application of SCE-UA method for calibrating the Xinanjiang watershed model，Journal of Lake Science，2001，12（4）：304-314.

[2]马海波.SCE-UA算法在TOP-MODEL参数优化中的应用[J].河海大学学报，2006（3）：361-364.

[3]Duan Q，Gupta V K，Sorooshian S.Shuffled complex evolution approach for effective and efficient global minimization[J].Journal of Optimization Theory and Applications，1993，76（3）：501-521.

[4]宋星原.SCE-UA、遗传算法和单纯形优化算法的应用[J].武汉大学学报，2009（42）：1.

[5]Kuczera G.Efficient subspace probabilistic parameter optimization for catchment models.Water Resources Research，1997，33（1）：177-185.

[6]Sorooshian S，Duan Q Y，Gupta V K.Optimal use of the SCE-UA g lobal optimization method for calibrating watershed models[J].Journal of Hydrology，1994，158（3-4）：265-284.

[7]陈宝林.最优化理论与算法[M].北京：清华大学出版社，2005：411-419.

[8]Nelder J A，Mead R I.A simplex method for function minimization[J].Computer Journal，1965，7（4）：308-313.

[9]于滨.公交线路发车频率优化的双层规划模型及其解法[J].吉林大学学报，2006（36）：5.

[10]王道平，徐展，杨岑.基于两阶段启发式算法的物流配送选址-路径问题研究[J].运筹与管理，2017，26（4）：70-75.

[11]郭生练，闰宝伟，肖义，等.Copula函数在多变量水文分析计算中的应用及研究进展[J].水文，2008，28（3）：1-7.