关注问题探究，促进学生学习

张超

中图分类号：G4 文献标识码：A 文章编号：（2021）-2-169

认知心理学认为：学生学习的过程是一个把教材知识结构转化为自己认知结构的过程。”高效的解题练习有助于学生认知结构的过程。学生学习能力的提升，大多通过数学解题训练获得，如何在课堂中高效的开展探究性学习，怎样能够让学生通过对解题的反思获得“关键能力”，引发了笔者的思考，现将自己教学过程中的一些想法，供给大家指正。

问题呈现 如图1：△ABC中，AD是角平分线，∠B=2∠C.求证：AC=AB+BD.

对于探究线段和差关系，解题思路往往是通过“截长补短”构造三角形全等，利用图形全等进行线段的转化。

解法1（截长）图2中，在AC边截取线段AE=AB，连接DE，根据AE=AB，AD是∠BAE的角平分线，AD公共边三个条件，判定△ABD≌△AED。从而AB转化为AE，再由∠B=∠AED=2∠C，得到ED=EC=BD，即AC=AB+BD。

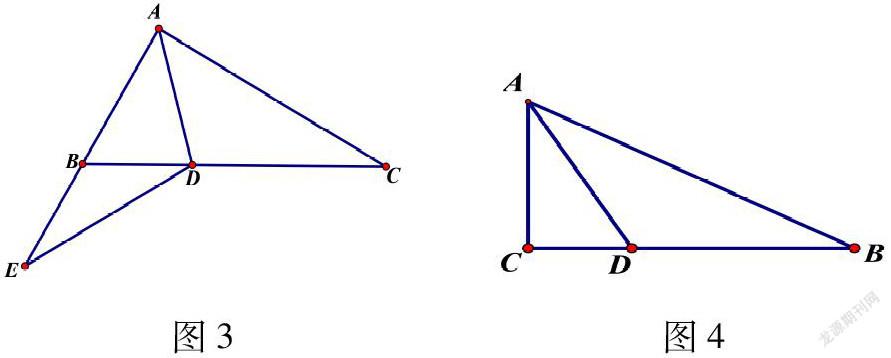
解法2（补短）在图3中，延长AB至AE，使得AE=AC，连接DE，根据AE=AC，AD是∠BAE的角平分线，AD公共边三个条件，判定△AED≌△ACD。从而把AC转化成AE，再由∠B=2∠C，∠C=∠E得到BD=BE，即AC=AB+BD。

问题1中，解法1和2从“截长”，“补短”两个途径给出了证明，追求了解决几何问题方法的多样性。但对于本题的探究，如果学生的思维成面只仅仅停留在利用“截长”和“补短”的方法来构造图形全等，还远远不够。不妨，我们再对问题1的变式展开探究。

变式：如图4，△ABC中，AD是∠CAB的角平分线，AD=BD，AB=2AC.求证：△ACB是直角三角形.

问题分析：立足题意证明目标是△ACB是直角三角形，根据角平分线与两对线段之间的关系，容易通过图形中的角度关系得到关联.在图4中，易得∠CAD=∠DAB=∠ABD。如何利用这三个角建立与∠C的联系，成为了解决问题最大的障碍。

由于此时的目标是角度，学生关联问题的思维很难与前面“截长”或“补短”建立联系。当然，在此题的本质仍然是“截”和“补”，但不同的问题情境，学生分析问题的思路却大相径庭。为何学生的思维会顿时失灵？两道同质类型的问题，前后竟有如此差异，足以引起我们的深思。

在问题1中，重新审视AD是角平分线这个条件.通常教学中，强调最多的是角平分线的性质以及它的判定条件，而对于轴对称图形中角平分线是对称轴的理解却不够。实际解题过程中对于角平分线的认知也仅仅停留在外在特征。从动态角度分析：角平分线把这个角的上下两个部分通过翻折能够重合。通过对角平分线的本质特征的介绍，渗透了“翻折”这一核心思想。学生对于角平分线能够认知这一思想后，无论是问题一还是变式，都能够结合图形利用翻折来转化线段与角度之间的数量关系，这样的解题方法更为自然。

方法巩固 如图，BC >AB，BD平分∠ ABC，∠ A+∠C=180°. 求证：AD=CD.

方法点拨：利用角平分线的对称性构造全等三角形。

解法1：如图6，BD平分∠ ABC，可将△ABD沿BD进行翻折，点A的对应点是点E，利用轴对称性可证△ABD≌△BED，易得AD=DE，∠ A=∠ BED，根据“等角的补角相等”可知∠ DEC=∠ C，证得AD=CD.

解法2：如图7，也可将△CBD沿BD进行翻折，构造△CBD≌△EBD，从而易证AD=CD.

解法3：利用角平分线的性质，作垂直，构造三角形全等，证明线段相等，这里不再赘述.

解后反思

1.反思解题方法，提高综合解题能力

数学问题，灵活多变，解题方法途径繁多。日常习题训练中，学生在解题时多半就题论题，满足于做出问题，对于解题方法的优劣不做评价，作业中的问题时常出现解题思路单一、逻辑错乱、描述冗长等问题。学生的思维如何打开，学生如何将自己已有的知识经验运用起来，这一切需要在日常教学中对于几何问题开展探究性学习，引导学生通过解题后形成自我的反思，优化解题过程，总结解题经验。在问题1的探究中，除却“截长”和“补短”两种方法的介绍外，还需渗透角平分线本质特征，“轴对称”的核心思想，真正能让学生学会解一题、通一法、联一片。

2.反思归类，举一反三，融会贯通

笔者在日常教学中，有意培养学生学会分析、比较不同问题中的类似点，探究共性，掌握规律。基于这一考虑，教学中设计的变式和方法巩固，引发学生对于同一种问题的思考，收获了解决这一类同质问题的技能，強化了几何中逻辑思维的训练。在几何解题教学中，教师必须引导学生进一步反思、分析方法的优劣，寻根溯源，努力找寻解决问题的“关键点”，对于类如“角平分线”这一问题，抓住问题的本市特征，不断提高和深化学生分析问题、概括问题、研究问题的能力，促使学生着眼于相互联系的数学知识体系，形成更为系统性的知识结构。

本文系2019年苏州市教育学会“十三五”教育科研规划课题 “数学实验在初中数学课堂中的实践研究”（课题编号：“十三·五”sjh[616]）的阶段性成果

苏州工业园区东沙湖实验中学 江苏苏州