基于函数型伸缩因子的桥式吊车变论域模糊PID控制器设计

邱光繁 徐进钊 邱炯智 张京玲 聂湛然 胡永刚

关键词：防摆定位控制;函数型伸缩因子;变论域;桥式吊车;模糊PID;非线性系统

0引言

桥式吊车作为一种重要的物料搬运工具，在车问、仓库、电厂等领域得到广泛应用，发挥着至关重要的作用。桥式吊车作业过程中会受到诸多因素的影响，比如风力、摩擦力以及小车牵引力的变化，会产生负载摆动，令桥式吊车的定位精确度和稳定性降低;另外，由于工作强度大、作业时间长，操作者需要长时问集中注意力，稍有疏忽就有可能引发安全事故。如何满足工程的实际需求和推进桥式吊车的安全应用，是桥式吊车控制研究的重要问题。

目前，桥式吊车的控制方式可以分为开环控制和闭环控制。最优控制、离线轨迹规划等是开环控制的代表方法，该类方法需事先给控制指令，无法应对作业过程中随机因素的影响，鲁棒性差，难以满足实际控制需求。针对此类问题，学者们提出了闭环控制算法，状态反馈、自适应控制、滑膜控制等，这类控制算法利用传感器返回的信号，实时地对系统进行调节控制，提高系统的鲁棒性。WANG W等提出了一种根据系统固有频率和阻尼比设计的滑膜控制器，仿真结果表明该控制可以很好地减少振动，且具有抗干扰能力较强、鲁棒性高的特点。Mon Y J等提出了一种分层模糊滑膜控制方法，将非线性系统分解为几个子系统，仿真结果表明分层模糊滑膜控制较传统的模糊滑模控制有更好的控制效果，进一步提高了控制器的魯棒性，但这些方法的控制准确十分依赖于起重机系统的数学模型，在实际中由于诸多因素的影响，难以对其数学模型进行精确建模。PID控制器调节整定不依赖系统的具体模型，结构简单，在工程中得到广泛应用。然而普通PID控制对于时变不确定性、非线性的系统控制，往往难以满足实际应用的需求，而模糊控制可以根据桥式吊车操作员的经验，建立模糊规则库，可以很好地模仿桥式吊车操作员的控制。

为此本文提出一种基于函数型伸缩因子的模糊自适应PID控制策略，该方法保留PID简单、快速以及运算量较小的优势，同时具有普通模糊处理非精确数学模型的特点，通过论域自适应调整，控制精度比普通模糊更高。提出了一种待控参数数量适于工程软件处理的函数模型的伸缩因子，替代常见的伸缩因子实时对论域进行自适应调节，这种伸缩因子只需要控制一个参数，减轻工程软件运算压力，从而提高控制精度和控制实时性。通过仿真实验结果表明该方法的控制效果优于PID和模糊PID两种方法，并对外界扰动具有较强的稳定性。

1桥式吊车模型建立

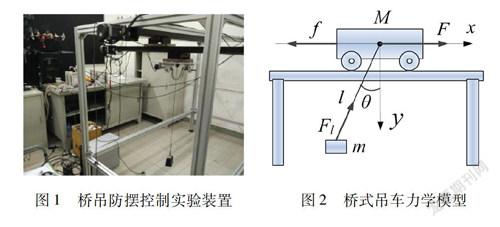
由桥吊防摆控制实验装置如图1所示。小车质量为M，存在水平方向的牵引力F以及阻力f，阻力系数为μ，负载质量为m，绳索长度为l。忽略绳索的质量、绳的弹性形变、空气阻力、风力、吊绳与台车连接处的摩擦力等。建立直角坐标系：X轴正方向为力的方向，垂直地面向下为Y轴正方向，设负载与台车的坐标分别为，负载摆角为，绳长为l，水平方向位移为x，建立二维坐标下的桥式吊车模型如图2所示。

由图2可知，台车和负载的位置坐标为：

利用拉格朗日法建立桥式吊车系统的动力学方程得桥式吊车系统的动力学模型：

2变论域模糊自适应PID控制器设计

由式（2）可以看出，桥式吊车系统位移x和摆角仅由输入量F控制。为了得到适合的控制量F，使得位移x快速精确定位且要令摆角的摆动幅度减少，对桥式吊车模型设置变论域自适应PID模糊控制器，以实现桥式吊车的防摆定位控制。

2.1PID控制器设计

常规PID控制器具有应用广泛、使用灵活、容易实现等优点。PID模块的传递函数为：

2.2模糊自适应PID控制器

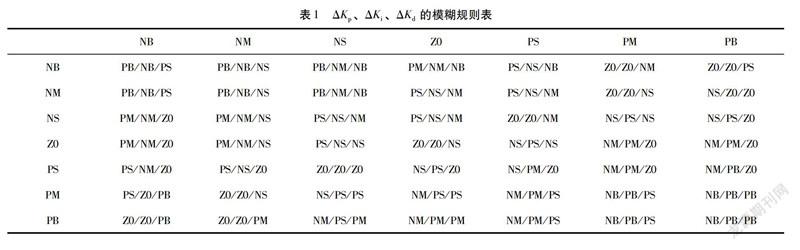
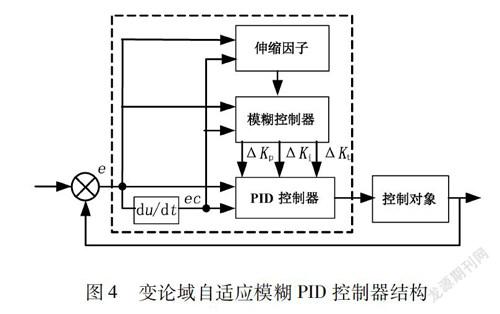
将误差e和误差变化率ec传入由专家经验所建立的规则库的模糊器，通过模糊推理，解模糊化最终得出输出信号值，其中，根据实际情况，输入变量e和ec的模糊子集分别记为{负大，负中，负小，零，正小，正中，正大}，记为{NB，NM，NS，ZO，PS，PM，PB}，误差e和误差变化率ec的模糊论域均为（-3，3）。输出变量△K，△K，△K的模糊子集分别为{负大，负中，负小，零，正小，正中，正大}，记为{NB，NM，NS，ZO，PS，PM，PB}，输出变量AK，△K，△K的模糊论域分别为（-0.3，0.3），（-0.06，0.06），（-3，3），采用”if…then…”制定模糊规则。模糊自适应PID控制器的本质还是PID控制，与单PID控制器的区别是，模糊自适应PID借助模糊规则（表1），实时对PID参数进行调节，这是模糊自适应PID控制器的基本控制策略。为了系统的稳定，在开始时给定PID参数的初始值，所以PID参数为初始参数加上模糊调整参数：

2.3基于函数模型的伸缩因子

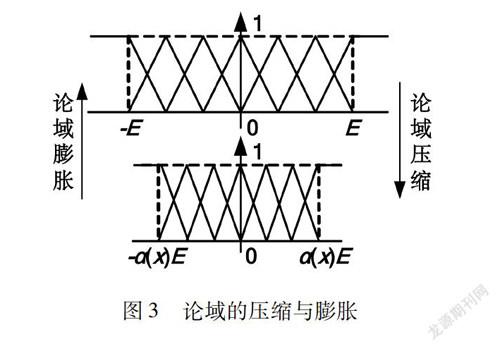
在模糊控制器的基础上加上函数模型伸缩因子来调整论域，如图3所示，伸缩后论域为a（x）[-E，E]，β（x）[-E，E]。伸缩因子的计算主要有2种方法，本文采用基于函数模型的伸缩因子，通过以误差和误差变化率为参数的函数来产生伸缩因子，变论域自适应模糊PID控制器结构如图4所示，函数模型产生伸缩因子的主要形式有：

上述函数型伸缩因子被许多学者应用到MATLAB仿真，然而实际工程控制器的实时运算处理能力比MATLAB弱，难以保证控制输出的实时性。式（7）～（8）需要控制2个参数，式（9）每一次都需要进行求和积分操作，对软件的计算能力要求高。

选取式（10）作为输入论域的伸缩因子参数函数，根据PID控制器3个参数对控制性能的影响，K和K的伸缩因子应与误差单调一致，K的伸缩因子应该与误差单调反向，故选取：

3仿真与分析

为了评定变论域模糊自适应PID控制器的控制性能，利用上述PID控制器、模糊自适应PID控制器、变论域模糊自适应PID控制器分别在MATLAB中按照表2桥式吊车参数和表3控制器设置参数的数据建立仿真模型进行仿真实验。

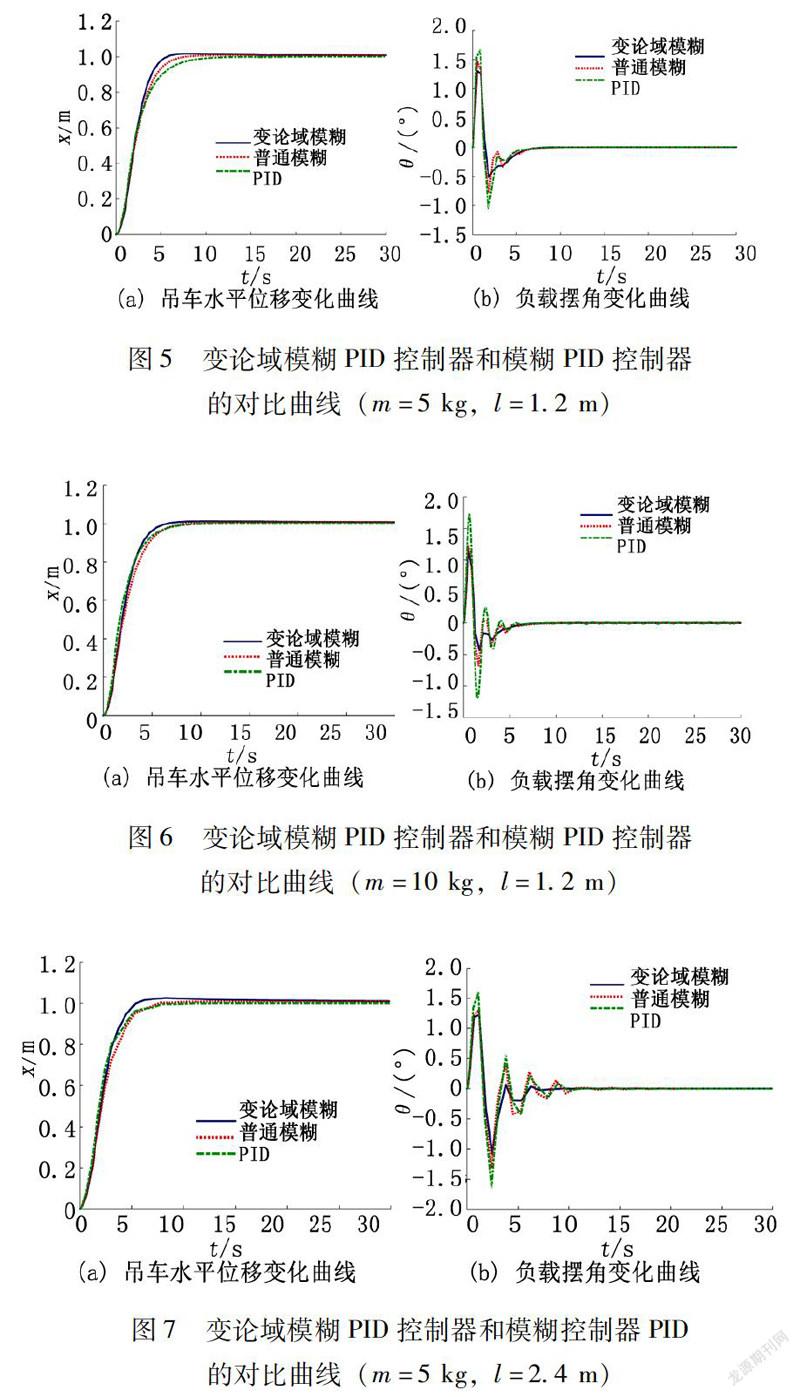
得到绳长和负载质量发生改变时的一组变论域模糊控制器和模糊控制器的对比曲线：图5～7所示分别为不同的绳长和负载的位置和摆角的无干扰仿真图，图8所示为3个控制器的抗扰动控制仿真曲线。从图5-7可以看出，在相同条件下，3种控制器的位移控制曲线，变论域模糊控制器收敛更快。3种控制器对摆角的抑制效果有明显的差异，在变论域模糊控制器的控制下，角度峰值较低，对负载摆动抑制效果高于另外2种控制器。桥式吊车实际工作过程中，常会受到外界因素的干扰，因此需要控制器有较强的抗干扰能力，为比较上述3种控制器的抗干扰力，在15-17s时，在控制器中加入脉冲宽度为2s的0.01rad的脉冲干扰。由图8可知，PID控制器在19.42s恢复稳定，普通模糊控制器在19.31s恢复稳定，变论域模糊控制器在18.34s恢复稳定，变论域模糊控制器的受干扰程度较普通模糊自适应PID控制器和PID控制器较小，抗干扰能力更强。本文提出的控制器相比于普通模糊自适应PID控制器和PID控制器能更好地对小车进行精确定位和负载的防摆控制，并且该控制器对于系统参数的变化具有一定的适应力，同时鲁棒性和抗干扰能力更强。

4结束语

针对桥式吊车系统的防摆定位控制问题，本文提出一种新的函数模型伸缩因子，并成功将变论域模糊自适应PID控制策略成功应用到桥式吊车系统的防摆定位控制中，该策略保留PID简单、快速以及运算量较小的优势，同时具有普通模糊处理非精确数学模型的特点。利用本文提出的函数模型伸缩因子对论域进行自适应调节，提高控制器的精确度，很好地实现了桥式吊车小车的精确控制与负载摆动的有效抑制。仿真结果表明，本文提出的控制器较普通的模糊控制器和PID控制器具有更好的控制效果，并且该控制器对于系统参数的变化具有一定的适应力，对环境随机因素的干扰也有很好的抵抗力，同时系统鲁棒性更强。