改进移动闭塞方式多列车运行粒子群优化算法

2021-09-10翁兆奇

内燃机与配件 2021年3期

翁兆奇

摘要：闭塞是多列车运行必须要考虑的重要问题。为了提升移动闭塞方式下的多列车运行的闭塞效果，本文提出了一种改进的粒子群算法（Improved Particle Swarm Optimization Algorithm，IPSO）。采用粒子群算法与遗传进化相结合的方式，以有效提升粒子群算法的全局寻优能力。具体的移动闭塞方式下的多列车运行优化算例的仿真结果表明，本文提出的改进的粒子群优化算法具有较佳的优化效果，适合于解决移动闭塞方式下的多列车运行优化问题。

关键词：移动闭塞;多列车运行;粒子群优化算法;遗传进化

Abstract： Block is an important problem that must be considered in the operation of multiple trains. To improve the blocking effect of multi-train operation under the moving blocking mode， this work proposes an improved particle swarm optimization algorithm （IPSO）. The combination of particle swarm optimization and genetic evolution is introduced to improve the global optimization ability of particle swarm optimization. The simulation results of multi-train operation optimization under the moving block mode show that the IPSO algorithm proposed in this paper has better optimization effect and is suitable for solving the multi-train operation optimization problem under the moving block mode.

0 引言

閉塞系统在城市轨道交通运营中扮演着非常重要的角色[1]。随着现代轨道交通事业的大力发展，闭塞效果差导致的乘客对铁路运营商的矛盾也日益引发人们的关注和重视。因此，需要尽可能的提升闭塞效果。然而，由于移动闭塞方式下的多列车运行优化问题需要考虑众多的因素，且实际问题中具有大量复杂的各类因素[2]。由此可知，移动闭塞方式下的多列车运行优化问题极难求得理想的满意解。

目前，移动闭塞方式下的多列车运行优化的相关算法改进策略已成为相关科研人员的研究重点。至今为止，已经有大量的研究应用于实际的移动闭塞方式下的多列车运行优化问题中。田志鹏[3]研究了移动自动闭塞的列车追踪控制优化模型及其算法。罗志刚[4]研究了列车安全距离的优化以及列车追踪运行的调整策略。朱咏秋[5]研究了基于北斗二代的移动闭塞条件下的列车运行组织方法。唐海川[6]研究了地铁列车追踪运行的节能控制。赵明[7]研究了移动自动闭塞条件下的列车追踪运行控制算法。以上研究能够对部分移动闭塞方式下的多列车运行优化问题解决有相当程度的帮助，但仍然存在着算法寻优效果不够理想的问题。

移动闭塞方式下的多列车运行优化是一个复杂的实际工程优化问题，难于求得令人满意的优化解。然而，目前提出的大量的智能优化改进算法，存在着易于陷入局部极小值的问题。针对这一问题，为提高智能优化算法的全局收敛性能以便于更好的解决移动闭塞方式下的多列车运行优化问题，本文提出了一种改进的粒子群优化算法。为验证改进算法的有效性，本文基于2种测试函数采用不同算法进行仿真试验。试验结果表明，本文提出的改进算法具有更佳的算法性能。在此基础上，本文采用移动闭塞方式下的多列车运行仿真算例进行仿真验证，并采用了本文提出的改进的粒子群优化算法，其仿真结果能够表明，本文提出的改进的粒子群优化算法能够有效的提升移动闭塞方式的闭塞效果。

1 移动闭塞方式下多列车运行理论

1.1 移动闭塞信号系统

迄今为止，在各类系统中最高的列车线路能力利用效率，是移动闭塞的行车闭塞方式。而与固定闭塞方式相比，移动闭塞就相当于将区间，分成了无数个细小连续的闭塞分区，但没有划分固定的闭塞区间。它使得列车间的安全信息传递得更为及时和频繁。移动闭塞中列车速度限制可以有以下几种情况：

1.1.1 前行列车速度vF不小于后行车速度vB

此时，两列车间的距离原则上，越来越大，理论上前行列车对后行列车应无约束。但从安全角度来看，要保证万一前行列车发生事故，或闭塞设备发生故障时，后行列车能及时停车并不至于与前行车相撞。当vF？叟vB时，列车间的最小间距为：

公式（1）中，LB为后行车的常用制动距离，LA为紧急情况出现时司机采取制动时所需反应时间内列车的走行距离，LS制动停车后后行车头与前行车尾部的安全距离，L1为列车长度。

1.1.2 前行列车速度vF小于后行车速度vB

当前行列车速度低于后行车时，两车的距离将越来越近。此时，列车相距越远，速度限制越弱，在后行车前方存在一个常用制动曲线。当后行车在空间上闯入这一曲线时，闭塞要求后行列车采用常用制动，以保证行车安全。

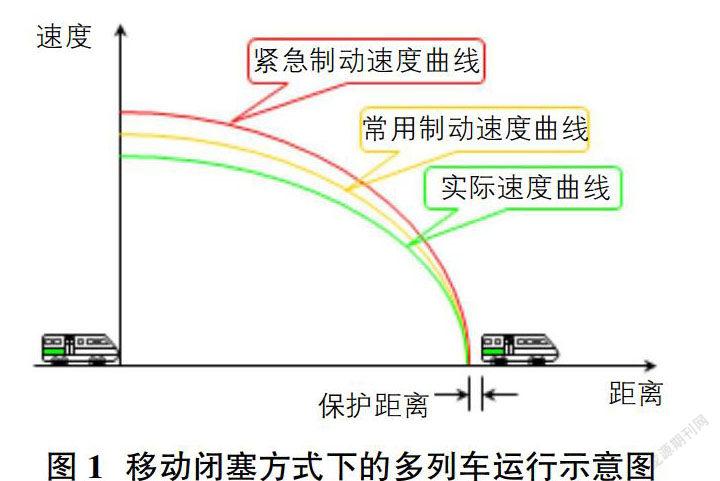
具体的移动闭塞方式下的多列车运行示意图如图1所示。

1.2 移动闭塞方式下的多列车运行计算

移动闭塞下多列车运行计算中最重要的部分，就是由限速曲线将信号限速替换掉，而这个限速曲线是由前行车位置，与后行车制动距离等因素确定的。移动闭塞也按上述原理设计，在设计移动闭塞计算过程中应当注意下面几个方面：①根据前行列车的运行，后行列车的限速向前连续变化，而不再是按前行列车所清空的轨道电路变化，这与准移动闭塞系统不同。②后行列车的目标限速点，只于前行列车的安全距离和尾部位置有关，而不再考虑前行列车所占用的轨道电路。③没有必要对轨道电路的长度和位置进行标识，因为移动闭塞没有划分轨道电路分区。

2 改进的粒子群优化算法

2.1 基本粒子群算法

2.2 自适应变异策略

由于算法计算过程中，特别是迭代计算的后期，粒子群算法容易受到最优个体的影响。为此，将遗传进化机制引入粒子群算法有助于一定程度的增强其种群多样性，从而有利于提高粒子群算法的全局搜索能力和收敛速度。

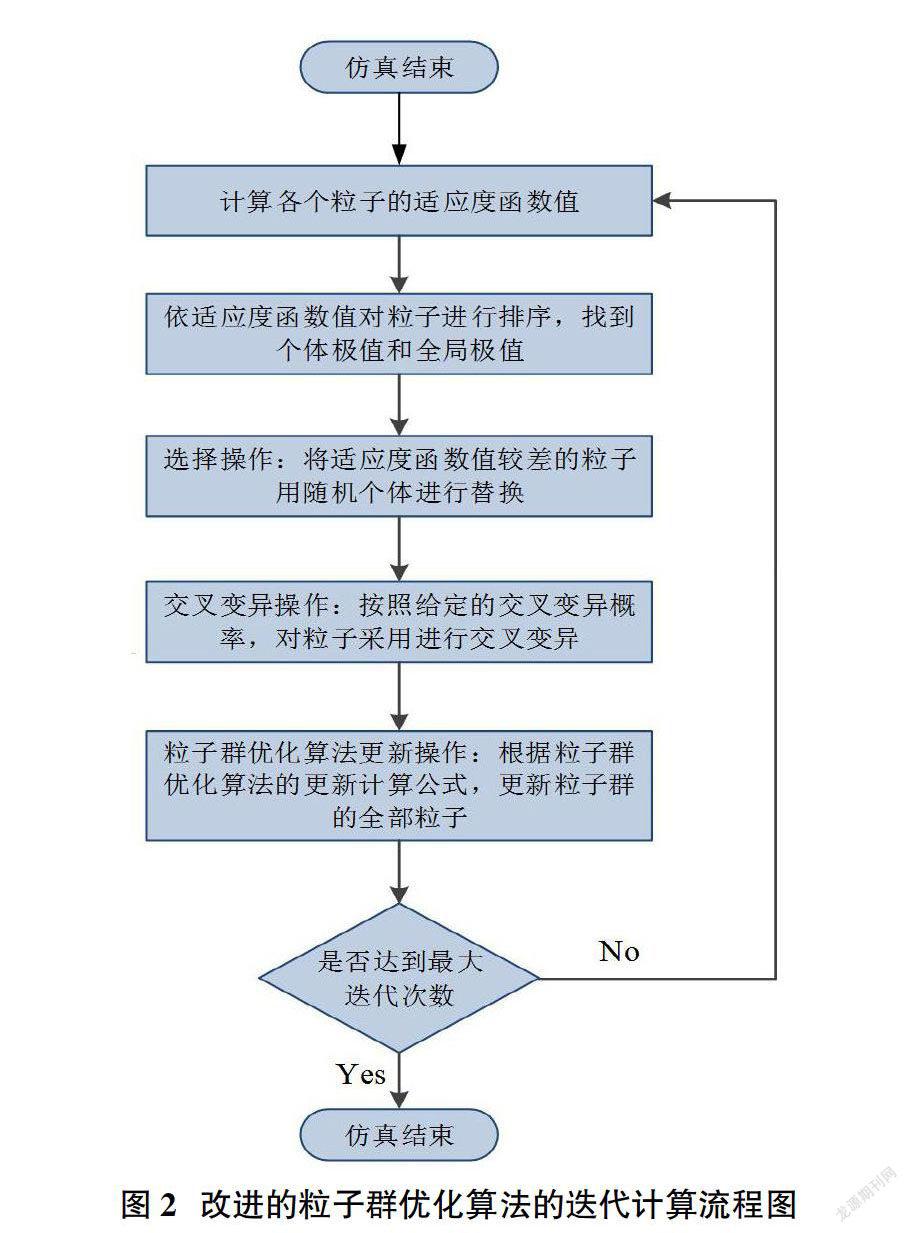
本文提出的改进的粒子群优化算法的迭代计算流程如图2所示。

3 仿真实验

3.1 基于移动闭塞方式下的多列車运行优化仿真参数

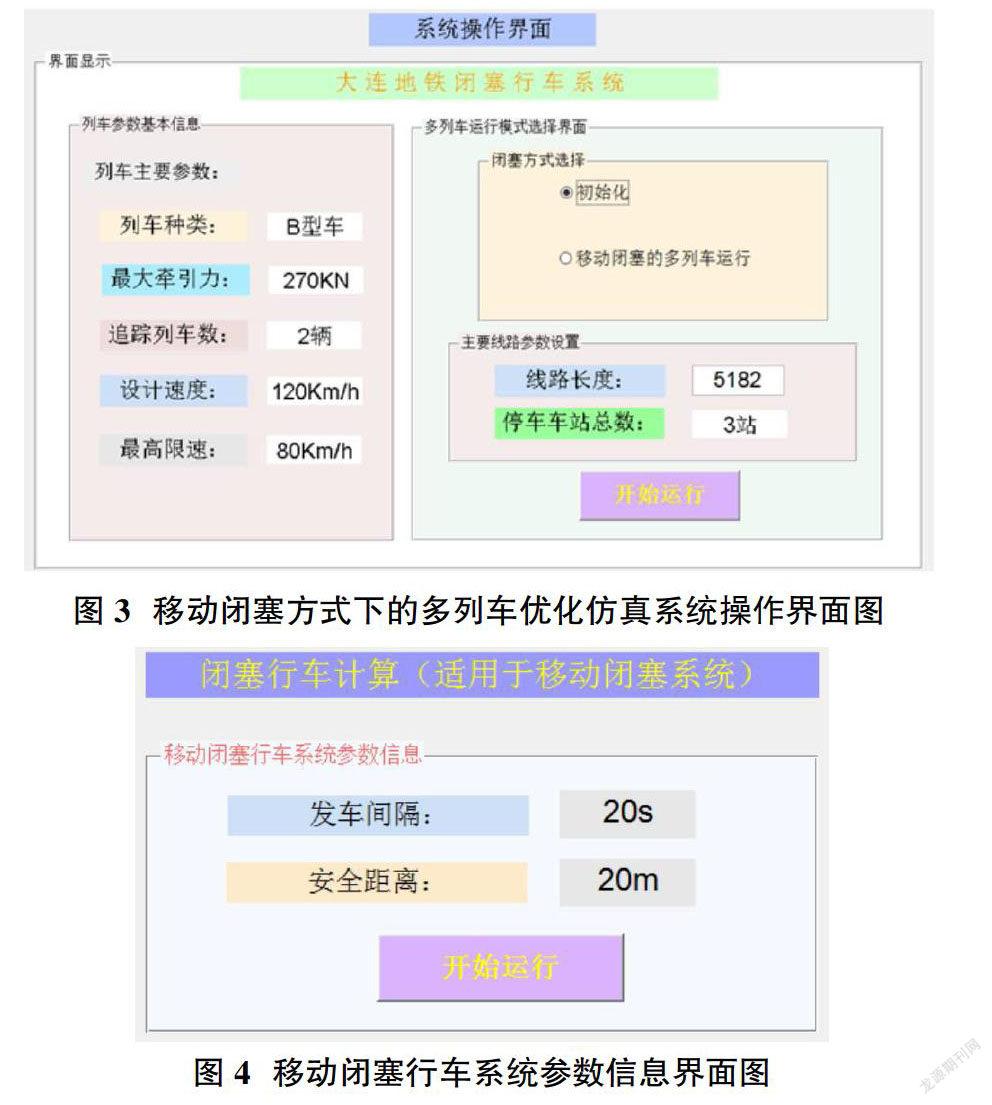
本文采用移动闭塞方式下的多列车运行仿真算例进行仿真验证，所选用的优化算法为本文提出的改进的粒子群优化算法。本文选取大连3号线地铁车辆作为研究对象，将从九里站经停十九局站到达和平路站这一段运行线路作为实验线路。具体的移动闭塞方式下的多列车优化仿真系统操作界面和移动闭塞行车系统参数信息界面如图3和图4所示。

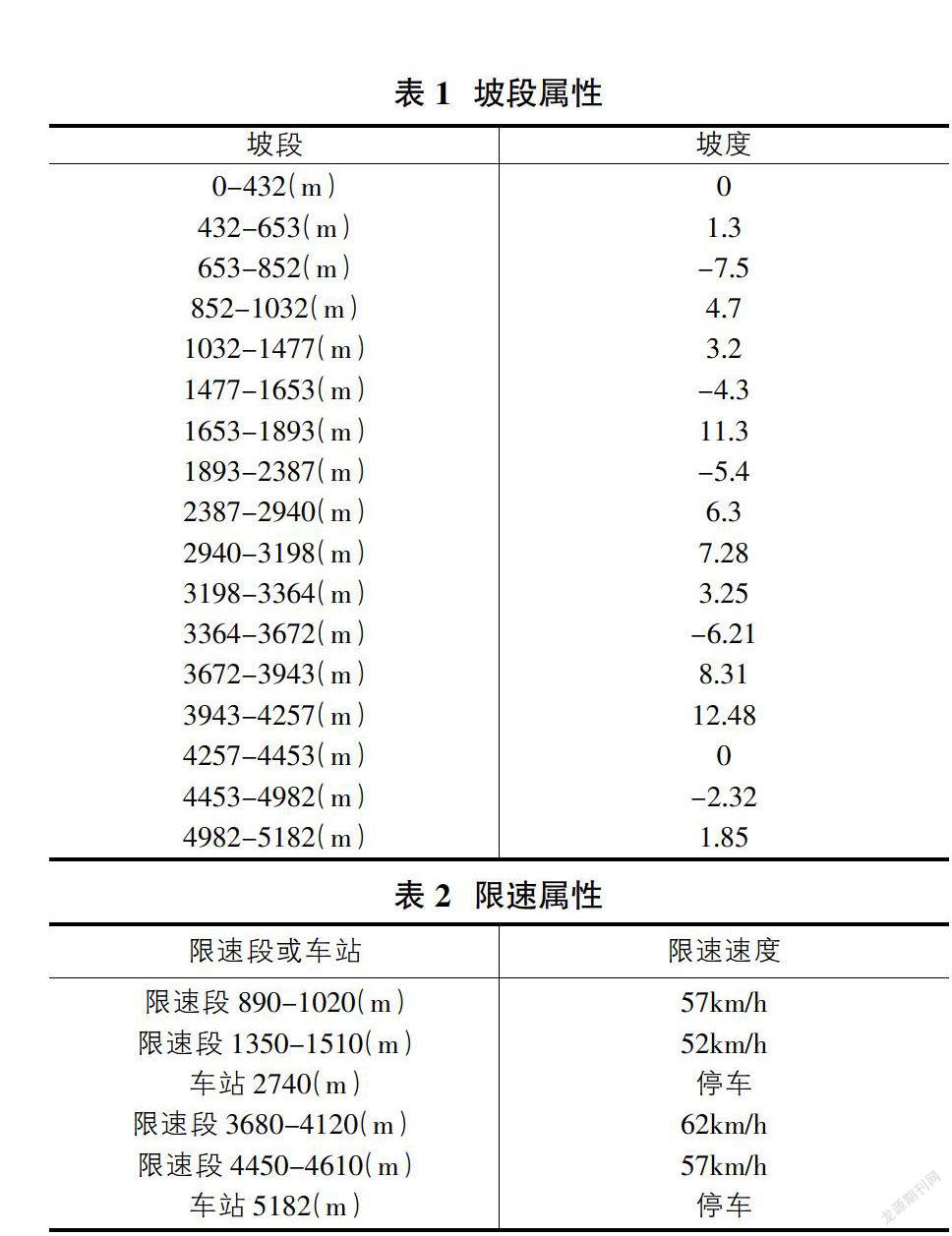
具体的坡段属性及限速属性如表1和表2所示。

3.2 基于移动闭塞方式下的多列车运行优化仿真结果

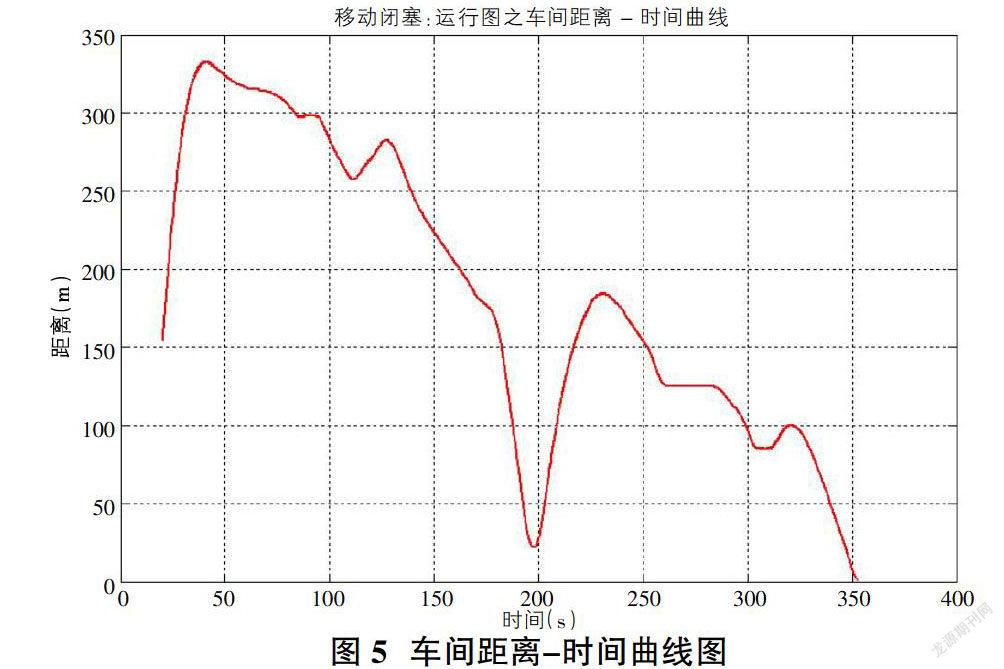
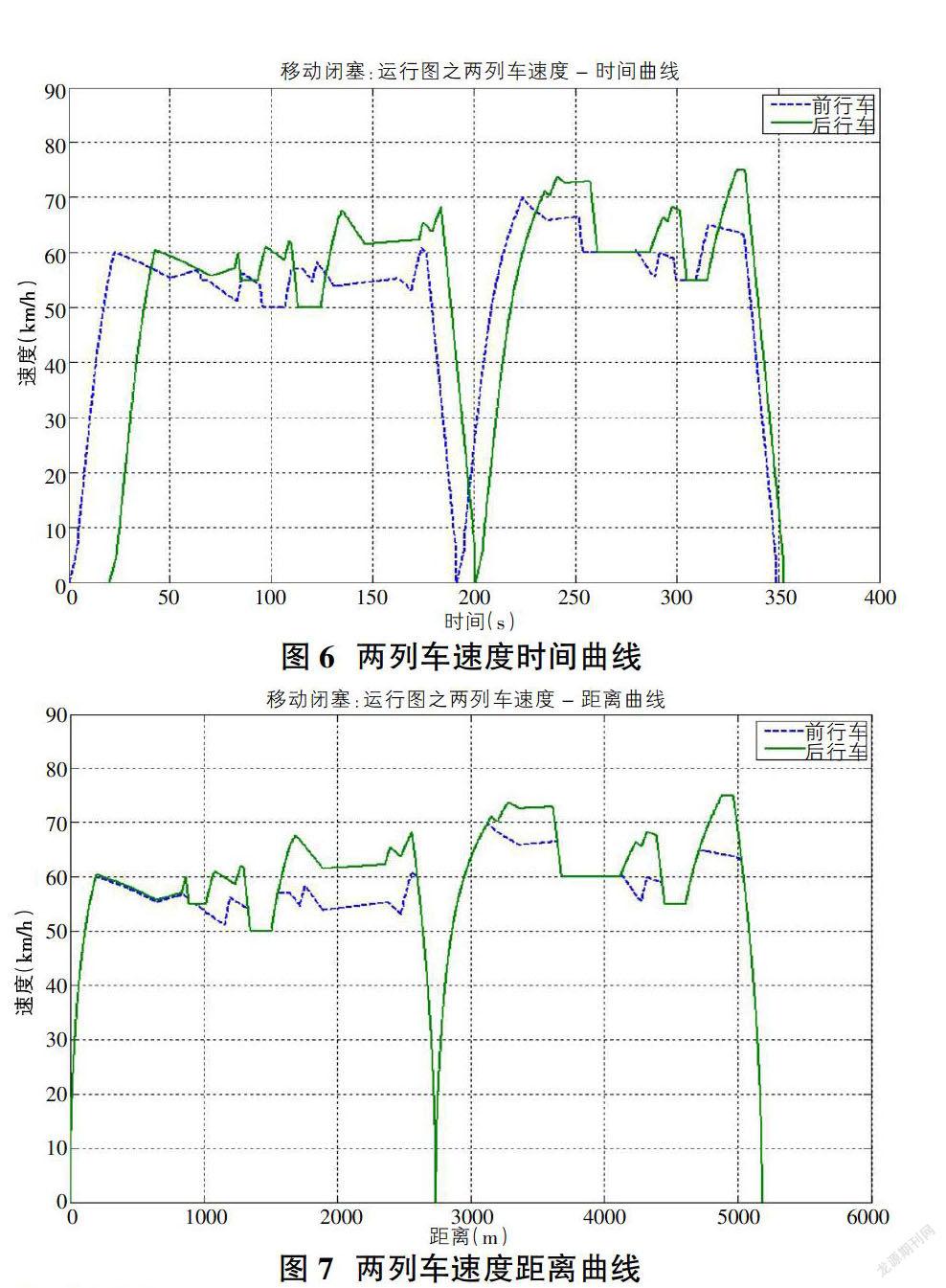
由于没有固定闭塞分区的限制，前行车与后行车之间的运行状态是通过信号设备进行数字信息交换来进行的。后行车可以根据前行车传输的数据而对本车的速度进行实时调整，所以两辆车之间的追踪距离，会在保证行车安全的基础之上有很大的缩小，在路程的后半段会明显体现出来。具体的移动闭塞方式下的多列车运行仿真的结果曲线如图5-图7所述。

由图5的车间距离时间曲线可知，与预期效果相符，在路程的后半段，在保证行车安全的基础之上有车间距离有很大程度的缩小。这表明，采用本文提出的改进算法进行优化，能够一定程度的提升移动闭塞的闭塞效果，从而提高通行能力。由图6和图7可知，后行车具有较强的追踪能力，这也从侧面一定程度的反映了本文所提算法的有效性。

4 结论

为了提升移动闭塞方式下的多列车运行的闭塞效果，本文提出了一种改进的粒子群优化算法（IPSO）。通过引入遗传进化机制来有效提高粒子群算法的全局搜索能力和收敛速度。

本文采用移动闭塞方式下的多列车运行仿真算例进行仿真验证，并采用了本文提出的改进的粒子群优化算法，其仿真结果能够表明，本文提出的改进的粒子群优化算法（IPSO）能够有效的提升移动闭塞方式的闭塞能力，以提高通行能力。

参考文献：

[1]刘海东.不同闭塞方式下城轨列车追踪运行过程及其仿真系统的研究[J].铁道学报，2005（02）：120-113.

[2]路飞.移动闭塞条件下地铁列车的运行优化[D].济南：山东大学，2007，4.

[3]田志鹏.移动自动闭塞的列车追踪控制优化研究[D].兰州：兰州交通大学，2016，6.

[4]罗志刚.列车安全距离优化及追踪运行调整策略研究[D].兰州：兰州交通大学，2015.

[5]朱咏秋.基于北斗二代的移动自动闭塞下列车运行组织方法研究[D].成都：西南交通大学，2015.

[6]唐海川，王青元，冯晓云.地铁列车追踪运行的节能控制与分析[J].铁道学报，2015（01）：37-43.

[7]赵明，汪希时.移动自动闭塞条件下列车追踪运行控制研究[J].铁道学报，2011（03）：62-69.

[8]Kennedy J， Eberhart R C. Particle swarm optimization[A]. Proceedingsof IEEE International Conference on Neural Networks[C]. 1995， 1942-1948.