关于平行线段与延长线段相等规律的猜想
2021-09-10高漾
小作家报·教研博览 2021年5期
高漾
中图分类号:G4 文献标识码:A 文章编号:(2021)-5-013
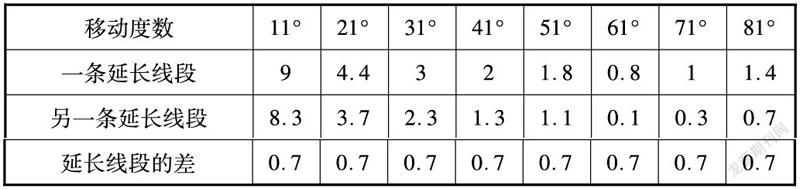
猜想:如果有两条相互平行的等距离线段,且两条线段中间的距离是一个定值,如果将一条线段移动相对的度数,另一条线段度数不变,延长线段相交于一点,那么两条延长线之间的差是定值。(两条平行線段长度一样)
用以上数据体验,如果相交点在一条线段上,用第一条的延长线的相交顶点左半部分的差,即小于90°的,反之,右部分的差)若不出现定值,会不会有规律的数字?(此猜想可能与90度无关)
证实:我以2厘米的一组平行线段并且它们之间的距离同为2厘米且做了一验。注:移动的度数要小于90度
结论:可以设两条线段的长度为x 厘米,两条线段的距离为y厘米。一条线段旋转的度数为Z°
1,X与Y为定值, Z为不定值。
2,X与Z为定值,Y为不定值。
3,Y与Z为定值,X为不定值。
4,Z为定值,X与Y为不定值。
5,Y为定值,X与Z是不定值。
6,X为定值,Y与Z是不定值。
它们延长线段之间会出现差,差为定值。或者为倍数关系。
作用:找出内在的关系可以方便我们在一些建筑工程的实施。可以直接找到它们两条线段的交点。用规律节省时间也不会因刻度尺有限而无法进行研究。
指导教师:兰亚辉
怀仁七中 山西 怀仁
