促进学生积累数学基本活动经验的有效策略

吴存明

数学基本活动经验是《义务教育数学课程标准（2011年版）》明确提出的一个学习目标，它与数学基础知识、数学基本技能、数学基本思想成为同等重要的教学要素。其中，数学基本活动经验尤其受到教育学者和一线教师的关注。笔者认为，数学基本活动经验是指学生参与数学知识的发现和发明过程中的经历、体验，以及在数学操作活动过程中所形成的认知和情感。在小学数学教学中，教师如何引导学生积累数学基本活动经验？本文拟结合教学实践，从三个方面探寻促进学生积累数学基本活动经验的有效策略。

一、建构框架是积累数学基本活动经验的前提

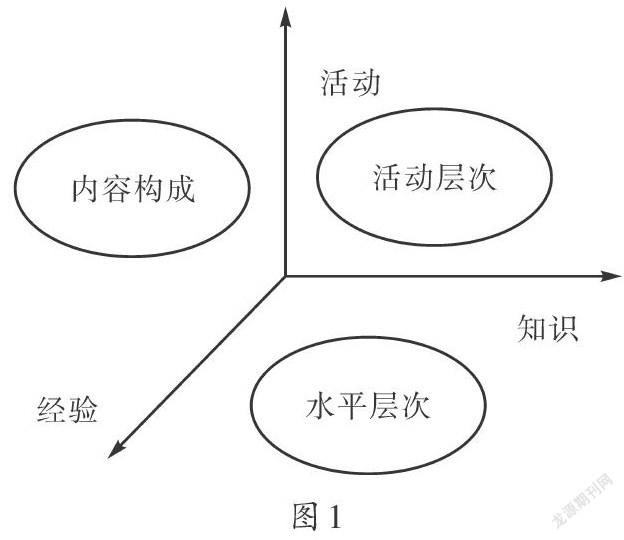
促进学生积累数学基本活动经验，教师首先要思考经验与知识、活动三者之间的关联性。数学基本活动经验有其特殊性，首先是基于特定的数学知识，即以数学教材为文本的特定内容，其次是基于特定的群体，即学习方式以活动为主的小学生群体。因此，只有针对特定的数学知识和数学活动，才能让数学经验具体化，在此基础上，数学基本活动经验的积累才成为可能，发展学生的数学思维才能成为现实。从有利于教师把握和实施教学的角度，笔者尝试把知识、活动和经验分离开来，作为研究的三个维度（如图1）。

小学数学不同领域的知识内容对学生经验的需求是不同的，不同的知识内容决定了课堂中学生需要经历哪些数学活动，而这些数学活动又直接作用于学生经验的激活、呈现、修正与提升。数学知识与数学活动的这种相互影响，决定了经验的复杂性，因此，我们很难对经验进行严格的划分，专家们对此分类也不尽相同。

综合已有经验类型的研究成果，我们大致可以将经验分为操作性活动经验、策略性活动经验和观念性活动经验三种类型。具体而言，操作性活动经验主要是个人直接参加或者从观察等实践活动中获得知识和技能，由直观性较强的形象生动的心智图像、特殊的案例、特别的场景等构成;策略性活动经验是指学生解决问题过程中得到的具体策略方面的经验（如比较、转化等）以及一些创造性经验（如归纳、类比、想象等）;观念性经验是在应用已有经验的过程中产生的经验的系统化和逻辑化并上升到数学思想层面的认识和感受（如恒等变形、统一单位的意识和思想等）。基于上述分析，笔者将上述的三维框架细化为图2。

二、设计活动是促进学生积累数学基本活动经验的关键

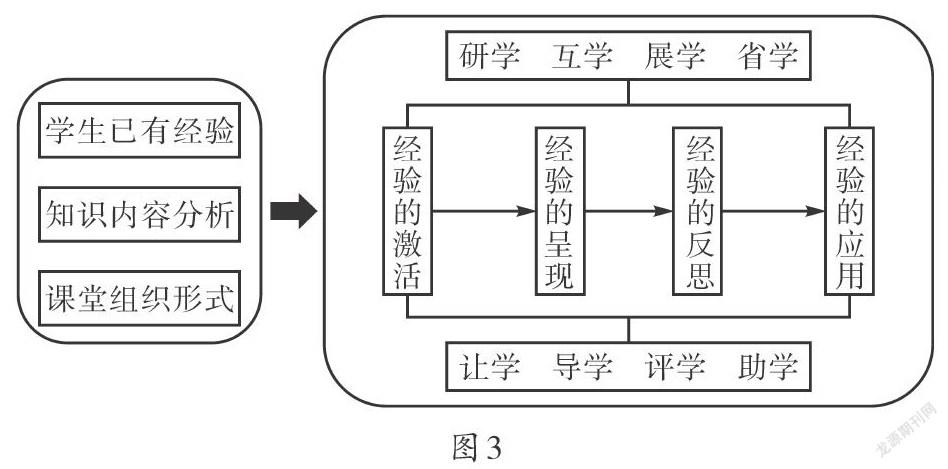
促进学生积累数学基本活动经验的关键，是教师要能够设计一项或几项数学学习活动并有效开展这些活动。在三维框架（如图3）基础上，结合课堂教学实际，教师可以设计和实施相应的数学学习活动。

以上数学活动实施框架包含了学习活动前的准备、学习活动的设计与实施两部分内容。数学学习活动正式实施前的准备工作主要是，教师根据所学知识内容，分析学生已有的知识与活动经验，确定课堂学习活动的形式，根据学生的学情设计数学学习活动。在数学学习活动实施过程中，学生需要经历经验的暴露、生成、提升与应用四个环节，这四个环节层层递进，循环往复。在此过程中，教师需要注意两个方面的教学。

（一）根据知识的不同属性确定不同的学习路径

这个教学环节需要解决“学什么”的问题。数学课程的知识大致可以分为两种类型。一种是根据人的需要与主观意愿发明和创造出来的数学知识，如“竖式”就是人们为了减轻计算时的思维负担所创造出来的记录计算过程的一種方式。这一类知识的本质是“发明”，可以称为“规则性知识”。另一种是对客观存在的规律的描述与判断。这一类知识的特点是具有“确定性”，不以人的主观意志为转移，如“平行四边形的面积”这一知识点反映的就是一个平行四边形面积大小与这个平行四边形内部元素（底边长度和高的长度）之间相互依存与制约的关系。这一类知识的本质属性是“发现”，可以称为“规律性知识”。

“发明”的知识与“发现”的知识属性不一样，因此，学习方式也存在差异。

“发明”的过程侧重“需求与创造”，一般需要经历感受需求、自主发明、多样比较、统一规则、关联与应用等过程。如，教学《用数对确定位置》一课，教师可以设计如下3项数学活动，活动流程与认识点一一对应：活动1是“研学”，出示教室座位图，提问学生“小军在教室的位置应该怎样表示”，要求学生独立完成，旨在让学生感受需求、自主发明;活动2是“展学”，通过讨论、交流和分享大家对小军所在教室位置的描述，确定最佳方案，旨在通过多样比较，统一规则;活动3是“评学”，如要求学生先表示出小明在教室的位置，再根据数对找到人的位置，旨在实现关联与应用的教学目标。

“发现”的过程注重“观察与比较”，在设计数学学习活动时，教师一般要考虑观察的动机和对象，让学生经历观察与比较、关联与应用等过程。如，教学《间隔排列》一课，教师可以设计如下3项数学活动，活动流程与认识点也要一一对应：活动1是“研学”，出示两组物体的排列，请学生观察并“发现”物体排列的特点是什么（教师提示：一一间隔排列），目的是呈现观察的动机;活动2是“研学与展学”，让学生观察更多的一一间隔排列，从量的角度去比较、分类，目的是学会观察与比较;活动3是“评学”，用□与△创造一个或几个一一间隔排列，提问学生“当□有10个时，△可能有几个”，目的是实现关联与应用。

（二）让学生经历数学基本活动经验的四个阶段

促进学生积累数学基本活动经验，教师必须让学生充分经历经验的激活、经验的呈现、经验的反思、经验的应用四个阶段。“经验的激活”是指教师设计数学学习活动，学生开展数学学习活动，学生之间不交流，各自独立思考，实现原有经验的激活，这是积累数学基本活动经验的前提。“经验的呈现”是指在经验暴露的基础上，学生之间合作交流，在听讲、观察的过程中，实现原有经验与他人经验在头脑中的碰撞。“经验的反思”是指教师根据学生的学习情况，引导学生对已有的经验进行筛选、整理、优化和提升，实现经验的改造或重组，形成再生经验，促使经验上升到更高水平，让片面的经验变得完善，让模糊的经验变得清晰，让错误的经验变得正确，让零散的经验变得结构化。“经验的应用”是指学生原有经验是否获得提升，需要通过解决问题进行验证，并在应用中巩固和发展经验，将经验进行提炼、升华，积累新的经验。

以《认识角》一课为例，教师可以设计如下学习活动对应经验的激活、呈现、反思、应用四个阶段：在“经验的激活”阶段，可以设计数学学习活动“画角”，要求学生独立思考：你认为什么是角？请你把心目中的角画在纸上，目的是了解学生对角的认识情况，区分生活中的角与数学中的角，暴露已有的数学经验。在“经验的呈现”阶段，教师可以设计数学学习活动“摸角”，要求学生在布袋里摸出带有角的物体（布袋里有吸管、毛线、两把三角尺、图钉、圆纸片等），目的是让学生感受角的特征，建立数学中角的模型，生成新的经验。在“经验的反思”阶段，教师可以设计数学学习活动“做角”，让学生比较角的大小，开展合作交流，如利用没有角的材料创造角、教师示范通过伸缩的天线创造角，目的是让学生依据角的特征创造数学的角，获得经验的提升，发展学生的对比经验和创造性经验。在“经验的应用”阶段，教师可以设计数学学习活动“数角”，如一个长方形有几个角？减去一个角，还有几个角？请你试着画一画。目的是让学生综合运用新生成的经验，数一数角的个数。

三、教师引领是促进学生积累数学基本活动经验的保障

拥有良好的学习活动设计，如何实施才能帮助学生有效积累数学基本活动经验呢？一方面，教师需要克服自己片面的认识，如：只要学生动了，教学就是有活动;一节课中，学生经历的操作活动越多越好;学生参与数学活动的时间越长越好;等等。另一方面，教师要积极发挥促进学生积累数学基本活动经验的引领作用，给予学生充分的学习时间和空间、引导学生自主学习、诊断学生的学习过程和结果，概而言之就是让学、導学、评学、助学。

还是以《认识角》一课为例。首先，教师要给予学生充裕的学习时间和空间，放手让学生“画角”“摸角”“做角”“数角”，鼓励学生动手操作、实验、观察、推理、想象，这个过程就是“让学”。其次，学生在动手操作过程中遇到困难时，教师要善于设置疑问、启发思维、引导过渡，此为“导学”。最后，角的大小与什么有关呢？在“做角”过程中，教师会发现，学生眼中“角的大小”指的是图形面积的大小（把“角”看成一个封闭的图形，面积越大角越大）。对于学生这种不正确的认知，教师要及时进行纠正：可以让学生创造一个和教师做的天线角一样大小的角，再创造一个比教师的天线角还要大一些的角，运用“叠合”的方法直观确认，从而学会比较，积累比较的数学经验，此为“评学”和“助学”。

综上所述，为促进学生积累数学基本活动经验，教师需要基于三维框架设计数学学习活动，引导学生在数学学习过程中经历人类发现和发明数学知识的过程，让学生像发明家或数学家那样去思考数学问题。数学基本活动经验积累得多了，学生的数学思维和数学核心素养也就自然而然地培养起来了。

注：本文为江苏省教育科学“十三五”规划课题“深度学习视域下小学数学理解性学习的实践研究”（课题编号：Xc-b/2020/07）的阶段性研究成果。

（责编 欧孔群）