基于GARCH模型的股指期货期现套利实证研究

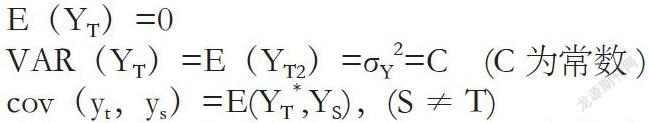
摘要：本文在期货统计套利策略基础上，设计了一种基于GARCH模型的时变方差套利策略，并利用沪深300指数与期货的日收盘价格进行实证分析，研究发现：目前国内股指期货市场存在较多的期现套利机会，市场有效性缺失，且基于GARCH模型的时变方差统计套利策略能详细得出期现套利机会。

关键词：GARCH模型;成本定价模型;期现套利;股指期货

股票指数期货是金融期货中产生最晚的一个类别，中国金融期货交易所于2006年9月8日在上海正式成立，它标志着中国股指期货市场登上了全新的台阶。股指期货具有跨期性、杠杆性、联动性以及高风险性和风险的多样性等特点，以及具有风险规避、价格发现和资产配置功等功能。股票指数期货交易的实质是投资者将其对整个股票市场价格指数的预期风险转移至期货市场的过程。套利交易在股指期货市场中有着相当重要的意义：一是可以起到稳定价格的作用。价格发现是套利交易重要作用之一，当标的资产价格出现非正常波动时，套利交易者开始进入市场，通过大量的套利交易，引導标的资产回归正常价格轨道。另一方面，套利行为有助于股指期货市场流动性的提高。套利行为的存在不仅增加了股指期货市场的交易量，也增加了股票市场的交易量，起到了市场润滑剂和减震器的作用，有利于减弱市场垄断力量，保证交易者的正常进出和套期保值操作的顺利实现。

本文在统计套利策略基础上，预计设计一种基于GARCH模型的时变方差统计套利策略，并利用沪深300指数与期货的日收盘价格进行实证分析。

1.基于GARCH模型的统计套利理论

T. Bollerslev于1986年提出了GARCH模型，该模型的方差不仅与前q期的随机误差的平方 有关，还与前p期的随机误差的方差 有关，也是解释金融数据中存在的条件异方差的一种处理方式。GARCH（p，q）模型为：

其中，方程式（1）中第一个方程为均值方程，即要估计的回归方程;第二个方程是GARCH模型的核心即方差方程。ut服从GARCH（p，q）的过程，α0>0，α1，γ1≥0。

在进行GARCH模型的统计套利之前我们需要对变量进行平稳性检验，协整检验。平稳性检验是指构成随机过程的随机变量集合{yt}是随着时间t不断变化的变量集合，在随机过程概念中，如果随机过程的变量值不随时间t的变化而变化，即满足下面的关系，这里称这个过程为白噪声过程。

当把以上检验过程完成后，下面开始构建GARCH模型的统计套利过程。在构建统计套利的过程首先需要确定的是对套利区间交易触发信号的确定，所谓的交易信号其实是一个临界值，而临界值就是当这个参数提示某种操作时到达的数值。本文就主要是运用GARCH模型来确定这个临界值套利机会出现在残差序列偏离均值的时候，因为不管残差序列怎样变动，都会回归到平均值，而统计套利策略正是建立这个理论基础之。如果残差恢复到均值，就进行反向操作。当残差偏离均值达到残差标准差的某个倍数时，被认为交易信号出现，那么操作进行，当残差观察到接近均值，反向进行操作指令来获取投资收益。所谓的止损点是指标准差的某个更高的倍数，如果残差偏离均值达到止损点，就意味着损失超过预期止损，这时将套利投资组合进行平仓交易处理。

2.实证分析

2.1数据选取与处理

实证分析的样本数据选择沪深300当月连续期货（IF00.CFE）日收盘价格和沪深300股指现货（000300.SH）日收盘价格，时间区间为2016年4月13日至2018年4月12日，共获得488组样本数据，上述沪深300股指期货与现货分别以Ft 和St表示，并用nt=Ft-St表示基差，                  表示基差的对数收益率。为

了避免伪回归现象，这里借助Eviews软件对沪深300指数基差样本数据日对数收益率做ADF单位根检验，检验结果显示，ADF检验的P值在有限的小数位下均为0，均小于0.05和0.01下的显著水平，即拒绝原假设不存在单位根，因此说明该两列数据是平稳序列，而且均是一阶单整序列。对沪深300指数基差样本数据的日对数收益率进行自相关和偏自相关分析后，可建立常数均值方程，对常数均值方程的残差序列进行ARCH-LM检验，结果F统计量的P值为0，小于0.01下的显著性水平，故拒绝原假设，则存在ARCH效应可建立GARCH（1，1）模型。通过上述分析可以得知，沪深300期货和300指数现货的日收盘价都进行对数化处理，形成了一阶单整形式。本部分对两列数组进行协整检验，用到的方法是Johansen检验法，利用Eviews软件检验后，沪深300期货和300指数现货之间关系是F=1.056·S，即说明现货是期货近1.056倍。

2.2模型构建

鉴于上节的数据描述处理，发现样本数据呈现右偏尖峰后尾分布，为此这里采用t分布对沪深300指数基差样本数据的日对数收益率yt建立GARCH（1，1）模型，以便更准确地刻画数据尖峰后尾特征。由结果可知，GARCH（1，1）模型的均值方程：dt=0.001016+0.707909μt;方差方程：

方差方程中所有系数都是统计显著的，且所有系数均大于 0，标准误差较小，ARCH与GARCH 项系数之和为0.983895<1，t统计量在0.01的显著性水平下显著，这表明建立的GARCH（1，1）过程平稳。下面，对GARCH模型的残差进行滞后5期的ARCH-LM检验，由检验结果可知，F统计量的P值为0.3571，大于0.01下的显著性水平，故接受原假设，则不存在ARCH效应，说明利用GARCH（1，1）模型消除了残差序列的条件异方差性。

至此，基于 GARCH 模型的交易策略已经成型：考虑到存在交易费用及样本外数据的波动，本文以考虑到存在交易费用及样本外数据的波动，本文以σt为统计套利交易的触发线，以±2σ为交易的止损线。其中，我们需要认为设定系数δ1和δ2，本文经过实验比较，最后采取经典文献设定的系数，即δ1=δ2=1。因此，交易策略可以总结如下：

（1）当dt>δ1σt时，买进1.056单位沪深300股指，融券卖空1单位沪深期货。

（2）当dt<-δ2σt，买进1单位的沪深300期货，融券卖空1.056单位沪深300指数。

（3）当dt反向变化直到穿过0时，则平掉当前持有头寸。

3.结论

本文基于GARCH模型进行套利研究。通过构建GARCH模型的套利策略，并对沪深300股指期现货样本数据进行实证分析，发现当dt>δ1σt时，买进1.056单位沪深300股指，融券卖空1单位沪深期货;当dt<-δ2σt，买进1单位的沪深300期货，融券卖空1.056单位沪深300指数;当dt反向变化直到穿过0时，则平掉当前持有头寸。综上所述，通过构建具有较强操作性的股指期货期现套利模型，并以沪深300股指期货真实交易数据为基础进行实证分析，结果表明目前国内股指期货市场存在较多的期现套利机会，市场有效性缺失，故建议逐步放开对基金参与股指期货的诸多限制，充分发挥股指期货市场的套期保值和价格发现功能。

参考文献

[1]Merton R C.Optimum consumption and portfolio rules in a continuous-time model[J].Journal of Economic Theory，1971，3（4）：373-413.

[2]Modest D M，Sundaresan M.The relationship between spot and futures prices in stock index futures markets： Some preliminary evidence[J].Journal of Futures Markets，1983，3（1）：15-41.

[3]Cox J C，Jr J E I， Ross S A.The relation between forward prices and futures prices[J].Journal of Financial Economics，2006，9（4）：321-346.

[4]康敏晨.基于协整和GARCH模型的统计套利策略研究[D].2013.

[5]刘阳，李艳丽，陆贵斌.基于信息更新NN-GARCH模型的统计套利研究[J].統计与决策，2016（02）：169-171.

[6]侯世英，宋良荣，王国俊.基于BP-GARCH模型的统计套利策略[J].统计与决策，2020，36（10）：149-152.

[7]陈其安，张慧，陈抒妤.股指期货交易加剧了中国股票市场波动性吗？——基于投资者结构的理论和实证研究[J].中国管理科学，2020，28（04）：1-13.

作者简介：牛皓淼（1994-），男，山东枣庄人，硕士研究生，研究方向：金融风险管理。