善思辟“蹊径”

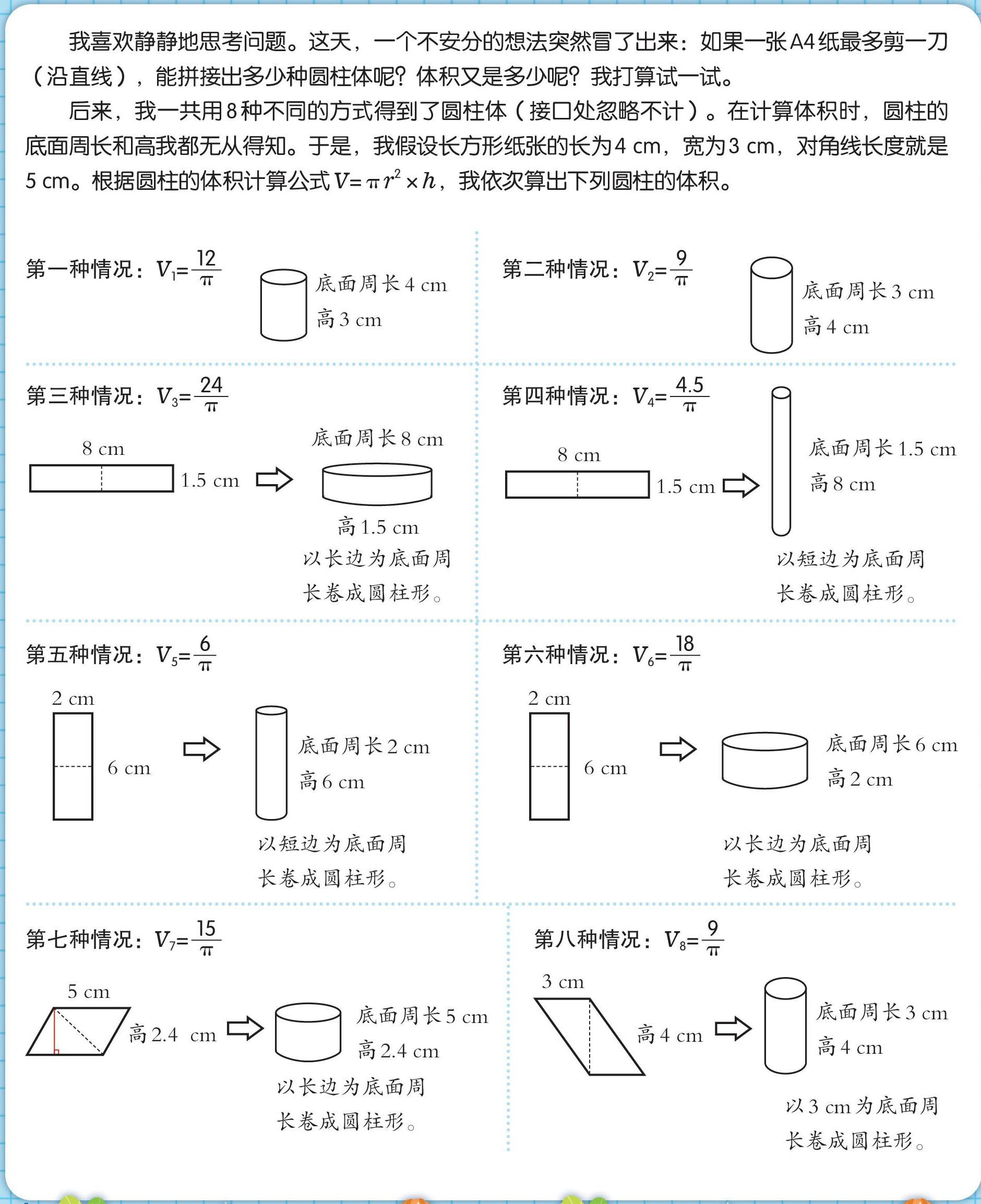
我喜欢静静地思考问题。这天，一个不安分的想法突然冒了出来：如果一张A4纸最多剪一刀（沿直线），能拼接出多少种圆柱体呢？体积又是多少呢？我打算试一试。

后来，我一共用8種不同的方式得到了圆柱体（接口处忽略不计）。在计算体积时，圆柱的底面周长和高我都无从得知。于是，我假设长方形纸张的长为4 cm，宽为3 cm，对角线长度就是5 cm。根据圆柱的体积计算公式V=πr2×h，我依次算出下列圆柱的体积。

我将几种圆柱的底面周长从大到小排序，我发现用长4 cm、宽3 cm的纸做出的圆柱：底面周长越大，圆柱的体积越大;圆柱的高越小，圆柱的体积越大;V2=V8。

上面八种情况的圆柱侧面积都相等，都是12 cm2。

所以我们可以清楚地知道：

用同一张纸做成的圆柱，侧面积相等的情况下，底面周长越大，高的数值越小，则圆柱体积越大，反之亦然。圆柱体积和底面周长、底面半径之间有着明显的倍数关系。

为了证明上面的结论，我遇到了“拦路虎”——多个字母参与的运算。我先假设长方形的长为a，宽为b，侧面积为12 cm2，即ab=12 cm2。a为底面周长，b为高，b=12

a，a=12

b。

则：

V圆柱=πr2×h=π（a

2π）2b=π（a

2π）2×12

a =3a

π

那么，把a=12

b 代入上面的式子，可得V圆柱=3a

π=3×12

b

×1

π =36

πb。

通过推导公式，我也印证了之前发现的规律，好开心呀！

指导老师 郝高峰

李元也  9月2日  12：01：34

看了张旭正这一次的探究活动，我知道了获取知识的两种重要方式：动手实践和理论计算。动手实践可以让我们很直观地发现问题，感受其中奥秘，而理论计算则能让我们在实践的基础上总结规律，验证推论。

杨丽云  9月2日  15：16：31

张旭正虽然改变了题目的要求，却也因此有了一段不一样的学习经历。最让人难忘的应该是他遇到的“拦路虎”。我想，对待任何事情，遇到任何困难，我们都要积极地去面对，有时还需要一股“敢向虎山行”的勇气！

赵宇然  9月2日  16：05：15

我也注意到张旭正在计算各种圆柱体积时，没有将π换算成3.14代入计算过程，这个想法也是很巧妙的。因为π取3.14时运算不够简便，所以他在计算中保留了π，而且这样也不会影响最终的结果与比较，还能避免计算上的麻烦。