图像边缘检测算法的分析与研究
2021-09-10迟慧智田宇
迟慧智,田宇
(工业和信息化部电子第五研究所,广东 广州 511370)
0 引言
随着科技的不断发展和计算机的广泛普及,图像处理技术越来越多地被应用于工业生产和日常生活的各个领域中,而作为其中的重要内容,图像边缘检测技术也成为近些年的研究重点和热点。图像边缘是图像区域属性突变的地方,即有不同灰度属性的区域之间的灰度分割线[1],也是图像中信息最集中的地方,在一定条件下包含原图像的所有信息[2]。因此图像的边缘检测与提取效果优劣,对后续的图像处理至关重要[3]。
目前研究人员提出了许多图像边缘检测的相关算法,这些算法各有优缺点;同时,因为图像本身存在较大的差异,使得各个算法不能对所有的图像实现一样的效果。本文通过比较经典算法、深度学习边缘检测算法和新兴边缘检测等算法,分析了这些算法的优缺点和适用范围,并探讨了边缘检测算法在图像处理领域的新进展和新应用。
1 经典边缘检测算法
经典边缘检测算法可分为一阶微分算子(Roberts 算子、Sobel 算子、Prewitt 算子和Kirsch算子等)和二阶微分算子(Laplacian 算子、LoG算子和Canny 算子等)。其中,一阶微分算子中的Sobel 算子、Prewitt 算子和Kirsch 算子是以Roberts算子为基础发展而来的。
Roberts 算子通过对角线方向相邻两像素之差近似梯度幅值检测边缘,是一种利用局部差分算子寻找边缘的算子,其卷积模板为:
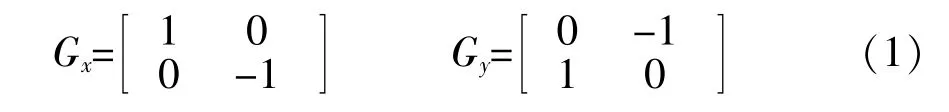
该算子以相邻像素之差近似梯度,计算公式如下所示:

梯度大小用像素强度表示,梯度幅值计算为:
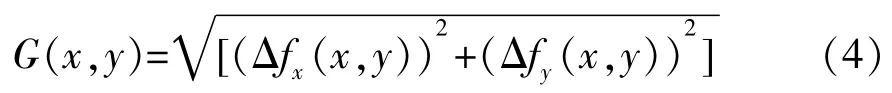
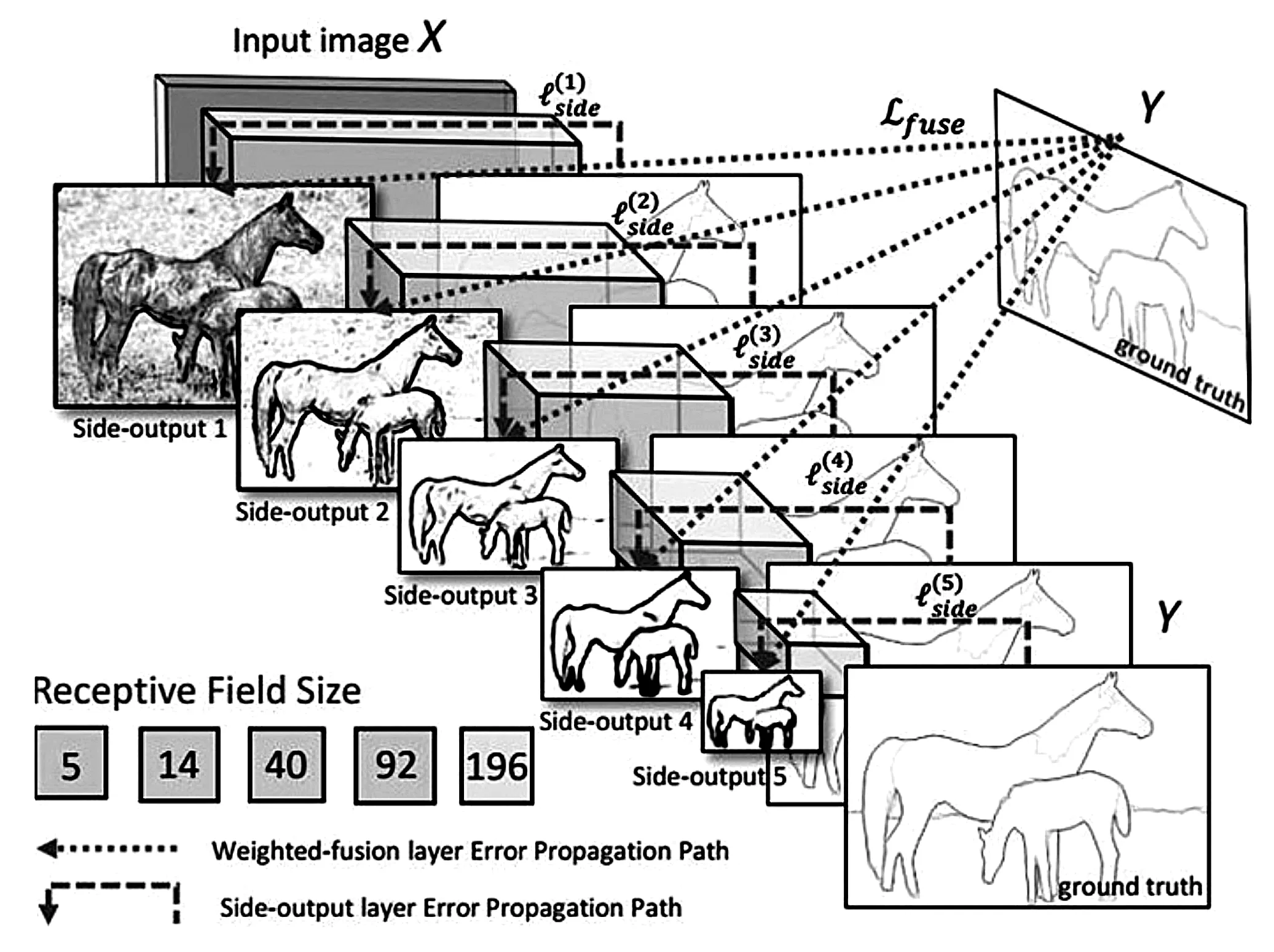
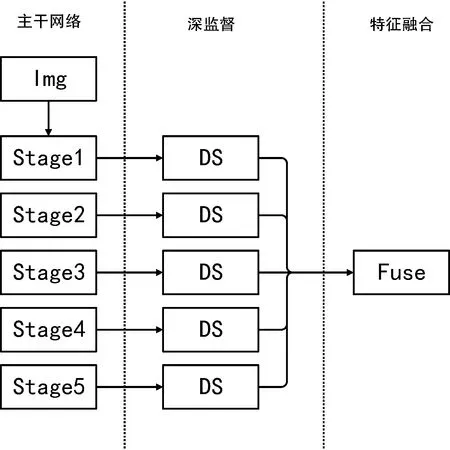
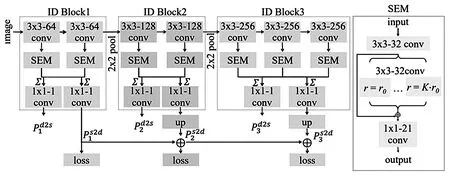
图像边缘与梯度方向垂直[4],当阈值Th Sobel 算子和Prewitt 算子在Roberts 算子的基础上,采用改进的3◇3 卷积模板,如下所述。 a)Sobel 算子卷积模板 b)Prewitt 算子卷积模板 Sobel 算子利用这两个横向纵向模板对图像做平面卷积,得到图像亮度的灰度差近似值。由于采用了方形差分和局部平均的加权平均算法,Sobel算子对噪声有平滑作用,但也因此导致边缘定位精度不高的问题[6],如图1d 所示。Prewitt 算子通过式(6)的卷积模板对图像进行邻域卷积实现边缘检测,两个方向模板一个检测图像的水平边缘,一个检测图像的垂直边缘。经典Prewitt 算子使用平均差分计算梯度,类似于低通滤波,对噪声有一定的抑制效果,但这也导致图像边缘定位精度不足,如图1c 所示。 图1 一阶微分算子边缘检测效果对比图 二阶微分算子中,Canny 算子在各种边缘检测中表现出良好的性能,并且形成了完整的最优检测算法的标准。经典Canny 算子的边缘检测步骤[7]如下所述。 a)利用高斯滤波器对原图像滤波降噪。 b)利用梯度算子计算4 个方向(0°,45°,90°,135°)的梯度幅值和方向,通常利用一阶微分算子作为模板计算(Roberts、Prewitt 和Sobel)算子,计算水平和垂直方向的差分Gx和Gy;再利用如下公式计算得到梯度强度G和方向θ: c)进行梯度的非极大值抑制,利用梯度方向的极大值点的保留实现通过梯度幅值图像获取的宽边缘的细化。 d)进行双阈值检测和边缘连接。通常的边缘提取算法只利用一个阈值进行噪声过滤,Canny 算子利用高低阈值进行边缘像素的区分,如果像素点梯度大于高阈值则为强边缘点,小于低阈值则设置灰度为0,在高低阈值之间的则视为弱边缘;利用强边缘断点搜索连接弱边缘并提取出完整边缘。 相较于其他边缘检测算子,Canny 算子检测的边缘连贯细腻,具有良好的检测精度(如图2b 所示),但对光源噪声敏感,且阈值为自定义设置,易导致边缘检测的不稳定。 Laplacian 算子边缘检测常用的卷积模板如下: 作为二阶微分算子,Laplacian 算子天生对噪声敏感,抗噪能力差。从图2c中可以看出,Laplacian 算子很难分辨出清晰的边缘。因此Laplacian 算子通常不用于边缘检测而是边缘定位或锐化。 针对Laplacian 算子出现的问题,Marr 提出了LoG(Laplacian of Gaussian)算子,将高斯低通滤波与Laplacian 算子相结合,对图像先进行高斯滤波,再运用Laplacian 算子进行检测。如图2d 所示,相较于利用Laplacian 算子边缘检测得到的图像,LoG 算子对图像边缘的连续有了较大的改善,但滤波器对图像滤波易丢失部分图像边缘,降低边缘检测精度[8]。 图2 二阶微分算子边缘检测效果对比图 随着人工智能在全球兴起,作为实现手段之一的深度学习也成为了科研人员的研究热点。由于边缘提取场景越来越复杂,图像的纹理或背景对这些利用低层次特征检测边缘的经典边缘检测方法产生了许多干扰,国内外诸多学者尝试在图像边缘检测领域加入深度学习高层次语义应对复杂场景。深度学习可分为两大类:全监督学习和弱监督学习。全监督学习利用已知期望的样本对算法模型进行训练,通过训练期间参数的不断调整,得到最优参数模型,再利用该模型对图像的所有输入作为输出进行相应的判断,最终得到整个图像的边缘。全监督学习中研究较多的有整体嵌套边缘检测(HED:Holistically -Nested Edge Detection),如 RCF:(Richer Convolutional Features for edge dectction)、CASENet(Category-Aware Semantic Edge Detection)和BSDN(Bifurcated Deep Network)等。 HED 是2015 年由XIE[9]提出的一种新的边缘检测算法,其特点是整体图像的训练和预测及多维度的特征学习,利用全卷积神经网络和深监督学习网络自动学习层次表示,HED 的网络整体结构图如图3 所示。从图3中可以看出,HED 在卷积层后插入了带有深度监督的侧输入层,侧输入层实现边缘预测。HED 网络适用于对比度强的图片场景,对比度较弱时图片中其他因素的干扰较大,效果较差。 图3 HED 网络整体结构图 RCF 算法是LIU[10]等在2017 年提出的、以HED 算法为基础的边缘检测算法,同样实现了端到端的边缘检测。RCF 主要结构图如图4 所示,从图4中可以看出,其主体结构分为三大部分:主干网络、深监督和特征融合。RCF 在HED 算法的基础上对每一个stage 都进行深监督学习使其尽快地收敛并得到一张边缘图,利用特征融合模块对5张边缘图进行融合并输出最终结果。由于融合了主干网络的每一层特征,RCF 网络得到的边缘图效果要优于只利用了部分特征的HED 网络。 图4 RCF 网络整体结构 CASENet 在2017 年被YU[11]等人首次提出,CASENet 作为类别感知的语义边缘检测算法,相对于传统的边缘检测的二元问题,将每个边缘像素与至少两个边缘类别相关联,是更为复杂的多元问题。CASENet 是一种新的基于ResNet 的端到端深度语义边缘学习架构,同时也是跳层架构,网络架构如图5 所示。 从图5中可以看出,CASENet 架构相对于DSN 做了一些改进: 1)特征提取模块(图5c 的feature extraction)取代底部的分类模块(图5b 的classification); 2)分类模块(图5c 的classification)置于顶部并进行监督; 3)执行共享级联(图5h)取代切片联接(图5g)。 图5 CASENet 架构图 通常CASENet 被认为是联合边缘检测和分类的网络,它让较低级的特征参与并通过跳层结构增强高级的语义分类。 2019 年HE[12]等首次提出BDCN(Bi-Directional Cascade Network),其网络架构图如图6 所示。从图6中可以看出,BDCN 通过ID block 层利用不同的权重具有双向级联的不同监督取代所有的CNN 输出相同的监督进行学习,同时引入尺度增强模块(SEM:Scale Enhancement Module)以生成多尺度特征。通过BDCN 和SEM 的结合,该方法的ODS 达到了0.828,效果甚至优于人类感知。 图6 BDCN 网络架构图 除了上述经典图像边缘检测算法和新兴的深度学习图像边缘检测算法,还有小波变换算法、数学形态学算法、模拟退火算法、蚁群算法和遗传算法等等,在图像边缘检测中均有大量的研究,这里不再赘述。 在生产生活中,图像边缘检测是众多图像领域任务实施的基础,对于图像边缘检测各国科研人员也做了大量的研究,从边缘检测研究的历史和现状可以看出有以下几个发展趋势: 1)在进行边缘检测前对图像进行更有效的预处理,在去除噪音的同时更大程度地保留原图像要素; 2)在原有的算法上进行优化,一方面对算法本身进行优化,如Canny 算子的双阈值的自适应选取,另一方面结合多个不同的算法,将不同算法的优点结合; 3)特殊图像或复杂图像的边缘检测得到了广泛的关注,边缘检测的要求逐渐地提高,以卷积神经网络为基础的深度学习算法越来越多地应用其中。 本文对图像边缘检测中的经典算法、深度学习算法进行了分析研究,论述了不同算法的原理及优缺点。随着图形处理和自动化检测的快速发展,改进的经典边缘检测算法和深度学习边缘检测算法将成为研究热点。特别是在复杂场景下,图像边缘定位准确,算法响应时间短,抗噪能力强的算法将是一个重要的研究方向。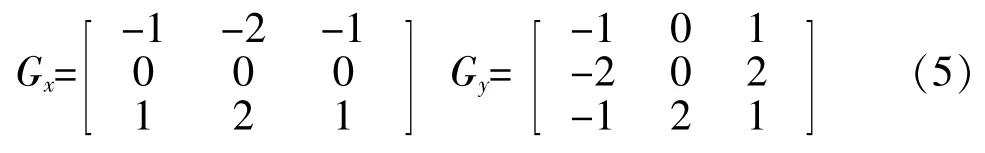
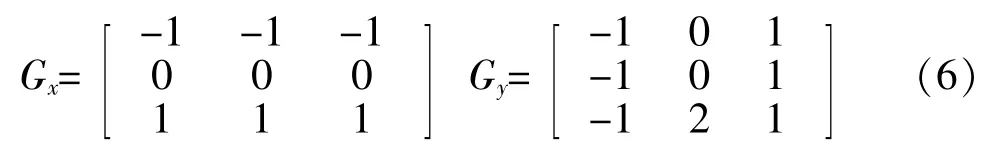


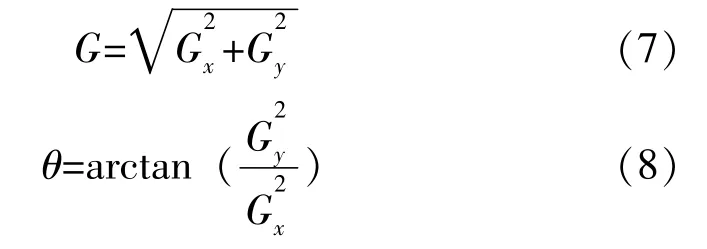



2 新兴边缘检测算法

3 其他边缘提取算法
4 展望
5 结束语
