网型防爆墙防护效果数值模拟

张晓聪

(广州大学 土木工程学院, 广东 广州 510006)

防爆墙通常设置在目标建筑物的周围，用来为其后方区域的建筑物、人员提供一定的安全防护.作为一种被动防护措施，防爆墙从两方面来减弱作用在建筑物上的爆炸荷载：①防爆墙可以阻挡恐怖分子接近目标建筑物，从而提供了一定的防护距离；②防爆墙通过改变爆炸波的传播路径，使爆炸波的能量得到分散，从而降低了目标建筑物上的爆炸波能量输入[1-2].此外，由于建造相对容易，防爆墙在军用和民用领域均得到了大规模应用.因此，不断改进防爆墙的设计，使其达到安全性、经济性以及美观性的统一，就显得十分必要.

世界各国的学者和工程技术人员开发了各种形式的防爆墙，这些防爆墙按原理可分为实体防爆墙、牺牲层结构以及新型防爆墙3类.其中，实体防爆墙[3]利用其结构的刚性将一部分爆炸波的能量反射回去，牺牲层结构[4-5]利用其柔性来吸收爆炸波能量，而新型防爆墙[6-11]则利用爆炸波本身的传播特性以及结构与爆炸波的复杂相互作用(不局限于爆炸波的反射和能量吸收)，比如通过不同爆炸波之间的相互作用来实现波能自消耗.

Zong等[8]基于波能自消耗的概念，提出了由一排护栏柱构成的护栏型防爆墙设计，通过相邻护栏柱绕射波之间的相互作用，在墙后区域发生爆炸波能量的自消耗，从而为墙后人员和建筑物提供防护.通过开展二维的数值模拟，证明了护栏型防爆墙在减小墙后爆炸荷载的有效性.

侯帅波[10]提出了在护栏柱前方增加横杆的网型防爆墙设计，并通过数值模拟证明了网型防爆墙的防护有效性和安全性，但是未对网型防爆墙的衰减机理作深入分析.此外，该研究中横杆和纵杆的直径取值为100 mm，这与网型防爆墙在实际应用时有较大差距.因此，本研究中的横杆、纵杆全部采用圆形截面，并以20 mm为基本直径尺寸，以最大程度接近实际应用场景.

本文比较了网型防爆墙与护栏型防爆墙在同一工况下的爆炸荷载衰减率，从而对网型防爆墙的防护效果作出评价，并对其防护原理进行了分析.

1 数值模型的建立

1.1 计算方法介绍

在数值模拟中，通过对比墙后各个测点的超压峰值与冲量，来研究墙后区域爆炸荷载的分布，从而对防爆墙的防护有效性作出评估.典型的测点超压时程曲线如图1所示.

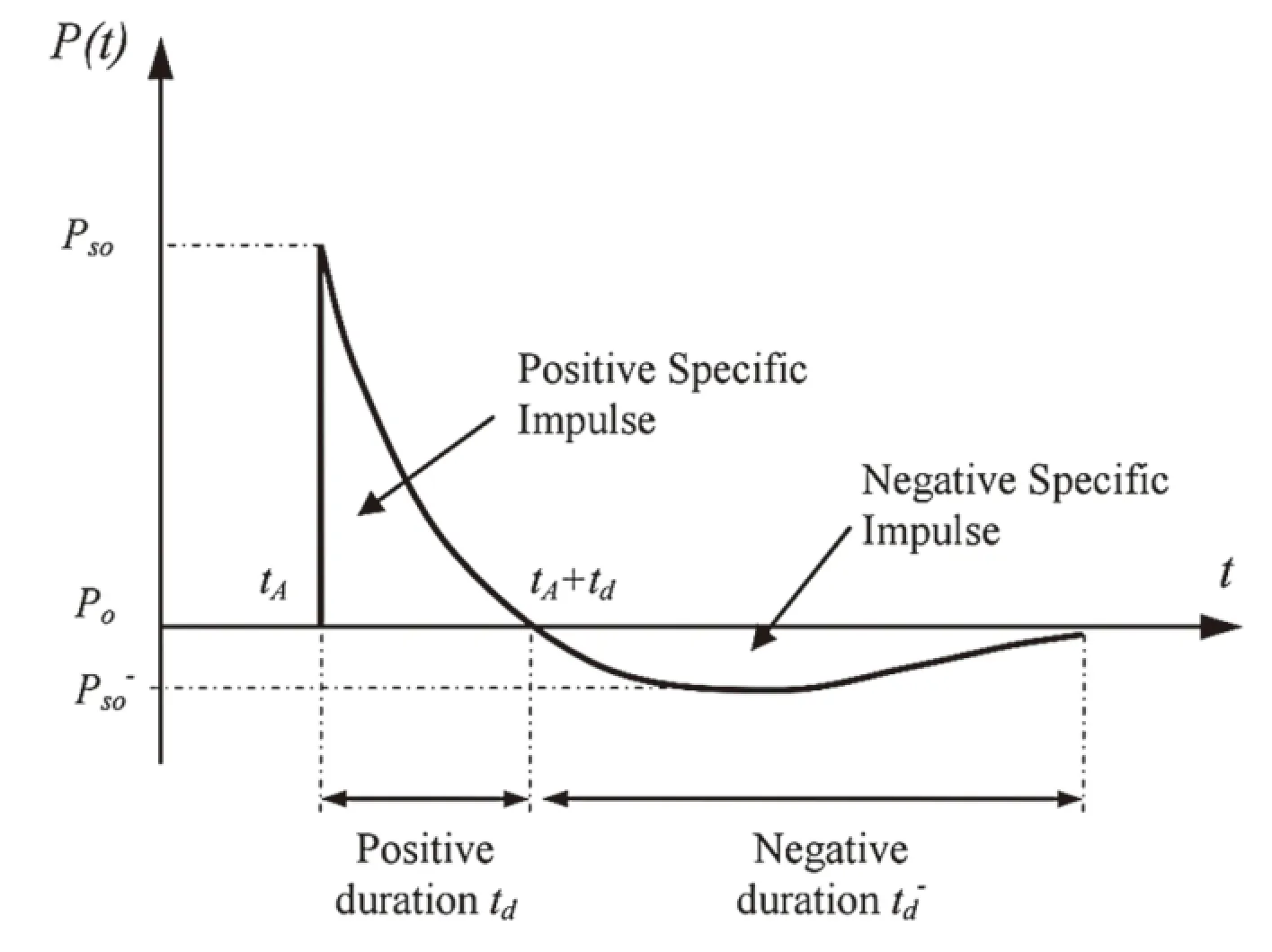
图1 典型的测点超压时程曲线[12]Fig.1 Typical blast pressure profile of gauges

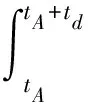
采用LS-DYNA软件的LBE/ALE方法进行数值模拟，其计算过程分为两个阶段：①利用Kingery[13]的经验公式，计算出空气域前表面的爆炸超压分布；②以前一阶段的计算结果为初始条件，利用ALE单元模型的多物质选项，对爆炸波在空气中的传播、结构与爆炸波的相互作用进行模拟.因此，LBE/ALE方法只需要对结构周围一定范围内的空气进行建模，从而使计算量明显减小.在LBE/ALE模型中，空气域模型的前表面被定义为周围层(Ambient layer)，从而可以接收经验公式法计算得到的爆炸超压分布.

利用流固耦合算法(关键字*CONSTRAINED_LAGRANGE_IN_SOLID)，可以对结构与爆炸波的相互作用进行建模，从而模拟爆炸波的反射、绕射、透射以及能量吸收现象.流固耦合算法利用ALE空气单元计算出结构所受的作用力，与此同时，结构为爆炸波的传播提供了约束条件.

1.2 模型参数的确定

图2为计算模型示意图.取1.0 kg TNT炸药地面起爆的工况进行分析.空气域的长度、宽度和高度分别为3.1 m、4.0 m和2.0 m.由于模型的对称性，只需建立1/2宽度，即2.0 m宽的空气域模型即可.防爆墙的宽度为4.0 m，高度为1.0 m，与炸药中心的距离均为1.25 m.在防爆墙后方0.25 m、0.75 m、1.25 m、1.75 m及2.25 m分别布置了5个测点，测点高度均为0.25 m.为便于描述测点的位置，引入无量纲量D/H，其中，D为测点的墙后距离，H为防爆墙的高度，5个测点对应D/H分别为0.25、0.75、1.25、1.75和2.25，并用T1-T5代表防爆墙后的5个测点.模型的下表面设为固定边界，以模拟地面对爆炸波的反射现象；由模型的对称性，右表面应设为对称边界；上表面、后表面、左表面均设为无反射边界，以达到模拟无限大空气域的效果.由于结构的刚度对爆炸荷载的计算结果影响不大[14]，因此，将防爆墙视为刚体，从而简化计算.

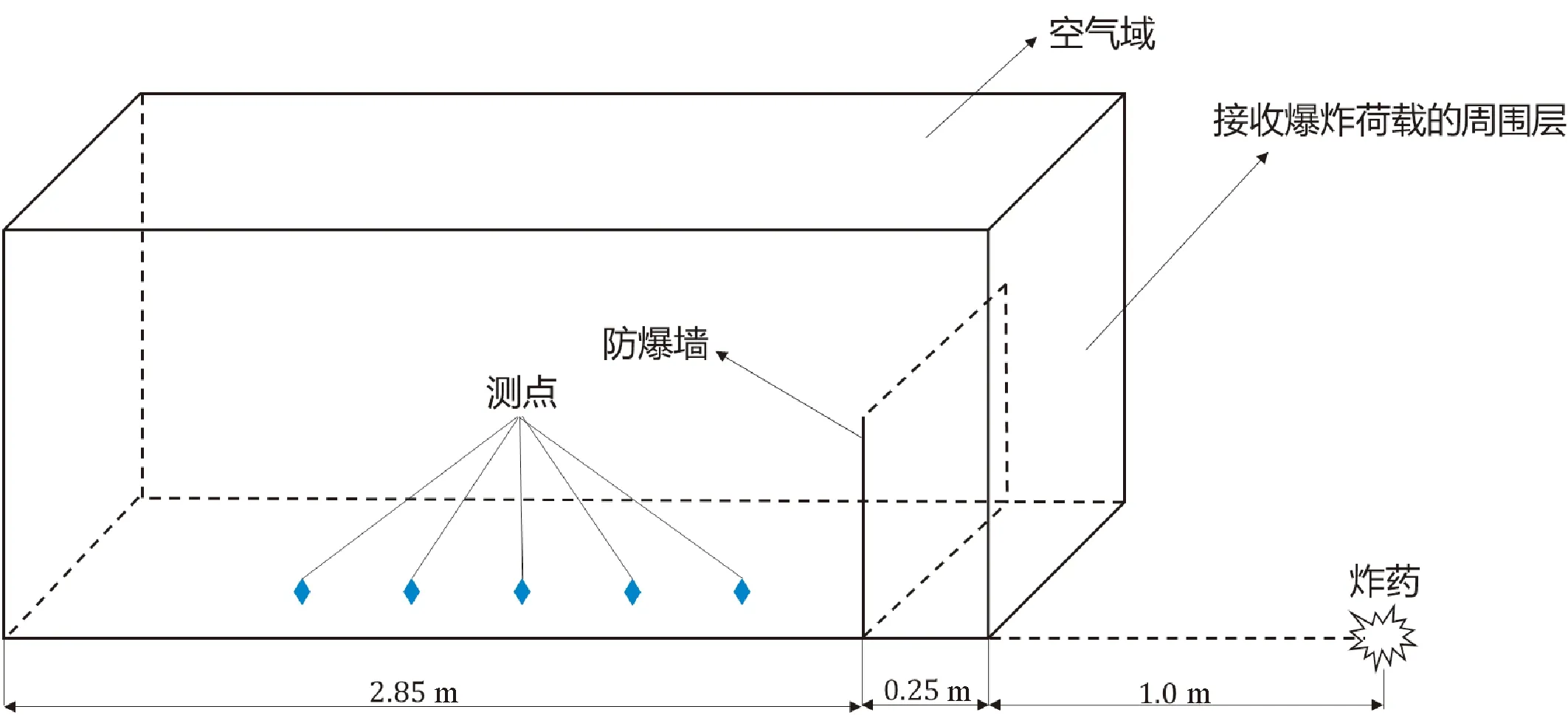
图2 计算模型示意图Fig.2 Sketch of numerical model

在本文的模型中，防爆墙的宽度为4.0 m，高度为1.0 m，与炸药中心的距离均为1.25 m.综合考虑护栏的防护效果与自身所承受的净爆炸荷载[8, 15]，以及在城市地区应用的实际情况，将护栏的截面形状确定为圆形.

空气采用理想气体模型，其材料模型通过关键字*MAT_NULL定义，状态方程通过关键字*EOS_LINEAR_POLYNOMIAL定义，空气单元的压强表达式如(1)所示：

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)e

(1)

式中，μ=ρ/ρ0-1，其中,ρ和ρ0分别为空气在当前时刻和初始时刻的密度；e为单位体积空气的内能；常数C0=C1=C2=C3=C6=0，C4=C5=γ-1，其中，绝热指数γ=1.4.将空气单元的初始压强设为101.325 kPa，密度设为1.225 kg/m3，以模拟平均海平面的海拔高度以及15 ℃温度条件的标准工况.

1.3 网格收敛性测试

为确定合理的网格尺寸，比较了3种不同的空气网格尺寸，即60 mm、30 mm以及15 mm在自由空气场的工况下的计算结果，见图3.取1.0 kg TNT炸药地面起爆的工况进行分析.空气域的长度、宽度、高度分别为3.1 m、4.0 m和2.0 m.由于模型的对称性，只需建立1/2宽度，即2.0 m宽的空气域模型即可.在距离炸药中心1.5 m、2.0 m、2.5 m、3.0 m及3.5 m处布置了5个测点，且测点高度均为0.25 m.模型的下表面设为固定边界，以模拟地面对爆炸波的反射现象；由模型的对称性，右表面应设为对称边界；上表面、后表面和左表面均设为无反射边界，以达到模拟无限大空气域的效果.从图 3可以看出，空气网格尺寸的变化对冲量值的影响不明显，冲量在30 mm网格时就已收敛.而超压峰值对网格尺寸的变化较为敏感.由于计算机的性能有限，选取15 mm为空气网格尺寸.

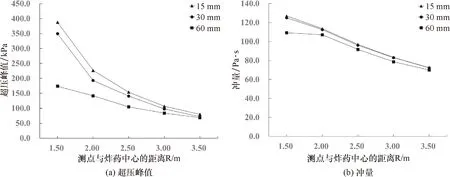
图3 网格收敛性测试结果Fig.3 Mesh convergence test results

1.4 模型验证

通过单层圆形护栏柱的现场试验结果[7]，来验证数值模型的正确性.按照该试验的布置方案(图4)，取1.0 kg TNT炸药地面起爆的工况进行分析，空气域的长度、宽度、高度分别为3.1 m、6.0 m和2.0 m.由于模型的对称性，只需建立1/2宽度，即3.0 m宽的空气域模型即可.防爆墙的宽度为6.0 m，高度为1.0 m，与炸药中心的距离为1.25 m.所有护栏柱的直径均为20 mm，柱间净距为10 mm.模型的下表面设为固定边界，以模拟地面对爆炸波的反射现象；由模型的对称性，右表面应设为对称边界；上表面、后表面、左表面均设为无反射边界，以达到模拟无限大空气域的效果.由于结构的刚度对爆炸荷载的计算结果影响不大[14]，因此将防爆墙视为刚体，从而简化计算.分别选取墙后距离为0.8 m、1.8 m和2.8 m的3个测点，测点的超压峰值与冲量的对比结果如图 5所示.从图5可以看出，测点的冲量结果与试验结果吻合较好，超压峰值虽与试验结果相比偏低，但3个测点的误差均在11.5%以下，从而证明了模型在预测墙后爆炸荷载方面的准确性.

图4 单层圆形护栏柱的现场试验[7]

图5 模型验证结果Fig.5 Model validation results

2 计算结果

在1.0 kg TNT炸药地面起爆的工况下，比较了网型防爆墙与护栏型防爆墙对墙后爆炸荷载的衰减比例，从而对网型防爆墙的防护效果做出评价，同时对其防护原理进行分析.空气域的长度、宽度、高度分别为3.1 m、4.0 m和2.0 m.由于模型的对称性，只需建立1/2宽度，即2.0 m宽的空气域模型即可.防爆墙的宽度为4.0 m，高度为1.0 m，与炸药中心的距离均为1.25 m.在防爆墙后方0.25 m、0.75 m、1.25 m、1.75 m及2.25 m分别布置了5个测点，测点高度均为0.25 m.为了便于描述测点的位置，引入无量纲量D/H，其中，D为测点的墙后距离，H为防爆墙的高度，5个测点分别对应D/H为0.25、0.75、1.25、1.75、2.25，并用T1-T5代表防爆墙后的5个测点.模型的下表面设为固定边界，以模拟地面对爆炸波的反射现象；由模型的对称性，右表面应设为对称边界；上表面、后表面、左表面均设为无反射边界，以达到模拟无限大空气域的效果.其中，护栏型防爆墙的纵杆直径为20 mm，杆间净距为10 mm(相对空隙率ROF=33%).对护栏型防爆墙和网型防爆墙而言，由于相对空隙率对其防护效果起着决定性作用[16]，同时考虑实际施工的简便，将网型防爆墙的横、纵杆间距比设为1.为保证对比的公平性，网型防爆墙的用钢量、相对空隙率均与护栏型防爆墙保持一致，经过计算确定其纵杆与横杆的直径均为15.8 mm，纵杆间距与横杆间距均为21.6 mm，如图6所示.

图6 护栏型防爆墙与网型防爆墙的模型示意图Fig.6 Configuration of fence blast wall and net blast wall

2.1 网型防爆墙与护栏型防爆墙的防护效果对比

图7和图8分别给出了网型防爆墙与护栏型防爆墙的墙后爆炸荷载对比结果.从图7、8可以看出：①与自由空气场工况相比，网型防爆墙与护栏型防爆墙对其后方区域的爆炸荷载均有一定程度的削弱；②网型防爆墙对墙后测点超压峰值的衰减效果优于护栏型防爆墙，但是这一优势随着D/H的增大而逐渐减弱；③整体而言，网型防爆墙对墙后测点冲量值的衰减效果不如护栏型防爆墙.当D/H=0.25时，网型防爆墙后方测点的冲量低于护栏型防爆墙；当D/H=0.75时，网型防爆墙后方测点的冲量与护栏型防爆墙相差不大；当D/H≥1.25时，网型防爆墙后方测点的冲量反而高于护栏型防爆墙.

图7 网型防爆墙与护栏型防爆墙的墙后爆炸荷载对比结果Fig.7 Comparison of peak reflected overpressure and impulse on fence blast wall and net blast wall

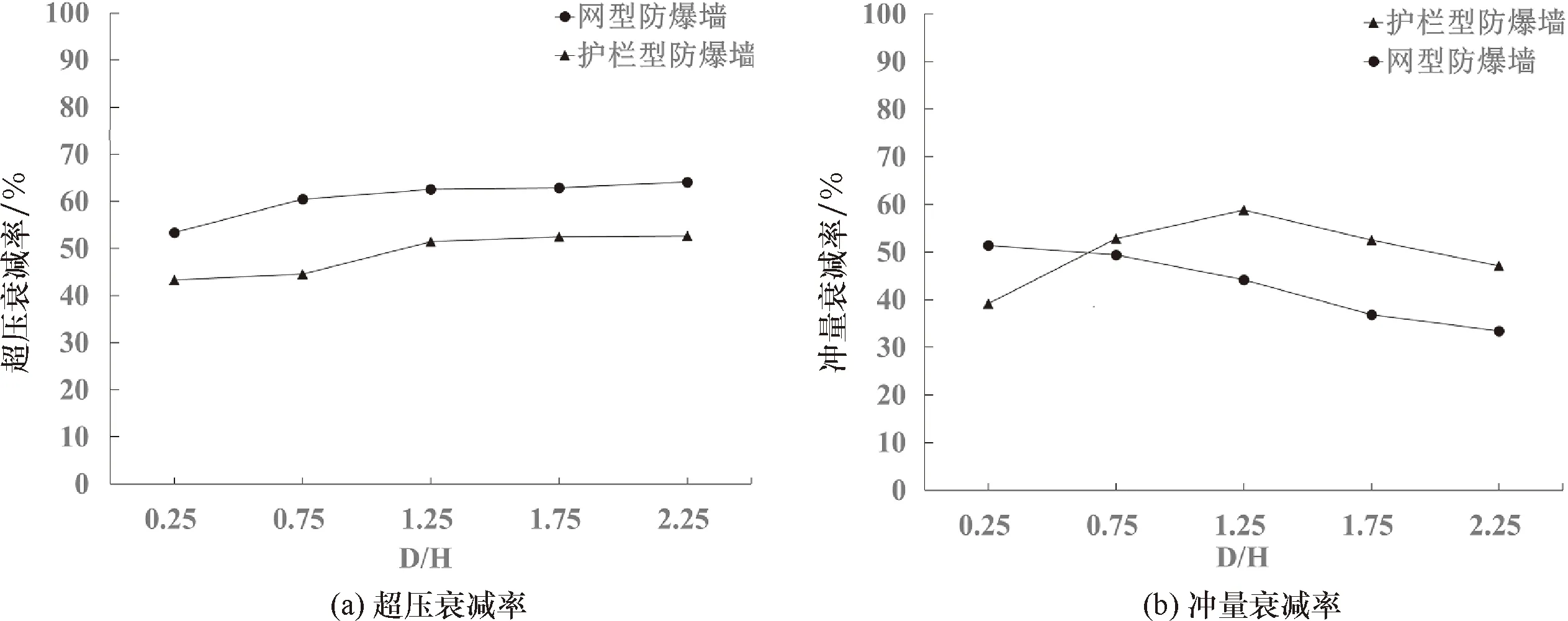
图8 网型防爆墙与护栏型防爆墙的墙后爆炸荷载衰减率对比结果Fig.8 Comparison of blast load reduction on fence blast wall and net blast wall

2.2 超压时程曲线分析

图9给出了护栏型防爆墙在测点T1、T2处的超压时程曲线.从图9可以看出，护栏型防爆墙在墙后测点T1和T2处的超压时程曲线接近于单峰.这说明，护栏型防爆墙在这两个测点处的超压主要由透射波组成，即阴影效应占主导.

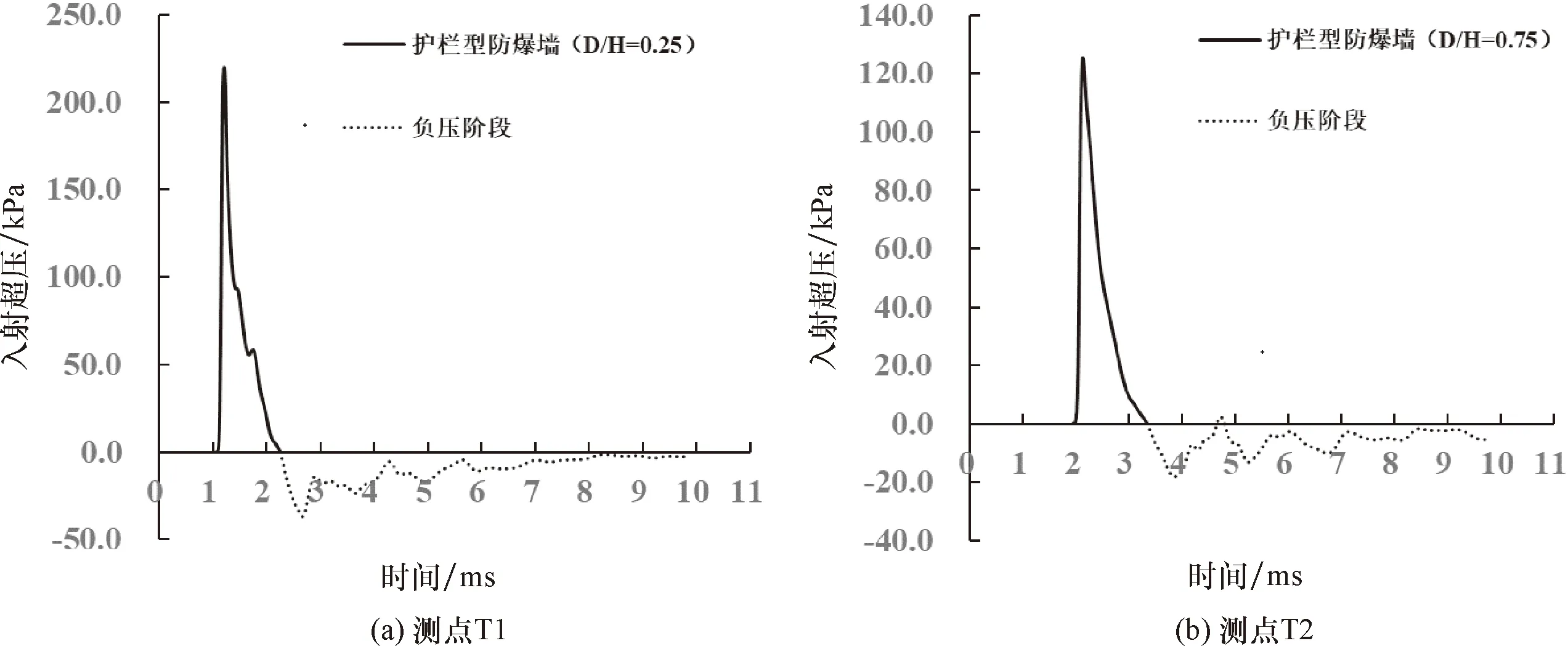
图9 护栏型防爆墙在测点T1、T2处的超压时程曲线Fig.9 Overpressure-time histories at T1-T2 of fence blast wall

图10给出了护栏型防爆墙在测点T3、T4及T5处的超压时程曲线.从图10可以看出，虽然护栏型防爆墙在测点T3、T4和T5处的超压时程曲线出现了双峰或多峰现象，但是对这些测点的爆炸荷载影响不大.这是因为：①测点的第二个超压峰值明显低于第一个超压峰值，因此对测点的超压峰值没有影响；②测点第二次出现正相超压是在测点经历了一段负压之后，加上该正压的峰值较小，因此对冲量的影响不明显.

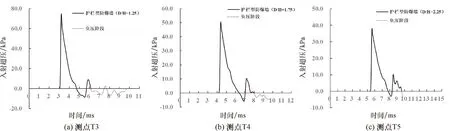
图10 护栏型防爆墙在测点T3、T4、T5处的超压时程曲线Fig.10 Overpressure-time histories at T3-T5 of fence blast wall

图11给出了网型防爆墙在墙后测点T1处的超压时程曲线.从图11可以看出，网型防爆墙在测点T1处已有一定的叠加效应.但是，由于测点第二次出现的正相超压峰值较小，因此对测点的超压峰值没有影响，且对测点冲量值的影响较为有限.换言之，网型防爆墙在测点T1处的爆炸荷载仍主要由透射波所决定，即测点T1仍属于由阴影效应占主导的阴影区域.

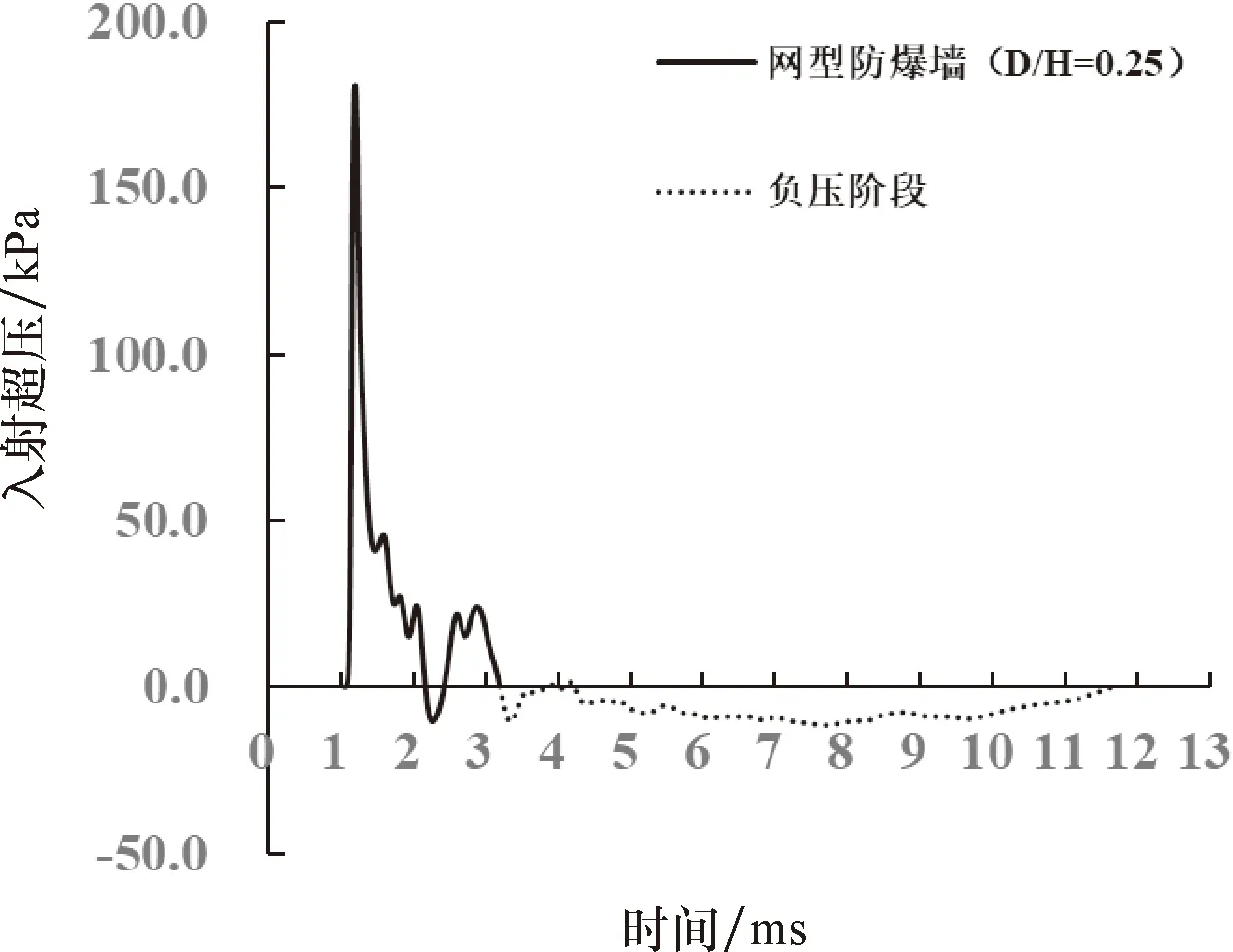
图11 网型防爆墙在墙后测点T1处的超压时程曲线Fig.11 Overpressure-time histories at T1 of net blast wall

图12给出了网型防爆墙在墙后测点T2、T3、T4和T5处的超压时程曲线.从图12可以看出，网型防爆墙在测点这几处的叠加效应较为显著，且随着D/H的增大，在第一个超压峰值之后出现的正相超压对测点的爆炸荷载影响较为明显.这说明，随着D/H的增大，阴影效应对网型防爆墙后方测点爆炸荷载的影响逐渐减弱，而叠加效应逐渐增强，并占据主导地位.

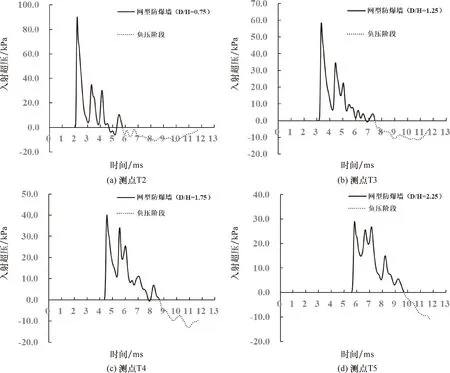
图12 网型防爆墙在墙后测点T2、T3、T4、T5处的超压时程曲线Fig.12 Overpressure-time histories at T2-T5 of net blast wall

2.3 超压峰值分析

图13和图14分别给出了护栏型防爆墙和网型防爆墙各测点取得超压峰值时的压强云图.从图13、14可以看出，无论是护栏型防爆墙，还是网型防爆墙，其墙后测点的超压第一次达到峰值(也是测点最终的超压峰值)的时刻都恰好是透射波到达相应测点的时刻.这说明，对于护栏型防爆墙与网型防爆墙来说，墙后测点的超压峰值仅取决于透射波，而由于透射波的强度主要取决于阴影效应，因此，墙后测点的超压峰值主要由阴影效应的显著程度决定.

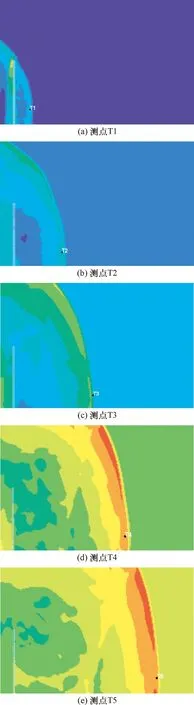
图13 护栏型防爆墙各测点达到超压峰值时的压强云图Fig.13 Pressure contour of gauges behind the fence blast wall

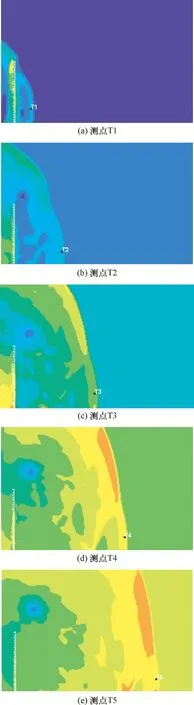
图14 网型防爆墙各测点达到超压峰值时的压强云图Fig.14 Pressure contour of gauges behind the net blast wall

虽然网型防爆墙与护栏型防爆墙的用钢量、相对空隙率均保持一致，但是从二者墙后测点的超压峰值结果(图7)可以看出，网型防爆墙的阴影效应比护栏型防爆墙更加显著.这可能是由于虽然二者对爆炸波的反射面积相等，但由于地面起爆的工况使得防爆墙前表面的爆炸荷载并不是均匀分布的，而是越靠近地面的爆炸荷载越大，从而导致对于这两种防爆墙而言，反射表面越靠近地面，其对爆炸波的反射作用越显著.

通过观察网型防爆墙与护栏型防爆墙的反射面积分布(图6)可以看出，虽然反射表面的总面积相等，但由于网型防爆墙靠近地面的反射面积所占比例更大，因此，即使在用钢量、相对空隙率均保持一致的情况下，网型防爆墙对爆炸波的反射效果依然优于护栏型防爆墙，即网型防爆墙后方的阴影效应比护栏型防爆墙更加显著，从而导致网型防爆墙在所有测点处的超压峰值均低于护栏型防爆墙.

2.4 冲量分析

图15给出了网型防爆墙与护栏型防爆墙在测点T1处的超压时程曲线对比结果.从图15可以看出，与护栏型防爆墙相比，虽然网型防爆墙测点的超压持续时间更长，但由于网型防爆墙测点的超压峰值更低，而且随后出现的正相超压对测点的总冲量值影响有限，从而导致网型防爆墙在测点T1处的冲量值低于护栏型防爆墙.

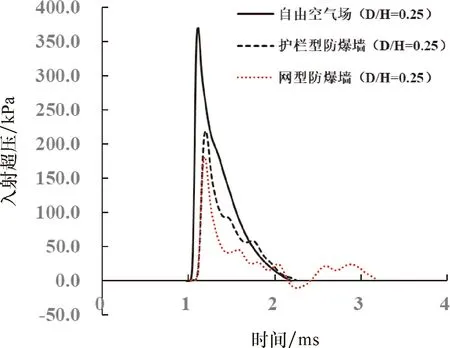
图15 网型防爆墙与护栏型防爆墙在测点T1处的超压时程曲线对比结果

图16给出了网型防爆墙与护栏型防爆墙在测点T2处的超压时程曲线对比结果.从图16可以看出：①与护栏型防爆墙相比，网型防爆墙在测点T2处的正压持续时间更长；②网型防爆墙后方测点T2的超压峰值低于护栏型防爆墙.这两方面因素共同作用，使得两种防爆墙在测点T2处的冲量结果相差不大.

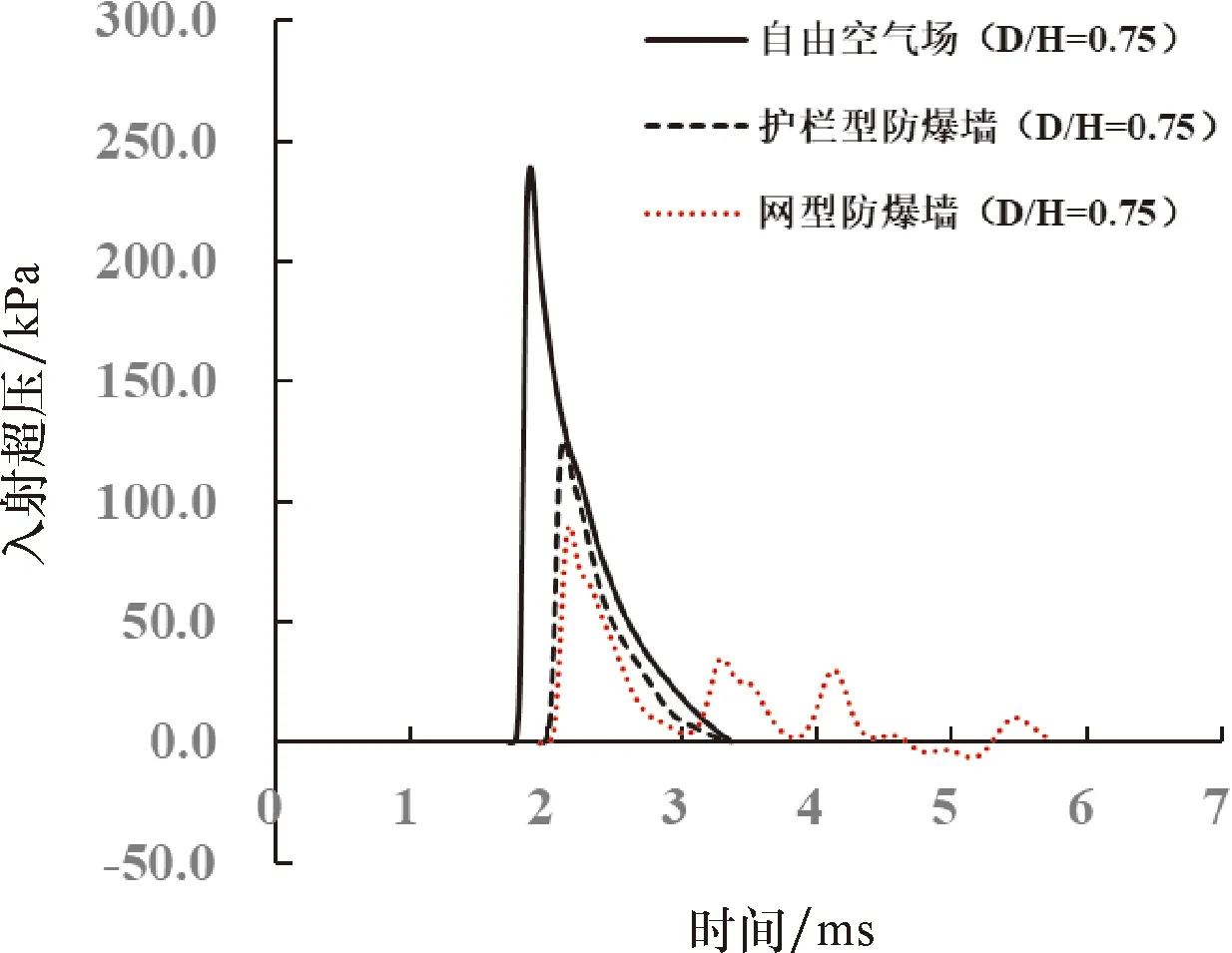
图16 网型防爆墙与护栏型防爆墙在测点T2处的超压时程曲线对比结果

图17给出了网型防爆墙与护栏型防爆墙在测点T3、T4、T5处的超压时程曲线对比结果.从图17可以看出，对网型防爆墙而言，当D/H≥1.25时，由于随后出现的多个超压峰值与第一个超压峰值越来越接近，其对测点冲量值的影响较为显著，从而导致网型防爆墙的叠加效应越来越明显；而护栏型防爆墙在D/H≥1.25的测点处超压时程曲线接近于单峰，仍由阴影效应占主导，而叠加效应不明显.因此，当D/H≥1.25时，网型防爆墙的冲量值反而大于护栏型防爆墙.

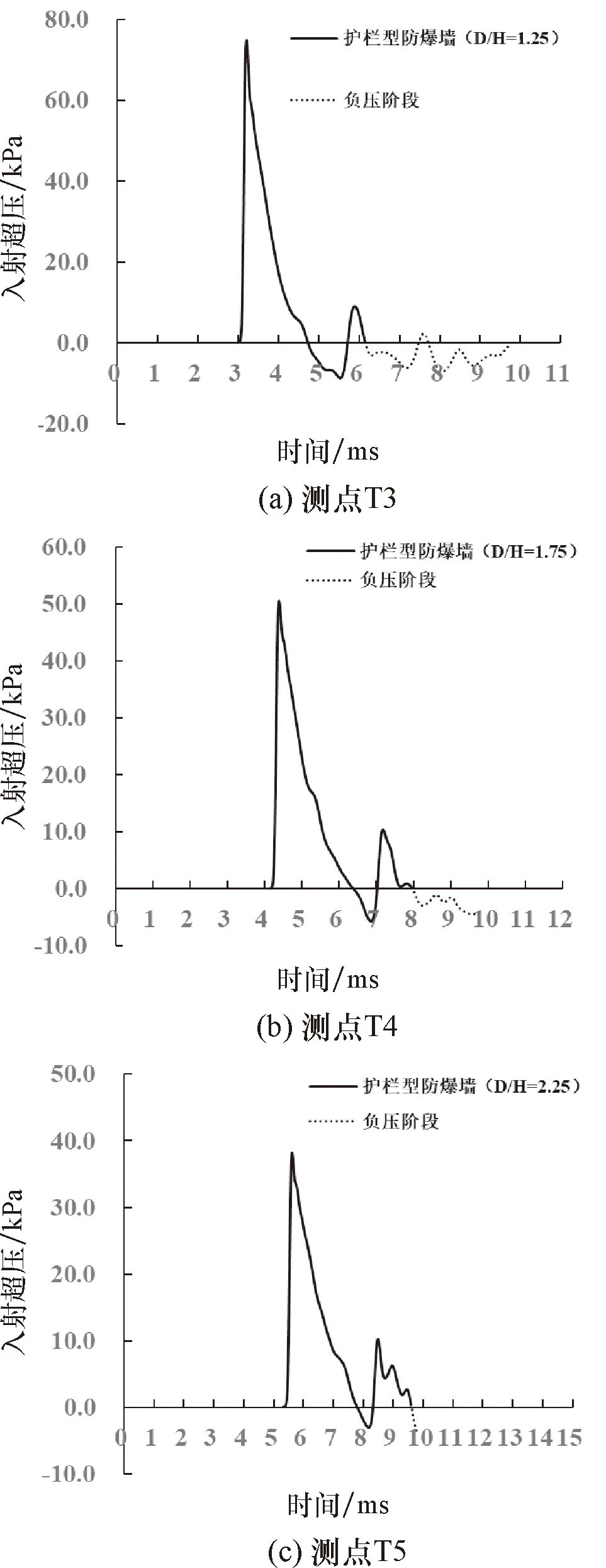
图17 网型防爆墙与护栏型防爆墙在测点T3、T4、T5处的超压时程曲线对比结果

3 结 论

本文通过数值模拟研究，对比了网型防爆墙与护栏型防爆墙在1.0 kg TNT炸药地面起爆、防爆墙与炸药中心距离为1.25 m工况下的墙后爆炸荷载.结果表明，网型防爆墙在超压峰值方面的衰减效果优于护栏型防爆墙，但在冲量方面整体不如护栏型防爆墙，这是由于网型防爆墙后方区域的叠加效应较为显著.因此，在实际应用中，当目标建筑物的墙后距离在0.75倍的墙高范围内时，宜采用网型防爆墙；当目标建筑物与防爆墙的距离超出0.75倍的墙高范围后，应采用护栏型防爆墙.