如何正确运用χ2检验
——高维表资料危险率差分析与SAS实现
2021-09-10胡纯严胡良平
胡纯严,胡良平,2*
(1. 军事科学院研究生院,北京 100850;2. 世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu927@163.com)
在分析来自队列研究设计的g×2×2表资料且选择危险率差作为效应指标时,需要完成以下3 项主要任务:其一,检验各层2×2表资料危险率差是否满足齐性[1-4];其二,估计共同危险率差及其95%置信区间[5];其三,检验共同危险率差是否等于0[5]。本文将介绍前述提及的后两项任务,结合实例并基于SAS 软件完成有关计算,并对SAS 输出结果进行解释,做出统计结论和专业结论。
1 高维表资料共同危险率差分析的基本概念
1.1 高维表g×2×2表资料的表达模式
设高维表g×2×2 表资料的表达模式如下,见表1。
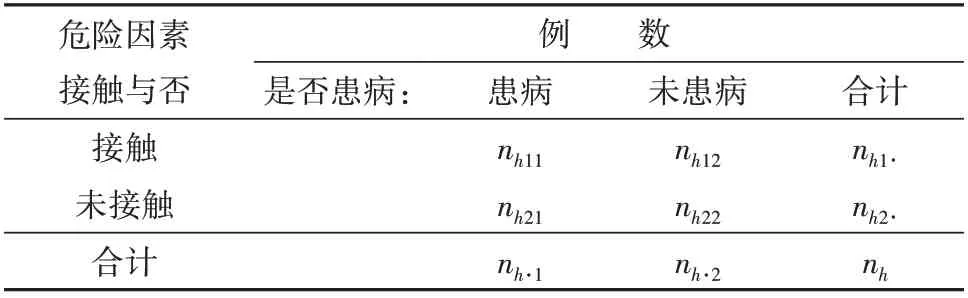
表1 队列研究设计下g×2×2表资料的第h层2×2表资料的表达模式
1.2 高维表资料共同危险率差的含义

【说明】基于“g×2×2 表资料”对共同危险率差进行分析时,通常首先需要检验各层2×2 表资料是否满足齐性,检验“危险率差”是否满足齐性的具体方法参见文献[1-4],此处从略。
1.3 SAS中FREQ过程估计共同危险率差及其置信区间的方法概述
SAS/STAT 中的FREQ 过程[5]可采用6 种方法估计共同危险率差及其置信区间,分别为:①Mantel-Haenszel 估计法(简称MH 法);②最小风险估计法(简称MR 法);③汇总得分估计法;④Klingenberg 估计法;⑤基于MH 法估计权重的分层Newcombe 估计法;⑥基于MR法估计权重的分层Newcombe估计法。其中,上述前三种方法还可以进行假设检验,即检验共同危险率差是否等于0。
2 高维表资料危险率差分析及SAS实现
2.1 高维表资料危险率差分析的具体算法
2.1.1 高维表资料危险率差分析的具体内容
高维表资料危险率差分析的具体内容包括以下4项:其一,检验资料是否满足齐性要求;其二,估计共同危险率差;其三,估计共同危险率差的置信区间;其四,检验共同危险率差是否等于0。其中,第四项任务可以通过第三项任务间接完成。也就是说,当共同危险率差的置信区间不包含0时,就等于接受“H1:共同危险率差RD≠0”这个备择假设。
2.1.2 高维表资料共同危险率差的点估计及置信区间估计
2.1.2.1 Mantel-Haenszel估计法
Mantel 和Haensael 于1959 年提出了分层权重,Sato 于1989 年提出了Sato 方差估计量[5],在此基础上,构建出Mantel-Haenszel估计法[5]。

检验假设:H0:σMH=0,H1:σMH≠0,检验的显著性水平为α。其检验统计量见式(8):

2.1.2.2 最小风险估计法
Mehrotra 和Railkar 于2000 年提出了最小风险估计法[5]。
第1 步,基于最小风险估计法估计高维表资料共同危险率差d^MR(简称MR估计量),见式(9):

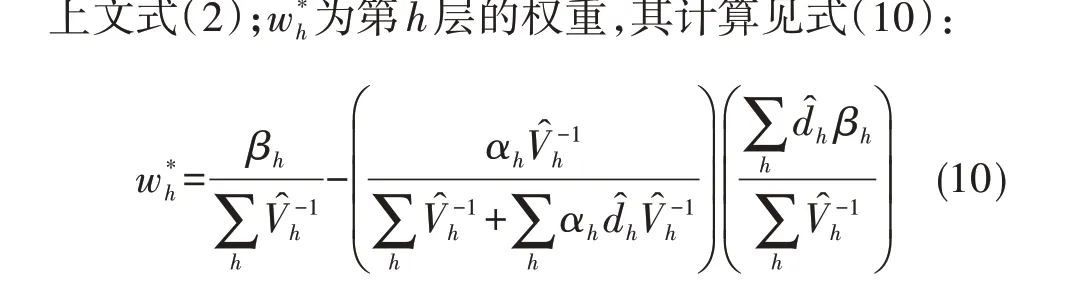
在式(10)中,αh和βh的计算分别见式(11)、式(12):
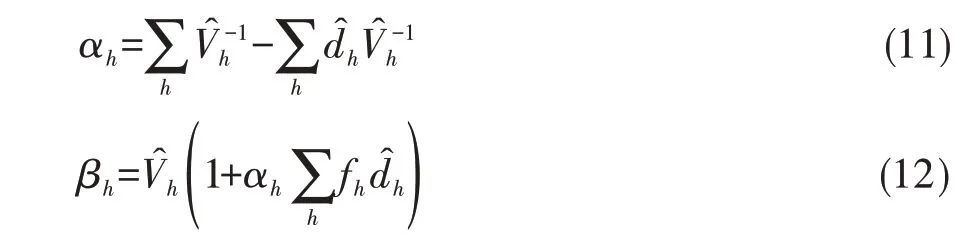
在式(12)中,fh是第h层的分数,其计算见式(13):

在式(16)中,C为连续性校正数,其计算见式(17):


2.1.2.3 汇总评分估计法
Agresti于2013年提出了汇总评分估计法[5]。

第h层风险率差评分的100(1-α)%置信区间见式(25):

第2步,构建风险率差的汇总评分的100(1-α)%置信区间,见式(26):

2.1.2.4 Klingenberg估计法
基于Mantel 和Haensael's 共同风险率差以及Sato 方 差 估 计 量,Klingerberg 于2014 年 提 出 了Klingerberg 估计法[5]。
第1 步,基于Klingerberg 估计法估计高维表资料共同危险率差的置信区间中点,见式(29):
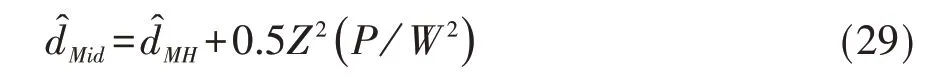
第2步,构建风险率差的Klingerberg's 100(1-α)%置信区间,见式(30):

在式(29)、式(30)、式(31)中,有关变量的定义如下:
P=∑hPh,Q=∑hQh,W=∑hwh;wh、Ph和Qh的计算分别见式(3)、式(6)和式(7)。
2.1.2.5 分层Newcombe估计法
Yan 和Su 于2010 年提出了分层Newcombe 估计法[5]。该法是基于分层的Wilson 置信区间法经过改造后构建而成。设合并后的2×2 表的第1 行上比例的Wilson 置信限的下限与上限分别为L1与U1;其第2 行上比例的Wilson 置信限的下限与上限分别为L2与U2。于是,共同危险率(或比例)差的100(1-α)%分层Newcombe 置信限的下限与上限分别为L与U,其计算见式(32)、式(33):
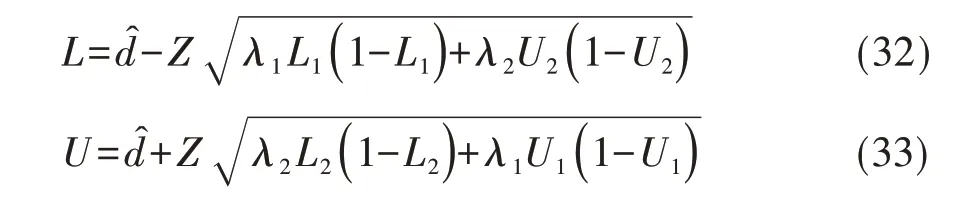
在式(32)、式(33)中,λ1与λ2的计算分别见式(34)、式(35):

2.2 高维表资料共同危险率差分析的SAS实现
2.2.1 问题与数据
【例1】文献[4,6]提供了如下资料,见表2。试对7项研究的共同危险率差进行分析。
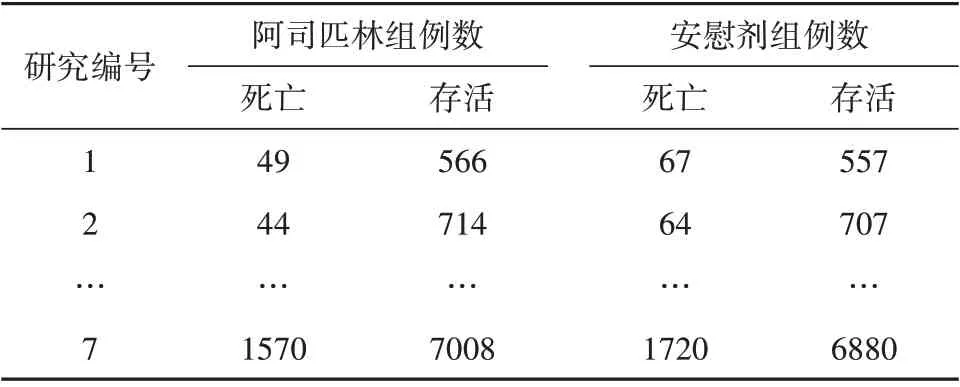
表2 阿司匹林预防心肌梗死后患者死亡与否的7项随机对照研究结果
2.2.2 对例1资料共同危险率差分析的SAS实现
【例2】沿用例1 中的“问题与数据”,试对7 项研究的共同危险率差进行分析。
【分析与解答】设所需要的SAS程序如下:

【程序说明】在“tables 语句”中有3 个选项,在选项“cmh”后指定了进行优比齐性检验的3种方法;在选项“commonriskdiff”后指定了进行共同危险率差检验的3 种方法;在选项“cl”后指定了进行共同危险率差置信区间估计的6种方法。
【SAS输出结果及解释】
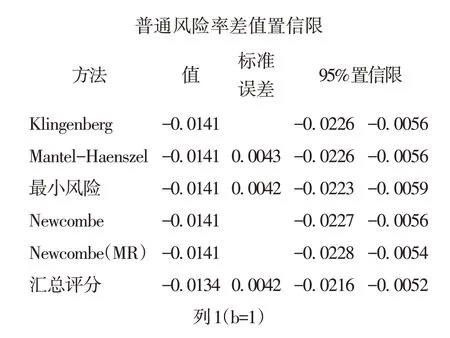
以上输出的是关于共同危险率差的6种置信区间估计结果,第2列为“阿斯匹林与安慰剂治疗后死亡率之差值的估计值”,差值为负值,表明阿司匹林组的死亡率低于安慰剂组的死亡率,6 种方法得到的共同危险率差的95%置信区间都没有包含0,表明“共同死亡率差不等于0”,即阿斯匹林与安慰剂治疗后死亡率之间的差别有统计学意义,在治疗心肌梗死时,阿斯匹林的治疗效果比安慰剂好。

以上输出的是关于共同危险率差是否等于0的3 种检验结果,均得到P<0.01,说明阿斯匹林与安慰剂治疗后死亡率之间差异有统计学意义,在治疗心肌梗死时,阿斯匹林的治疗效果比安慰剂好。

以上是采用Cochran-Mantel-Haenszel 法(简称CMH 法)对合并的2×2 表资料进行3 种假设检验的结果,表明“两种药物(阿斯匹林与安慰剂)”与“两种治疗结果(死亡与生存)”之间存在关联性(因第3 行上的备择假设为“一般关联”),具体地说,即阿斯匹林治疗的死亡率低于安慰剂治疗的死亡率。

以上输出的是“普通优比和相对风险”的计算结果,其中,“普通”也叫做“共同或合并”。实际上,就是基于“Mantel-Haenszel 法”和“logit法”计算出来的校正“共同相对危险度”的估计值及其95%置信区间。在本例中,应看“相对风险(第1 列)”的两种方法计算的结果(因为第1列上的结果为“死亡”,是研究者特别关注的结局)。RRMH=0.9143,其95%置信区间为[0.8664,0.9649];RRL=0.9145,其95%置信区间为[0.8665,0.9651]。两种方法得到的置信区间都不包含1,表明共同相对危险度小于1,即阿斯匹林对应的死亡率小于安慰剂对应的死亡率。
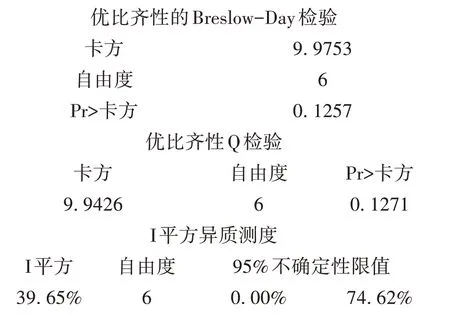
以上是基于“优比的齐性检验”结果,可作为基于“危险率差的齐性检验”结果的参考。结果显示,资料满足齐性要求。
【统计结论与专业结论】在本例中,因95%置信区间不包含1,说明共同相对危险度与1之间的差别具有统计学意义。由于RR=0.9145<1,说明阿司匹林对应的死亡率低于安慰剂对应的死亡率。也就是说,相对于采用安慰剂而言,采用阿司匹林预防心肌梗死可明显降低心肌梗死患者的死亡率。这与前面基于“普通风险率差值置信限”计算结果所得结论是完全相同的。
3 讨论与小结
3.1 讨论
在SAS/STAT 的FREQ 过程[5]中,只给出了针对“优比”的齐性检验,未给出针对“相对危险度”和“危险率差”的齐性检验(一般来说,对同一个资料而言,前述提及的几种齐性检验结果基本接近,故在要求不高的前提下,可以将“优比的齐性检验结果”作为“危险率差的齐性检验结果”的近似解);SAS 基于6 种方法给出了关于共同危险率差及其置信区间的估计公式,其中,有3 种方法还可以直接对“共同危险率差是否等于0”进行假设检验。但SAS 并没有明确交代前述提及的6 种方法哪些仅适用于“资料满足齐性要求”,哪些方法适用于“资料不满足齐性要求”。当使用者需要基于“危险率差”进行“Meta 分析”时,解决的办法有两种:其一,基于相 应 的 公 式 和SAS 语 言 编 程[1,3-5,7-8]实 现 计 算;其二,使用专门用于Meta 分析的RevMan 软件[9-10]实现计算。
3.2 小结
本文对g×2×2 表资料进行了危险率差分析,其内容包括6 种“危险率差的点估计和置信区间估计方法”和3 种关于“危险率差是否等于0”的检验方法。通过一个实例并基于SAS软件实现了危险率差分析,并对SAS输出结果进行了解释,做出了统计结论和专业结论。
