篮球上的一笔画
2021-09-10马济敏
马济敏

有不少同学都喜欢打篮球,可是篮球上也有数学,你知道吗?
从上面的这个篮球上你看到了什么?红色的皮,还有黑色的条纹。对了,就是这个黑 色的条纹!
如果你用手指沿着这些黑色的纹路移动,能不能连续不断又不重复地把所有的线都走完呢? 等你找一个篮球来亲自试一试吧。不过估计你比画一会儿就没了头绪,走乱套了。这是因为篮球上的线条纵横交错,从哪儿开始,到哪儿拐弯,到何处结束都需要斟酌一番。 如果你是一个数学爱好者,那就不用费这些事了!因为我们首先会想道:找规律。把“篮球问题”转化成“数学问题”,把球体转化成简单的平面图形来研究。这就是能否“一笔画”的问题。
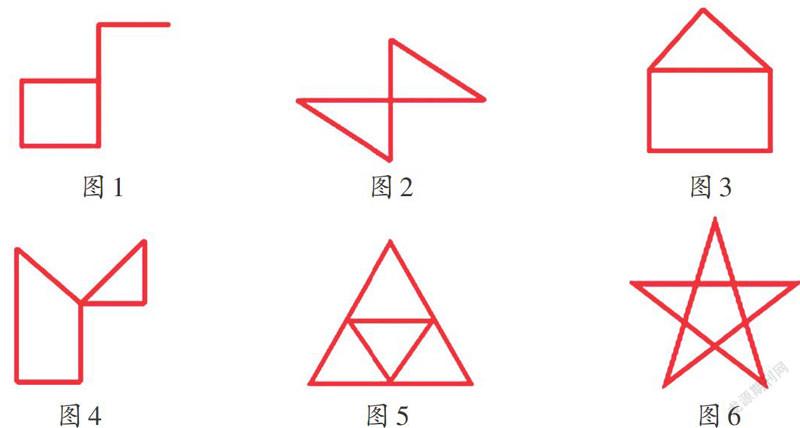
所谓“一笔画”,就是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。 “一笔画”是一种有趣的数学游戏。那么什么样的图形可以一笔画成呢?我们先找几个简单 的图形试一試。
比如:
这 6 个图形都能一笔画成,它们之中藏着什么秘密呢?这个“秘密”就是图形中的“点”。比如图1、4、5 中有6 个端点,图2、3 中有5 个端点,图6 中有10 个端点。在这些端点中,有的从一点出发引出2 根线、4 根线,有的引出1 根线、3 根线。
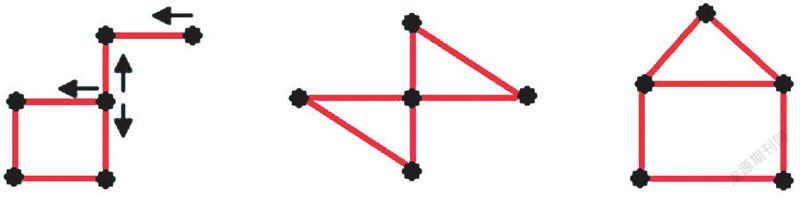
如下图:
我们把引出双数条线的端点叫作偶点,引出单数条线的点叫作奇点。图 1 中有 2 个奇点,4 个偶点;图3 中有2 个奇点,3 个偶点;图2、4、5、6 中全是偶点。
如果是3 个、4 个甚至更多的奇点能否一笔画成呢?画图验证:
这几个图形都不能一笔画成。
由上面的操作我们可以做这样的猜想:如果一个图形是连通的,那么,1.图中有0 个奇点(全是偶点) 的图形可以一笔画成,而且可以以任意一点为起点;
2.图中有2 个奇点的图形也能一笔画成。作一笔画时,它们都是从一个奇点出发,最后回到另一个奇点。
3.像“十”“大”这样的图形,奇点的个数既不是0 个又不是2 个的,无论怎样都不能一笔画成。
有了这样的发现,我们就可以对篮球上的黑条纹进行数数了。黑条纹形成了6 个偶点, 没有奇点,那当然能够一笔画成了!
最后还要告诉你一个“小秘密”:关于“一笔画”的问题,早在18 世纪,著名的数学家欧拉就已经通过研究“七桥问题”,得到并证明了更为广泛的有关一笔画的三条结论,人们通常称之为“欧拉定理”。不过他可能没有想到的是,今天我们竟然用篮球来研究“一笔画”?
聪明的同学,再在篮球上试一试,是不是就很简单了?
