典型声爆研究模型近场预测统计量化分析评估

瞿丽霞 徐悦 韩硕 王宇航

摘要：声爆预测是超声速民机设计的关键技术。排除认知不确定性因素外，近场声爆预测能力的成熟度主要取决于所采用的计算流体力学（CFD）求解方法捕捉激波间断的能力。以共用研究模型旋成体和三角翼作为研究对象，选取典型截面声爆信号过压峰值强度和位置为系统响应量，开展了初步的不确定度量化分析评估。结果表明，当前对简单构型的预测还不够准确，声爆信号近场预测能力的成熟度还有待进一步提高。需要进一步发展高可信度声爆预测方法，准确捕捉飞机近场空间脱体压力；针对所关注的系统响应量，开展更加具体的不确定度量化评估分析研究。

关键词：超声速民机；声爆；预测；统计分析；不确定度量化

中图分类号：V211.3文献标识码：ADOI：10.19452/j.issn1007-5453.2021.04.003

准确预测声爆是超声速民机研制过程中进行声爆水平评估和抑制的前提，是绿色超声速民机发展中的重要研究课题[1-2]。声爆是一种典型的多尺度现象，其近场激波诱导压力扰动的特征尺度约为飞机的特征尺度，该近场压力扰动会在大气中传播到约为飞机特征尺度几百倍的远场。在超声速民机的详细设计阶段和适航评估阶段，均需要高精度的声爆预测方法对其产生的声爆强度进行评估。目前国内外发展的声爆预测方法主要有线化理论方法、全域计算流体力学（CFD）预测方法和混合预测方法。混合预测方法凭借计算量适中、精度较高，能够充分考虑飞机外形、飞行状态和声爆真实大气传播特性的优势，成为当下最主要的声爆预测方法，广泛应用于声爆传播演化过程研究、超声速民机低声爆布局设计与优化、超声速飞行地面声爆社区响应和演示飞行验证等领域[3-5]。

自20世纪50年代开始，国际上针对声爆预测开展了系统性研究[6]。近年来，美国航空航天学会（AIAA）针对声爆预测方法在世界范围内组织了持续的可信度研究活动，在2014年[7]、2017年和2020年分别召开了三届声爆预测研讨会，研讨会提供了若干声爆共用研究模型供参与者进行验证确认研究，对声爆近场预测及远场传播预测方法和工具进行分析评估。在国内，中国航空研究院（CAE）于2019年开始组织相关科研机构开展了系统的高可信度声爆预测工具的验证确认计算研究（Cgroup）。第一期参加单位包括航空工业气动院（ARI）、西北工业大学（NPU）、航空工业计算所（ACTRI）和航天十一院（CAAA）等。

本文概述了超声速民机近场声爆预测方法，重点对典型声爆研究模型的近场预测结果开展了不确定量化分析，对未来超声速民机近场声爆预测研究的发展方向提出了几点建议。

1近场声爆预测方法

CFD方法已非常成熟，能够准确捕捉飞行器表面流动特征，获得可靠的气动力数据。但近场声爆预测需要捕捉近场空间发展的脱体压力信号，而声爆信号量级相对较小，很难准确模拟。近场声爆预测精确与否关键在于近场空间波系的精确捕捉。国内外学者对近场声爆预测方法的研究主要集中在网格量、网格拓扑结构、空间离散格式和湍流模型等因素对近场波形的影响方面[8-12]。对于网格拓扑的共识是，通常需将计算域设计为马赫锥构型，锥体马赫角β由来流马赫数Ma确定（sinβ=1/Ma）。对于一些简单标准模型，求解欧拉方程的近场声爆预测精度是令人满意的。对于外形比较复杂的超声速全机构型，由于各部件之间的干扰激波系非常复杂，边界层会显著影响激波的强度和位置分布，这种情况下，求解RANS方程的声爆预测方法逐渐得到全球研究者的共识，而不同湍流模型对边界层的处理方式也会间接影响其对近场空间波系的捕捉能力。另外，自适应网格方法和高精度格式等被引入声爆预测中，以提高近场过压分布的预测精度和效率。

2不确定度量化理论

3近场声爆信号预测结果不确定度量化分析

3.1旋成体模型

旋成体模型是SBPW1选用的非升力旋成体模型，可用于对声爆预测技术和试验预测能力进行标定。几何构型参考长度L=44.8cm，圆柱段的直径3.54cm，来流马赫数Ma= 1.6。SBPW1会议搜集了21个参加者提供的共计64组数据（两个位置），选用的网格类型包括26组四面体网格、16组混合网格、10组结构网格、4组嵌套网格、3组直角网格、1组 hybrid网格、1组线性网格（linear）；选用的计算模型包括58组Euler、1组层流、3组SA、1组SST和1组线性。Cgroup搜集整理了5家单位提供的36组数据，包括9组四面体网格、19组混合网格、7组结构网格、1组嵌套网格；选用的计算模型包括20组Euler、8组SA和8组SST。

图1（a）给出了沿旋成体模型轴线垂直距离H/L=1.2、周向角Φ=0°处提取近场过压信号。图1（b）～图1（d）给出了不同单位、不同计算网格、不同黏性模型的计算结果与试验数据的对比。总体来说，Cgroup、SBPW1的计算结果与试验数据在头尾激波、压力膨胀段、过压平台等位置的吻合程度较好，头部激波和压力膨胀段与试验曲线均非常贴合，对尾部激波强度的预测相比试验数据略微偏大。最大偏离出现在膨胀区末端的近似小平台区，计算结果和试验曲线的相对误差约为10%。头部激波后的过压平台区，理论上其过压信号为常值，但是试验数据和计算结果均显示出了小振幅的壓力扰动（见图1（c）），这是因为试验模型并非完全轴对称且存在加工瑕疵，大部分计算结果均比较准确地捕捉到了这个压力扰动现象。对黏性影响的研究中发现，相比于RANS方程，Euler方程预测得到的激波位置和强度更接近试验值；在过压平台区，无黏模型的波动曲线更贴近试验数据，而在近似小平台区，黏性模型的计算结果稍好一些。相比于试验值，考虑黏性影响未能提高近场声爆的计算精度，甚至在某些位置Euler方程预测得到的过压信号更为准确。

针对旋成体模型H/L=1.2、周向角Φ=0°位置的头尾激波过压峰值和位置，将SBPW1和Cgroup的所有数据进行了统计分析对比，如图2、图3所示。与试验数据相比，头激波过压峰值大部分都落在了试验误差带上限范围内，尾激波过压峰值和头尾激波过压峰值对应的位置（X值，单位m）则分散度较大。头尾激波过压峰值位置的试验值误差相当小，误差量级基本在10-4m，而国内外预测值分散度误差量级均为10-3m左右。SBPW1预测得到的头激波过压峰值的中值偏离试验均值约3.5%、位置中值偏离约0.5%，Cgroup的头激波过压峰值的中值偏离试验均值约5.0%、位置中值偏离约0.6%。尾激波过压峰值预测值的绝对值均偏大，SBPW1的尾激波过压峰值的中值偏离试验均值约22%、位置中值偏离约0.27%，Cgroup的尾激波过压峰值中值偏离试验均值约16%、位置中值偏离约0.17%。SBPW1预测得到的头激波强度和位置的分散度分别为0.00083m和0.0040m，Cgroup预测得到的头激波强度和位置的分散度分别为0.00079m和0.0025m；SBPW1预测得到的尾激波强度和位置的分散度分别为0.00241m和0.0059m，Cgroup预测得到的尾激波强度和位置的分散度分别为0.00216m和0.0096m。

可见，国内外对头激波过压峰值及位置的预测中值与试验均值的误差均在5%以内，但SBPW1预测结果的分散度相对较大。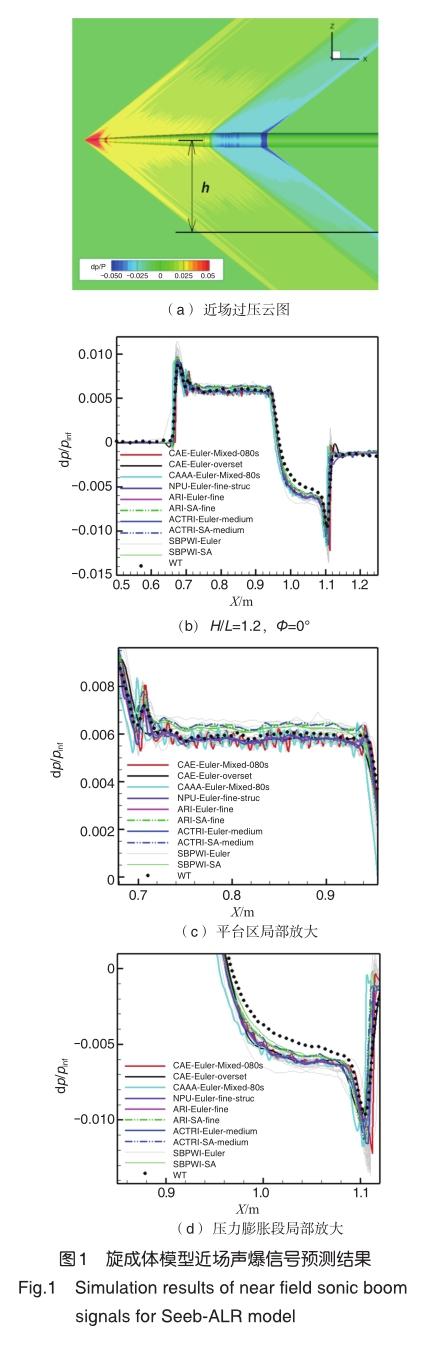

图4和图5对比了不同网格类型、密度对旋成体模型头尾激波过压峰值和位置的预测结果。其中，选用了SBPW1提供的三组共用网格数据结果，包括混合网格（Mixed）、四面体网格（Tet）、USM3D，网格密度分别为0.8、1.0、1.25、1.56、2.0；Cgroup提供了Mixed网格的结果。总体来看，网格密度越大，头尾激波过压峰值的预测结果分散度越小；混合网格对头激波过压峰值的预测相对较好。Cgroup对尾激波过压峰值位置的预测偏差较大。

可见，国内外对旋成体模型尾激波强度的预测值大部分都比试验值大，且分散度比头激波均高出一个量级，尾激波过压峰值位置的分散度也较大。头尾激波峰值位置的试验值误差很小，而预测结果分散度相对较大。后续还需要进一步开展研究以提高旋成体模型尾激波，以及头尾激波峰值位置的预测水平，定量分析网格、湍流模型等因素对计算结果不确定度的影响。

3.2三角翼模型

三角翼模型是SBPW1采用的无弯度、对称的翼身融合体模型，属于简化的升力体构型，参考长度L=6.898in，来流马赫数Ma=1.7。会议网站上搜集了20个参加者提供的共计60组数据（10个位置），选用的网格类型包括24组四面体网格、19组混合网格、8组结构网格、4组嵌套网格、2组直角网格、1组hybrid网格；选用的计算模型包括56组Euler、4组SA。Cgroup的计算结果包括5家单位的34组数据，选用的网格类型包括26组混合网格、2组结构网格；选用的计算模型包括21组Euler、7组SA、6组SST。

图6（a）以三角翼模型轴线为旋转中心，在不同旋转半径处截取的过压计算结果云图，可以明显看出不同方位角Φ的过压分布变化。图6还给出了三角翼模型在H/L=3.6，不同周向角（Φ=0°、30°、60°、90°）的过压计算结果和试验数据的对比。计算结果表明，包括尾支杆在内的各方位角的过压计算结果和试验对比吻合较好，头部激波的强度与试验值偏差相对较小。相对于头部激波，机翼前缘激波和尾部激波的峰值预测值偏大，这可能是试验模型加工时，对机翼的各个边缘处做了光滑处理而降低了激波强度，而大部分参与者未对计算模型进行相应修形。随着方位角的变化，尾部激波从单个激波演变为多激波的演变过程均与试验曲线表现的变化规律基本一致。

图7和图8以三角翼模型近场H/L=3.6、周向角Φ=0°位置的声爆信号头尾激波峰值及峰值位置的预测结果为例进行不确定度量化分析。总体来说，Cgroup的预测结果分散度相对较低。头激波和第一个膨胀波过压峰值的预测值基本都在试验误差带范围内，但对激波峰值的位置预测均不太理想。激波过压峰值位置的试验值误差相当小，误差量级基本在10-6m，而国内外预测值分散度误差量级均为10-3m左右。SBPW1的机翼前缘激波过压峰值的中值与试验值相比偏差达到了20.9%，Cgroup相应的偏差为18.0%；SBPW1的尾激波过压峰值的中值与试验值相比偏差达到了15.1%，Cgroup相应的偏差为4.6%。其中，SBPW1预测得到的头激波过压峰值的分布区间可表示为0.01090±0.00280，头激波位置的分布区间为0.86204±0.00968；Cgroup预测得到的头激波过压值的分布区间可表示为0.01029±0.00146，头激波位置的分布区间为0.86325±0.003515。可见，相比SBPW1的结果而言，Cgroup的頭激波预测结果分散度较低；三角翼模型机翼前缘之后的声爆信号以及头尾激波峰值位置的准确预测还需要进一步研究，并定量分析网格、湍流模型等因素对计算结果不确定度的影响。

4结论

对近场声爆信号的预测本质上是采用CFD方法模拟空间过压信号的过程，这与传统飞机气动力计算中重点关注机体表面气动力参数是完全不同的。因此，排除认知不确定性因素，近场声爆预测能力成熟度主要取决于所采用的CFD求解方法捕捉激波间断的能力。采用SBPW1提供的旋成体和三角翼兩个共用研究模型，选取典型截面声爆信号过压峰值强度和位置作为系统响应量，开展初步的不确定度量化分析评估，并给出了分布区间。从近场声爆预测结果可以得出，国内外预测均呈现最大过压的预测接近试验值，波形峰值位置误差较大的特征。其中，旋成体模型和三角翼模型的声爆信号头激波过压峰值的强度预测值基本都分布在试验误差带上限或偏大，且尾激波过压峰值强度预测值偏差更大；头尾激波过压峰值位置预测值的分散度比试验结果则要大1～3个量级。建议未来可在如下两方面开展研究：

（1）发展可准确描述复杂全机构型近场声爆信号的高可信度预测方法，包括更先进的高阶离散格式和网格自适应方法、带发动机喷流的复杂后体流场模拟方法等，从而尽可能地精确捕捉飞机近场空间脱体压力。

（2）国内对超声速民机的声爆预测研究处于相对分散状态，研究成果难以快速积累和继承，因此应集中力量突破声爆预测中的关键难点，组织开展较大规模的声爆预测可信度研究，以提升国内声爆预测工具的技术成熟度和工程可用性，具体包括声爆预测验证确认计算研究、超声速民机声爆标模设计与风洞试验等。

参考文献

[1]兰世隆.超声速民机声爆理论、预测和最小化方法概述[J].空气动力学学报，2019，37（4）：646-654. Lan Shilong. Overview of sonic boom theory， prediction and minimization methods for supersonic civil aircraft[J]. Acta Aerodynamica Sinica， 2019， 37（4）： 646-654.（in Chinese）

[2]徐悦，韩忠华，尤延铖，等.新一代绿色超声速民机的发展现状与挑战[J].科学通报， 2020，26（2-3）：127-133. Xu Yue， Han Zhonghua， You Yancheng， et al. Progress and challenges of next generation green supersonic civil aircraft[J]. Science China， 2020， 26（2-3）：127-133.（in Chinese）

[3]韩忠华，乔建领，丁玉临，等.新一代环保型超声速客机气动相关关键技术与研究进展[J].空气动力学报，2019，37（4）：620-635. Han Zhonghua， Qiao Jianling， Ding Yulin， et al. Key technologiesfornext-generationenvironmentally-friendly supersonic transport aircraft： a review of recent progress[J]. ActaAerodynamica Sinica， 2019， 37（4）： 620-635. （in Chinese）

[4]韩阳，冷岩，杨龙，等.一类超声速长航程民用客机的气动设计和性能评估[J].航空科学技术，2019，30（9）：25-32. Han Yang， Leng Yan， Yang Long， et al. Aerodynamic design and evaluation of a type of supersonic long-range civil transport[J]. Aeronautical Science & Technology，2019，30（9）： 25-32. （in Chinese）

[5]钱战森，韩忠华.声爆研究的现状与挑战[J].空气动力学报， 2019，37（4）：601-619. Qian Zhansen， Han Zhonghua. Progress and challenges of sonic boom research[J]. Acta Aerodynamica Sinica， 2019， 37（4）： 601-619. （in Chinese）

[6]Domenic J M，Percy J B，Kenneth J P，et al. Sonic boom：six decades of research[R]. NASA/SP-2014-622，2014.

[7]Michael A P，John M M. Summary and statistical analysis of the first AIAA sonic boom prediction workshop[R]. AIAA 2014- 2006，2014.

[8]徐悦，宋万强.典型低声爆构型的近场声爆计算研究[J].航空科学技术，2016，27（7）：12-16. Xu Yue，Song Wanqiang. Near field sonic boom calculation on typicalLSBconfigurations[J].AeronauticalScience& Technology， 2016，27（7）：12-16. （in Chinese）

[9]王刚，马博平，雷知锦，等.典型标模声爆的数值预测与分析[J].航空学报，2018，39（1）： 169-181. Wang Gang， Ma Boping， Lei Zhijin， et al. Simulation and analysis for sonic boom on several benchmark cases[J]. Acta Aeronautica et Astronautica Sinica， 2018， 39（1）： 169-181. （in Chinese）

[10]李典，蒋城，陈智，等.非结构网格伴随各向异性自适应声爆近场计算[J].航空计算技术，2018，48（5）：34-37. Li Dian， Jiang Cheng， Chen Zhi， et al. Adjoint-based anisotropic unstructured grid adaptation for sonic boom near field computation[J]. Aeronautical Computing Science， 2018， 48（5）： 34-37. （in Chinese）

[11]马博平，王刚，雷知锦，等.网格对声爆近场预测影响的数值研究[J].西北工业大学学报，2018，36（5）： 865-874. Ma Boping， Wang Gang， Lei Zhijin， et al. Numerical investigation of influence of mesh property in nearfield sonic boom prediction[J]. Journal of Northwestern Polytechnical University， 2018， 36（5）： 865-874. （in Chinese）

[12]冷岩，钱战森，刘中臣.超声速条件下旋成体声爆典型影响因素分析[J].空气动力学学报，2019， 37（4）：655-662. Leng Yan， Qian Zhansen， Liu Zhongchen. Analysis on typical parameters of bodies of revolution affecting the sonic boom[J]. ActaAerodynamica Sinica， 2019， 37（4）：655-662. （in Chinese）

[13]Morrison J H. Statistical analysis of CFD solutions from the fourthAIAAdrag prediction workshop[R].AIAAPaper，2010.

[14]Rumsey C L，Long M，Stuever R A，et al. Summary of the firstAIAACFD high lift prediction workshop[R].AIAAPaper， 2014.

（责任编辑余培红）

作者简介

瞿丽霞（1986-）女，博士，高级工程师。主要研究方向：计算流体力学、空气动力学、航空数值模拟技术。

Tel：010-84933672

E-mail：qulixia@cae.ac.cn

徐悦（1979-）男，博士，研究员。主要研究方向：空气动力学、流动控制。

Tel：010-84929359

E-mail：xuyue@cae.ac.cn

韓硕（1993-）男，硕士，工程师。主要研究方向：空气动力学。

Tel：010-84922696

E-mail：hanshuo@cae.ac.cn

王宇航（1991-）男，硕士，工程师。主要研究方向：飞行器设计、空气动力学。

Tel：15810113662

E-mail：yunmengjingtian@163.com

Quantitative Statistical Analysis of Near Field Sonic Boom Prediction on Typical Research Models

Qu Lixia*，Xu Yue，Han Shuo，Wang Yuhang

Chinese Aeronautical Establishment，Beijing 100012，China

Abstract： Sonic boom prediction is addressed as a key issue in supersonic civil aircraft design. Excluding epistemic uncertainty， the maturity of near-filed sonic boom predictive capability mainly depends on the capability of computational fluid dynamics （CFD） methods adapted to capture shock wave discontinuities. A statistical analysis is presented for an axisymmetric body （seeb-ALR） and simple delta wing body （DWB）， focusing on the shock strength and locations， which are set in terms of system response quantities （SRQs） for preliminary uncertainty quantification estimation. Overall， the maturity of near-filed sonic boom predictive capability needs to be further improved， as it is not accurate enough for a simple configuration. It is necessary to develop highly credible prediction methods that can accurately describe near-field sonic boom signatures so as to capturing off-body pressure. Research focus should not only be on overpressure strength of nose shock， tail shock， wing leading edge shock， but also on the shock positions. More specific uncertainty quantification analysis needs to be further conducted for SRQs of interest.

Key Words： supersonic civil aircraft； sonic boom； prediction； statistical analysis； uncertainty quantification