基于模糊与一致性复合智能算法的“源-网-荷-储”协同控制策略研究

张林垚，黄东明，王彦铭，陈垣玮，倪识远

（1.国网福建省电力有限公司经济技术研究院，福建 福州 350012；2.国网泉州供电公司，福建 泉州 362000；3.国网福州供电公司，福建 福州 350004）

随着社会生产生活水平的不断提高，传统化石能源仍占据着能源消耗的主要地位，不仅造成了环境恶化和全球温室效应，还导致以石油、煤炭为主的传统能源耗竭，进而引发能源短缺问题[1-2]。因此，清洁能源成为了能源发展的必然趋势，亟待通过清洁能源的发展改革现有能源结构[3-4]。随着国家层面上通过出台一系列相关政策促进新能源发展，进一步引领电力电子技术等新兴技术与产业发展，特高压、储能、抽水蓄能、综合能源、增量配电等迎来发展关键窗口，电力系统供电模式将从单一能源供应侧转化为双边“源荷互动”复杂多边系统，满足可再生能源大规模并网、输送以及消纳，同时也给电网安全、可靠的运行造成了挑战[5-6]。

由于可再生能源存在不确定性、间歇性特征，并网后将影响用电侧连续、可靠用电。因此，充分发挥多种电源、电网平台、负荷之间的特点，借助电网和负荷控制的灵活性、电源之间互补性、储能可调性，达到“源-网-荷-储”动态调节和相互协调，提升负荷和电源之间稳定供应抵抗风险能力[7]。然而目前主要是针对其中的2～3个因素的协同作用进行了研究，例如：源-源[8]、源-网[9]、网-荷-储[10]以及源-网-荷[11]等，然而目前综合分析“源-网-荷-储”4个因素的协同控制方法仍鲜有研究。

针对主动配电网的协同优化方法通常采用集中优化法、分布优化法以及智能算法[12]。集中式优化算法通过集中中心与主动配电网内所有源、网、荷、储建立联系实现信息交换，如拉格朗日乘子法[13-14]。分布式算法则是通过减小模型的复杂度，提高求解效率，如拉格朗日松弛法、交替乘子迭代法等[15-16]。智能算法能够在多目标、非线性的环境中寻找最优解，具有较好的全局优化能力和鲁棒性，常用的有粒子群算法、遗传算法等[17]。然而，在如今的配电网系统中可再生能源渗透率高，其传统的优化方法已经无法满足实际需求。因此，亟待研究一种能够综合考虑“源-网-荷-储”协同控制策略，其对电网系统发展是至关重要的。

本文为了优化“源-网-荷-储”协同控制策略，针对基于模糊与一致性复合智能算法的“源-网-荷-储”协同控制策略展开了一系列研究。首先分析“源、网、荷、储”4个因素的基础特性和互动特性，其次结合电源、储能、负荷的反馈特征和风电的不稳定性，从而构建系统的动态协调最佳控制模型，提出通过用模糊策略改进粒子群算法再结合一致性算法的复合智能算法，然后针对相关算例进行求解，进而验证该策略的可靠性，其结果具有一定的工程实际意义。

1 源网荷储互动特性

1.1 源-网-荷-储基础特性

“源-网-荷-储”的全面互动以及协同调节是主动配电网协同控制的必然趋势，通过多种技术与管理手段，促进电力系统动态平衡能力提升及实现资源最大化经济化调度模式[8-12]。

1.1.1 源层特性

电源层是主动配电网的源头，主要有可调度同步机组、新型双馈感应风机、传统异步感应风机和交直流互相转换的光伏发电系统。可调度同步机组包括小水电机组和燃气轮机等，具有同步励磁的电压支撑和快速的有功功率调节性能，其在有功功率中对频率变化呈现出负响应特征，在系统频率响应中，其一次调节方式如下：

式中：P，P*分别为同步电机组的实际输出功率及其恒输出功率中的有功功率；α为同步燃气轮机的频率特性系数；Δf为系统实际频率与额定频率的偏差值。

1.1.2 网层特性

随着大量的分布式能源、具有不稳定性的风能和光能并网，使得系统的稳态潮流分布以及电能传输的单一性出现变化，进而影响了系统的安全、稳定和可靠的运行。交互成本CJ与交互功率PJ（t）关系为

式中：Cb（t），Cs（t）分别为t时段内微电网和大电网之间交互功率的购电状态以及售电状态；m（t），n（t）分别为t时段内微电网和大电网之间交互功率的购电价格以及售电价格；N为调度时段总数。

1.1.3 荷层特性

主动配电网中的负荷层对系统的电压以及频率呈现出负反馈特征，即在电力系统的频率增大或者降低时将会引起负荷消耗电功率同步升高或降低，从而对系统频率进行调节，阻碍其频率再增大或减小；若其系统电压增大或减小，将会引起负荷消耗电功率升高或降低，造成电压降的升高或降低，进而阻碍电压再升高或减小。因此，在系统运行优化策略上更应注重实际。电力负荷有功功率的上述特性的静态模型表示如下：

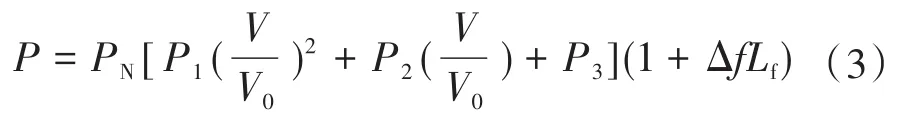
式中：P1，P2，P3分别为系统负荷的恒定阻抗、恒定电流以及恒定功率中的有功功率部分；PN为系统负荷的额定功率；V，V0分别为系统的实时电压以及初始电压；Lf为频率出现变化时对系统负荷所引起的有功功率变化。

1.1.4 储层特性

储能在电源侧可以减小可再生能源的不确定性所带来的影响，有利于可再生新能源的消纳，减小运行成本；在负荷侧则可以完成负荷的削峰填谷，降低备用机组的容量以及提升供电灵活性。模型表示为

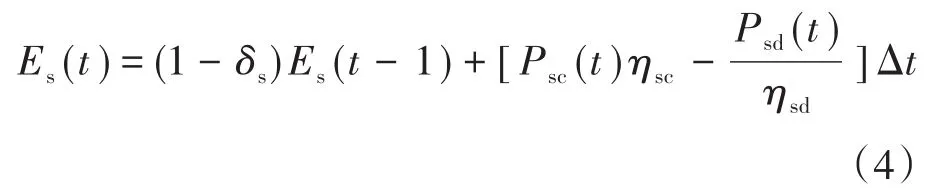
式中：Es（t），Es（t-1）分别为t时段和t-1时段的电储能容量；δs为储能自放电率；ηsc为储能充电效率；ηsd为储能放电效率；Psc（t），Psd（t）分别为充电、放电功率。

1.2 源-网-荷-储协调优化

随着能源互联网的不断深化，“源-网-荷-储”协同控制被赋予更深的意义。在此背景下，“源-网-荷-储”协同调节模式的主要结构如图1所示。“源”指能源资源，主要包括石油、电力、天然气等；“网”指资源网络，主要包括电网、石油管网、供热网等；“荷”不仅表示电力的负荷，还表达用户的能源要求；而“储”则是表示能源资源的多种仓储设施和储备方案。通过能源互联网最终将实现横向多源互补以及纵向“源-网-荷-储”协调[18]。

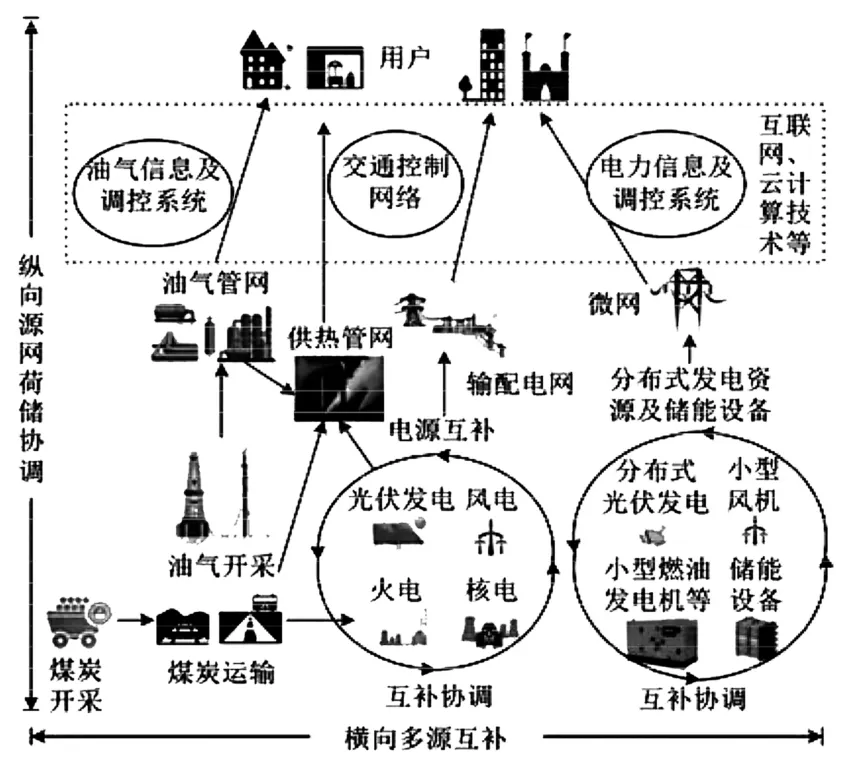
图1 “源-网-荷-储”协同调节模式Fig.1“Source-grid-load-storage”coordinated operation mode

2 源-网-荷-储最佳协同优化模型

将向电网系统输入功率设成正，从系统吸收功率则设成负，则系统中有功功率平衡约束如下：

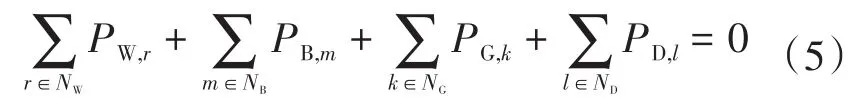
式中：PW，r为再生能源r的有功功率；NW为可再生能源侧的索引；PB，m为储能m的有功功率；NB为储能侧的索引；PG，k为传统发电机k的有功功率；NG为发电机侧的索引；PD，l为负荷l的有功功率；ND为负荷侧的索引。

如果可再生能源输送功率无法全部供给负荷，那么传统发电机的成本关系定义为

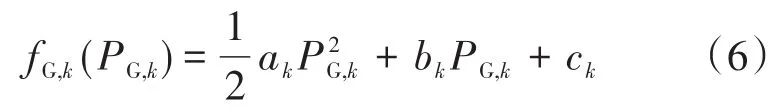
式中：ak，bk，ck分别为机组k的燃料费用系数。机组出力范围如下：

式中：PminG，k为传统发电机k的有功出力下限；PmaxG，k为传统发电机k的有功出力上限。

一般情况下，发电机效率与用户所消耗电量正相关，因此，假设负荷的负利润函数为

式中：al，bl均为负荷利润系数。

弹性负荷具有一定的调节范围：

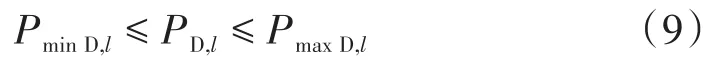
式中：PminD，l为负荷 l的有功出力下限；PmaxD，l为负荷l的有功出力上限。

将损耗近似成负荷的线性函数，从而表达损耗对总成本所产生的影响，损耗为

式中：sl为传输损耗因子。

因此，负荷l实际消耗的功率则为

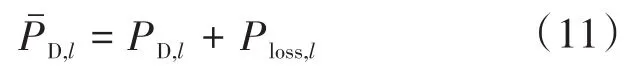
根据电网有功功率平衡约束条件，其损耗也应被考虑：

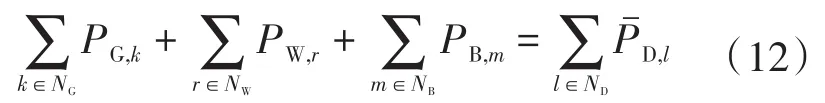
针对储能设备的成本关系表达以及功率约束能够定义为

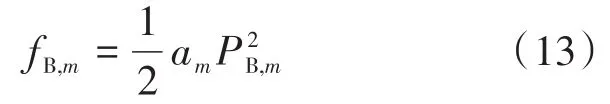
式中：am为储能成本系数。

储能设备具有一定的调节范围：

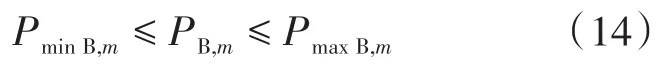
式中：PminB，m表示储能m的有功出力下限；PmaxB，m为储能m的有功出力上限。

系统中决策主体电源、负荷以及储能的成本函数或者其负利润关系如图2所示。

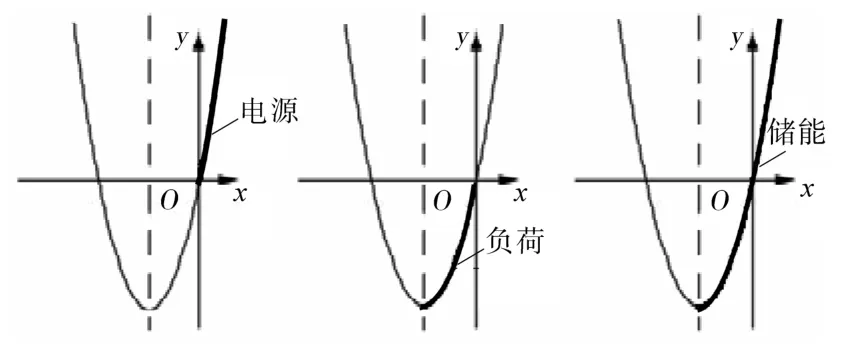
图2 电源、负荷以及储能的成本函数和负利润函数Fig.2 Cost function and negative profit function of power supply，load and energy storage

图2中，参数x和y分别代表了各决策主体的输出功率和成本。电源是电能的生产者，其生产成本和边际成本呈现正相关关系；针对负荷来说，假定其功率是负数，该负利润则随着负荷变大而增大，最终将趋于饱和；针对储能来说，其具有双向性，不仅可以作为源，也是一个负荷，既具有充电功能，也能进行放电。

假设系统中发电机k、负荷l、可再生能源r以及储能m各个决策部分均拥有各自独立的本地代理。为了能够统一且有效地进行分析，将代理i管理功率均用Pi进行表示，该边际成本λi则被定义为

其中，参数i根据需求可取k，l，r以及m。

根据等耗量微增量的规律，各参数的可出力功率被定义为

式中：λ*为边际成本最佳结果。

3 模糊与一致性复合算法控制策略

3.1 模糊化量子行为粒子群算法

在量子行为粒子群算法里，其粒子情况则利用薛定谔方程中的波函数φ（x，t）进行变现，各个粒子均能用各自的吸引子 pi=[pi1，pi2，…，pin]来收敛到一定区域，吸引子可由下式计算得到：

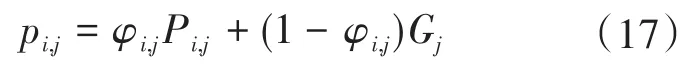
式中：pi，j，Pi，j分别为第 i个粒子所对应的吸引子的第j维以及第i个粒子个体最好位置的第j维；φi，j为一个在[0，1]的范围内，且服从均匀分布的随机数；Gj为全部粒子在整体中最佳位置的第j维。

粒子不断变化位置，其更新公式为

式中：Xi，j为第i个粒子的第j维；u，k均为在[0，1]范围内且服从均匀分布的随机数；α为收缩扩张因子，该值一般能够通过固定取值方法或者线性下降取值方法进行确定；Cj为全部粒子里个体平均最佳位置。

Cj的计算公式为

式中：M为粒子的个数。

针对较为复杂的系统网络，在对同一个位置进行解空间时，可能造成出现并列的两类或者多类的优化对象，则一些特别的情况下，需要对全局最优值展开同步搜索。比如，针对主动配电网的优化控制中，由于其网络节点数量多，并可能还包含有功设备以及无功设备，因此在通过粒子群算法进行协同作用时，将造成该算法过程更加繁琐、迭代速度缓慢、迭代次数多以及编写复杂等问题，此时无法符合全局优化的基本条件。

结合模糊算法对其进行改进，把相同系统中相同位置需要同步展开协调优化的不同类别的控制对象用向量的方式整合成一个粒子。针对n维K个类别的分类，其模糊分类规则的形式如下：

式中：x1，x2，…，xn为 n维模式的向量；Aq1，Aq2，…，Aqn为模糊集对应的语言变量；cs，w分别分数据项的支持度和信任度；CFq为规则的置信度；Cq为决策的分类编码，取值为1，2，…，K。

针对各种基础数据展开模糊化处理后，将其输入模糊分类系统，且隶属关系如图3所示。

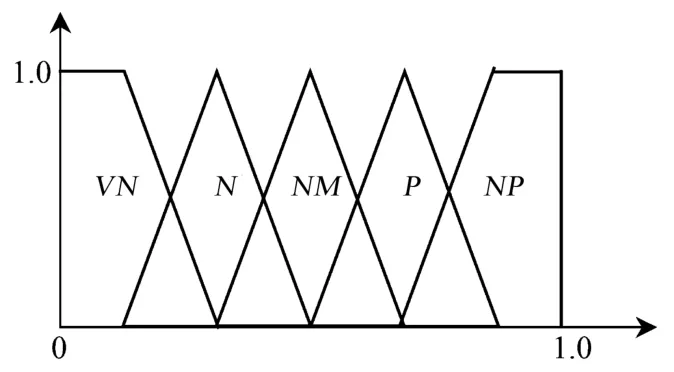
图3 隶属函数Fig.3 Membership degree

图3中，模糊子集的隶属度等级共分为5级，从左至右依次为极低、低、正常、高、极高。

令一个m维空间中，相同位置的多个不同类别的粒子同步进行更新，则其改进型的粒子定义为

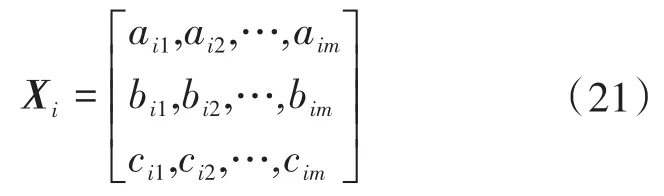
式中：aim，bim，cim分别为解空间内同一位置不同类别的粒子。

若第i个粒子处于目前搜索到的最佳位置，则叫作个体极值；若全部粒子均处于搜索到的最佳位置，则叫作分类位置。根据分类的结果，利用一致性算法进一步改进协同优化策略。

3.2 一致性算法的协同优化策略

一致性算法表示各个代理自行获取本地数据，且与相邻的代理进行边界信息互通，从而进行分布解析。依据一致性算法，每个代理只使用本地及相连空间代理共享信息，代理i的信息更新过程能够被定义为

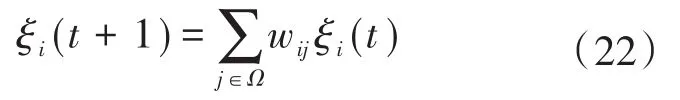
式中：ξi（t），ξi（t+1）分别为代理j在第t次迭代后的局部信息以及代理i在第t+1次迭代后的局部信息；Ω为在整个信息交互过程中所涉及的总代理数；wij为代理i与代理j间的通信系数。

各代理i的优化步骤如下：

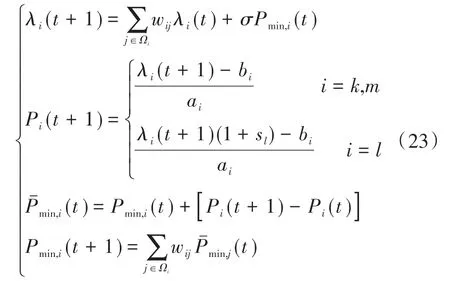
式中：Pmin，i（t）表示整体供给和需求失配量的局部估计；λi（t+1）为在进行第t+1次迭代时，代理i的边际成本；Ωi为和代理i之间相连接的代理索引；σ为能够调整收敛速度的步长。

如果σ的值足够小，通过该一致性算法建立的系统能够不断调整，直至收敛。当在λi（t）收敛至最佳结果λ*，局部估计值Pmin，i（t）将降为0，从而达到功率平衡约束条件，该算法框图如图4所示。

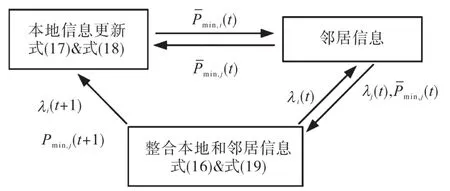
图4 代理算法的框图Fig.4 Block diagram of agent algorithm

4 算例仿真及其分析

4.1 构建仿真模型

针对IEEE-14节点系统进行调整，作为算例的仿真系统，具体如图5所示。其中，设立了9个负荷节点、1个储能节点、1个风力发电机以及4个传统发电机。

图5 仿真系统及其通信拓扑Fig.5 Simulation system and its communication topology

系统中的风力发电机的可用功率曲线如图6所示。从图6中可以看出，当时间在650～900 min时间段内，其可用功率最低。

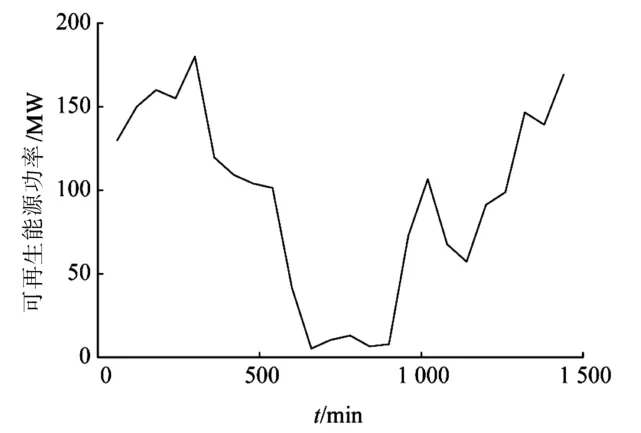
图6 风电功率曲线Fig.6 Wind power generation

系统中的各个电源、负荷、储能等参与主体的详细参数如表1所示。表1中，参数G表示传统发电机；参数B表示储能装置；参数L表示负荷；参数W表示风力发电机；参数a，b，c则对应第2节所述的各成本函数中数值。

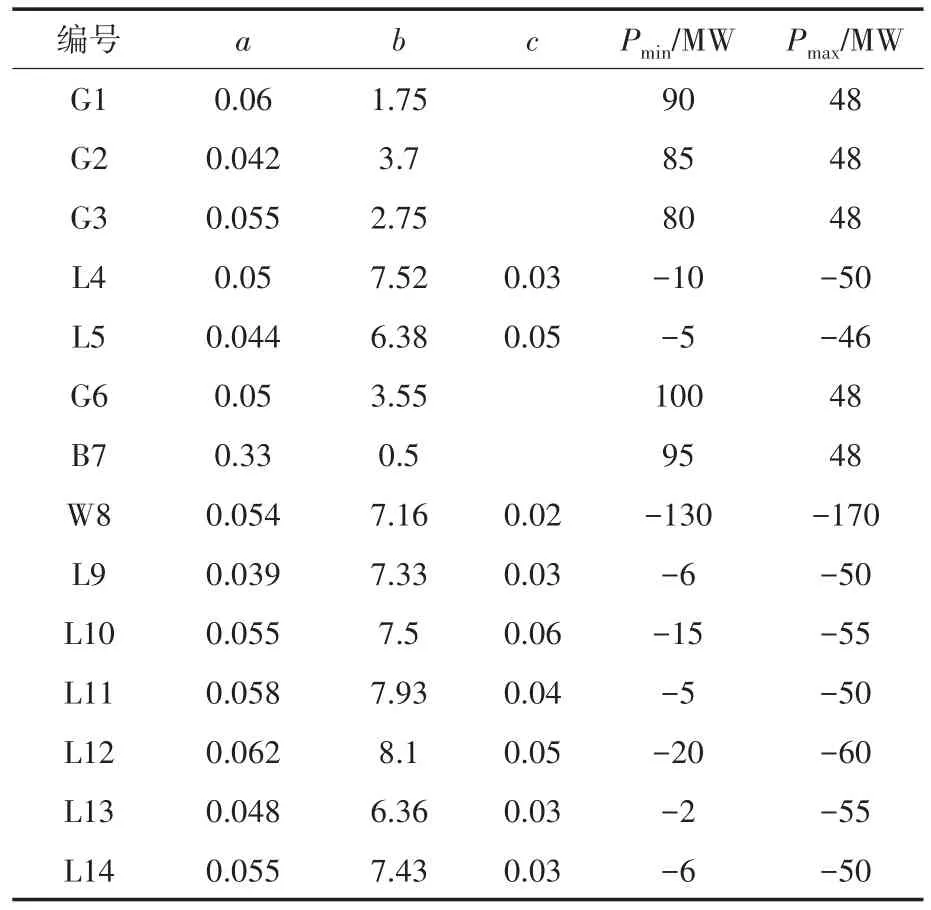
表1 仿真系统的参数设定Tab.1 Parameter setting of simulation system

4.2 弹性负荷进行协同控制

在系统的系统控制中有弹性负荷参与，能够利用负荷的响应特性，根据系统边际成本的改变对用电状态进行相应调节，进而提高风电的消纳，增大整体效率。负荷参与协同时系统中各发电的及储能装置的出力情况如图7所示，系统中各节点边际成本如图8所示。

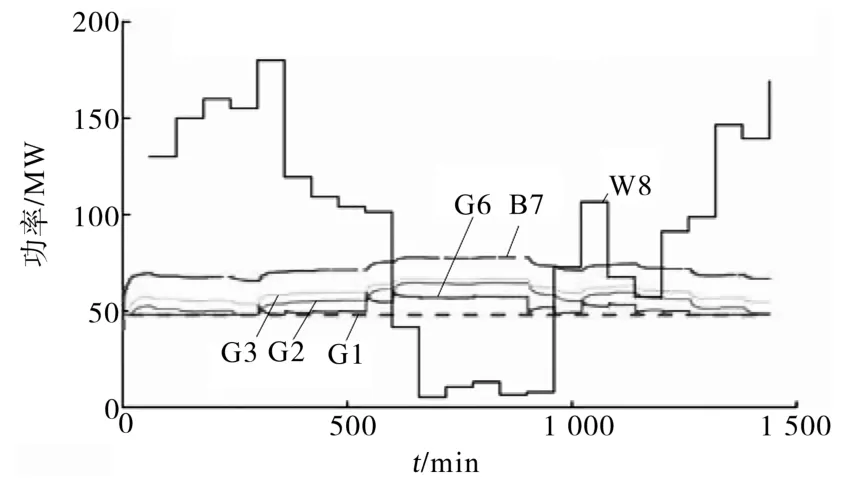
图7 负荷进行协同控制时系统出力情况Fig.7 System output during load cooperative control

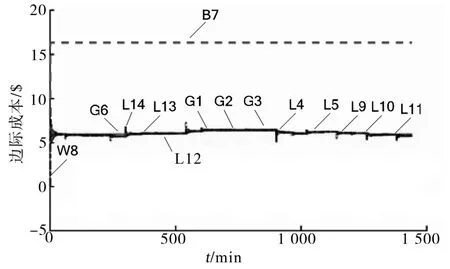
图8 负荷进行协同控制时节点边际成本Fig.8 Marginal cost of nodes during load cooperative control

通过对比图7、图8可以发现，风电出力与系统边际成本呈负相关，传统发电机组则在系统边际成本比较高的时候加强对应的电出力，从而得到最多的收益，所以传统机组出力变化和边际成本变化情况变动趋势基本一致。

对负荷侧进行分析，其负荷的功率变化情况如图9所示，其中负荷值取数值的绝对值。

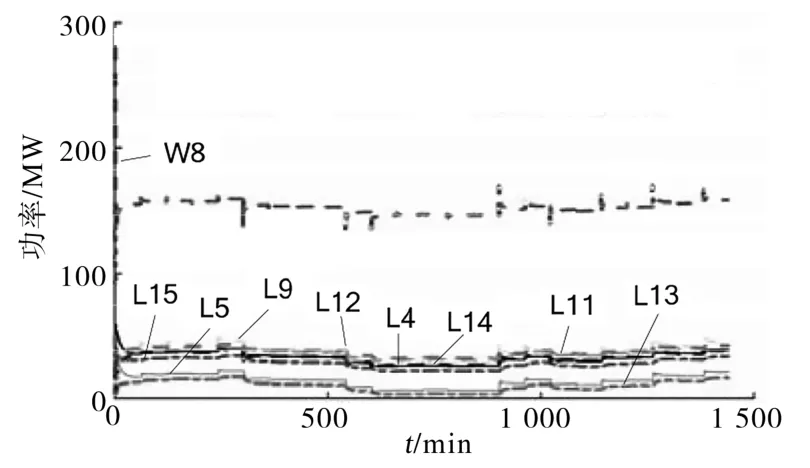
图9 负荷的功率变化情况Fig.9 Power variation of load

从图9中能够看出，系统边际成本对用户用电成本造成直接影响，在边际成本较低的阶段内，可调负荷会有所增大，进而补偿在高边际成本阶段所降低的负荷。即当边际成本降低的情况下，负荷将会加大消耗量，反之，在边际成本上升的情况下，负荷将会降低使用量。负荷参与协同作用下，系统供求不平衡量估计如图10所示。

图10 负荷进行协同控制时系统功率不平衡量Fig.10 System power unbalance during load cooperative control

从图10中得到，通过协同控制，系统的源功率和负荷功率最终能够达到平衡状态。

4.3 弹性负荷不参与协同控制

弹性负荷不参与协同时各机组和储能的出力变化如图11所示。

图11 负荷不参与协同控制时各机组和储能的出力变化Fig.11 Output change of each unit and energy storage without load cooperative control

从图11中可以看出，在60～300 min和1 320～1 440 min的时间段内，各机组和储能的出力达到下限，此时系统需要采取弃风限电措施，系统总体灵活性降低，造成弃风现象，能源有效使用率降低。

相对应的负荷不参与协同控制时的风电功率输出变化如图12所示。从图12中能够看出，在，60～300 min和1 320～1 440 min的时间段内，其风电功率输出均未达到其输出上限。由此表明了负荷不参与需求响应情况下，系统吸纳风电的能力大大降低。

图12 负荷不参与协同情况下风电功率输出情况Fig.12 Wind power output without load cooperative control

负荷不参与协同时的节点边际成本如图13所示，从图13中能够看出，一旦系统出现了弃风限电措施，其传统发电机和储能装置各节点的边际成本就出现了变化，不再是完全一样的了。

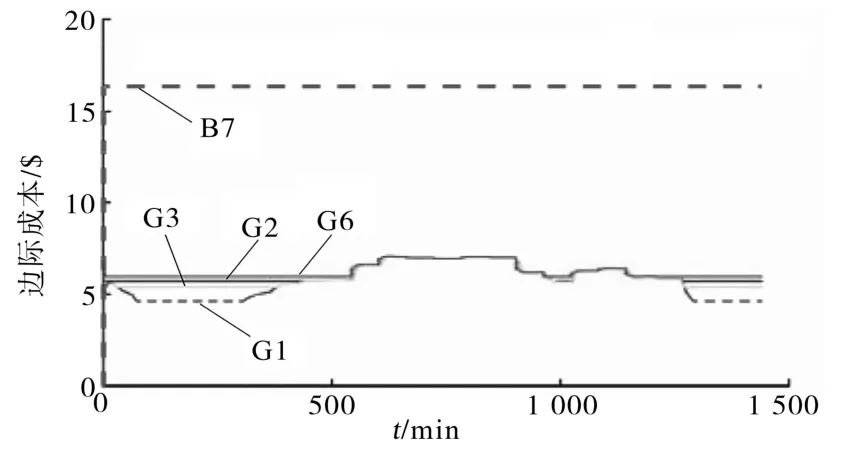
图13 负荷不参与协同控制时节点边际成本Fig.13 Parginal cost of modes without load cooperative control

负荷不参与协同情况下系统供求不平衡量估计如图14所示。图14中表明了该系统的供求达到平衡，其算法收敛。

图14 负荷不进行协同控制时系统功率不平衡量Fig.14 System power imbalance without load cooperative control

4.4 复合算法与传统算法对比分析

为了验证该所提的复合算法方法的有效性，将其结果与传统的粒子群算法的结果进行对比分析，如表2所示。从结果可以看出，两种算法的结果十分接近，最大误差仅0.0645%，从而表明该复合算法的计算结果具有一定可靠性。

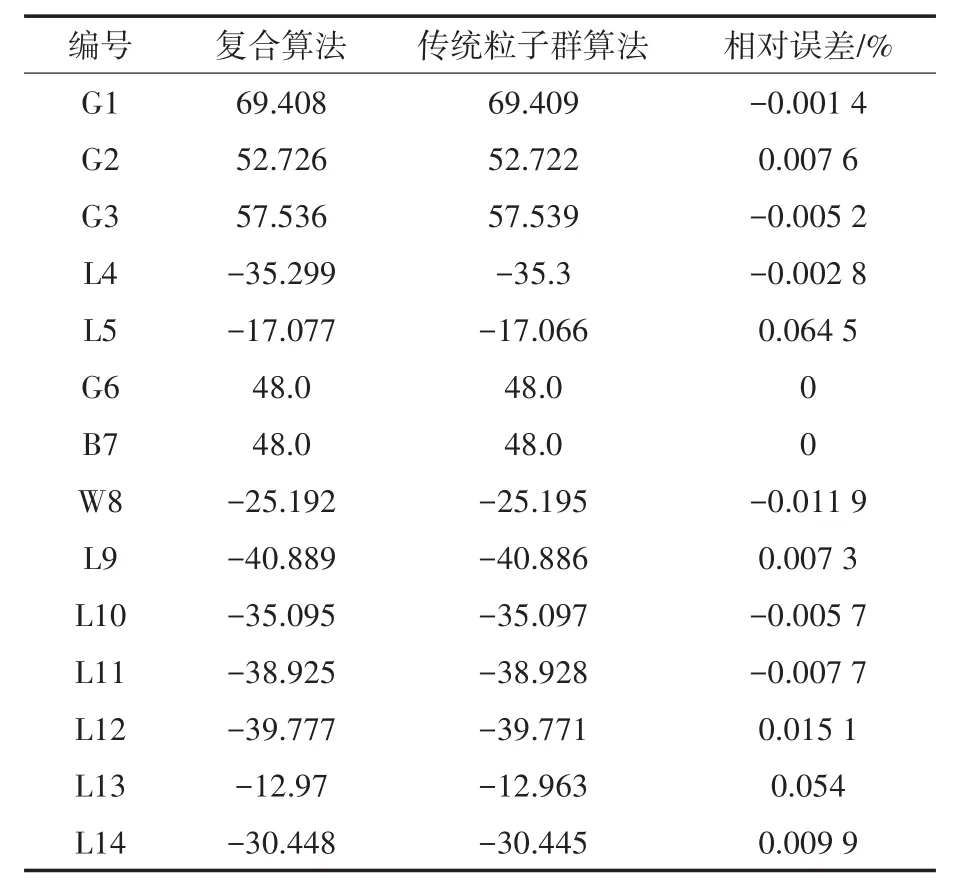
表2 计算结果对比Tab.2 Comparison of calculation results

将该复合算法与传统的粒子群算法收敛速度展开比较，其迭代次数如图15所示。从图15中可以得到，两种方法的最终收敛结果一致，然而传统算法在迭代30次后收敛为稳定，而复合算法仅用18次就达到了稳定状态。从而得出两种方法收敛精度一样，复合算法的收敛性能更佳，速度更快。

图15 复合算法与传统算法的收敛情况Fig.15 Convergence of compound algorithm and traditional algorithm

5 结论

本文研究了基于模糊智能算法和一致性算法的“源-网-荷-储”协同控制策略。通过考虑可再生能源输出的不稳定性以及弹性负荷反馈特征，构建了“源-网-荷-储”系统的最佳协同优化模型。利用将模糊算法引入粒子群算法中，再与一致性算法相结合的混合策略对系统的最佳协同优化模型展开解析。其结果表明，通过利用该复合智能算法对系统协同控制，不仅能够显著增大可再生能源的消纳率，还能根据成本信号有效提高负荷进行需求响应。此外，所提出的基于模糊与一致性复合智能算法具有跟传统粒子群算法一样高的计算精度，且比传统的粒子群算法具有更快的计算速度，其收敛次数仅仅约为传统粒子群算法的1/2，大大提高了运算效率。该方法在实时性要求较高的动态电力系统控制中具有一定普适性。