基于弹塑性损伤-渗流耦合模型的隧道洞口段围岩稳定性研究

2021-09-09万友生

中国安全生产科学技术 2021年8期

万友生

(南昌轨道交通集团有限公司，江西南昌 330013)

0 引言

隧道洞口段一般具有埋深较浅、围岩质量差、偏压作用明显等特点，因此在开挖过程中容易失稳，发生工程事故。对此，相关学者对隧道洞口段的开挖稳定性问题展开研究。张惠民[1]利用FLAC软件分析不同埋深和支护方式对隧道洞口段围岩和支护结构的稳定性；宋洋等[2]通过数值模拟和分析现场监测数据的方法指出施工过程中的重点巩固部位；皇民等[3]利用数值模拟和模型实验研究地震对洞口段工程稳定性的影响规律；杨佳奇等[4]总结寒区隧道洞口段工程稳定性的影响因素，并引入模糊评判的方法，对其进行风险评估；郑明新等[5]利用强度折减法分析钢花管注浆在洞口段隧道施工中的加固效果；郭小红等[6]通过归纳工程资料，总结出洞口段隧道洞内塌方和边坡失稳的10大致灾因素；任洋等[7]通过离心台实验对强震作用下的隧道洞口段动力响应特征和规律展开研究。

岩土工程中，隧道工程开挖产生的应力重分布作用会使周围岩体中的裂隙、孔洞等微缺陷发育贯通，形成损伤[8-9]。损伤的存在会使岩石宏观力学性质如弹性模量、单轴抗压强度等发生弱化，威胁施工安全。同时，力学场的变化使得岩石骨架结构发生变化，裂隙等的贯通进一步加剧地下水的渗流作用，改变孔隙水压分布规律，通过有效应力原理反作用于岩石力学场。因此，在施工设计时还应充分考虑应力-渗流的耦合作用。

现有研究中，针对孔隙水渗流作用下的边坡或隧道单一结构类型的稳定性研究较多[10-12]，但针对隧道洞口段这一边坡-隧道复合结构的相关研究报道较为少见,且研究过程中均未考虑到岩石的荷载损伤问题。对此，本文建立基于Morh-Coulomb(M-C)准则的岩石弹塑性损伤-渗流耦合模型，基于完全隐式的向后欧拉积分算法编写应力求解程序，并通过ABAQUS的子程序接口实现应力-损伤-渗流的完全耦合计算；以福建某在建隧道为工程依托，建立三维有限元计算模型，分析降雨渗流作用对洞口段边坡和隧道明洞的影响规律，旨在为类似工程的安全设计，提供一定的理论依据。

1 基于M-C准则的岩石弹塑性损伤-渗流耦合模型

1.1 基于M-C准则的岩石弹塑性损伤模型

考虑损伤的M-C准则如式(1)所示：

(1)

式中：f为屈服函数；I1为应力张量第一不变量；J2为应力偏量第二不变量；θ为罗德角；φ为内摩擦角，°；c为黏聚力，Pa；ω为损伤变量。

根据相关研究给出损伤演化方程，如式(2)所示[13]：

(2)

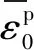
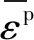
(3)

式中：εp1，εp2，εp3分别为3个主应力。

损伤变量演化规律如图1所示。

图1 不同κ值下损伤变量演化规律

此外，由Lemaitre有效应力和应变等效假设理论可知损伤材料的应力-应变关系如式(4)所示：

σ=(1-ω)Dε

(4)

式中：D为材料的弹性刚度矩阵；σ为应力矩阵；ε为应变矩阵。

损伤作用下岩体的应力应变曲线如图2所示。

图2 损伤作用下岩石应力-应变曲线

1.2 岩石应力-渗流耦合方程

由有效应力原理可知，渗流场产生的孔隙水压值对岩石应力场造成影响，如式(5)所示：

(5)

根据Kozeny-Carman公式，非破裂区岩石渗透系数可以表示为体积应变的函数，如式(6)所示：

(6)

式中：K为岩石的渗透系数，m/s。K0为初始渗透系数，m/s；n0为初始孔隙度；εv为体积应变。

对于破裂损伤区的岩体，其渗透系数如式(7)所示[14]：

K=K0·10ξ(A′e-ω/α+B′)

(7)

式中：ξ为跳突系数；A′,B′，α分别为经验参数。

2 耦合模型的数值求解算法

2.1 M-C准则的数值积分算法

由于M-C准则在屈服面上存在棱线、尖点等数值不连续特征，造成应力积分困难。为保证计算精度，摒弃角点光滑法等近似解法，从主应力空间出发，建立M-C准则的完全隐式向后欧拉算法，避免数值“奇异点”的问题。M-C准则在π平面上的图形如图3所示。

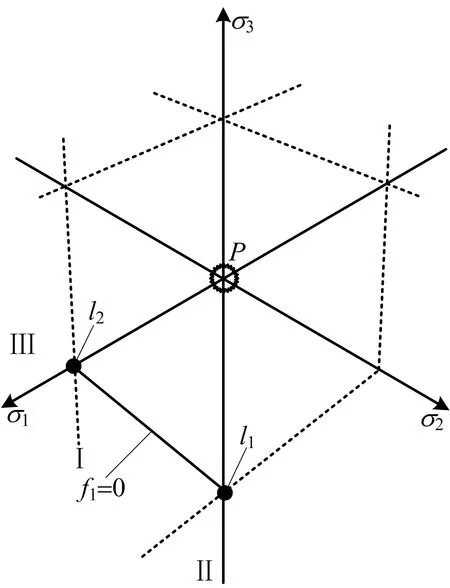
图3 M-C准则在π平面上的图形

为减少应力维数，简化计算过程，在主应力空间中对问题进行讨论。由于空间应力的对称性，只在σ1>σ2>σ3区域分析问题即可。

主应力空间中M-C准则的表达式如式(8)所示：

(8)

式中：f1～f6分别为不同应力区域内屈服函数的表达式；σ1为最大主应力；σ2为中间主应力；σ3为最小主应力。

用膨胀角ψ代替式(8)中的内摩擦角φ可得到与屈服函数具有相同形式的塑性势函数gi。

整个应力计算过程分为弹性预测、塑性修正和损伤修正3个部分：

1)弹性预测

弹性预测公式如式(9)所示：

(9)

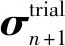
(10)

式中：σn+1为tn+1时刻的计算应力。

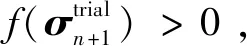
2)塑性修正

映射应力可能存在的区域为应力平面f，棱线l1或l2及尖点P处。为判断应力所在区域，利用边界面法对应力区域进行划分，边界面方程的定义如式(11)所示[15]：

(11)

(12)

(13)

(14)

(15)

(16)

式中：p为向量长度，取1；a2为f2对应力的导数。

σa的表达式如式(17)所示：

(17)

式中：k为与摩擦角有关的常数。

同理可以建立边界面方程如式(18)所示：

(18)

建立边界面后，将试算应力带入，当pⅠ-Ⅱ≥0且pⅠ-Ⅲ≤0时，应力返回至屈服面；当pⅠ-Ⅱ<0且pⅠ-Ⅲ<0，应力返回至棱线l1;当pⅠ-Ⅱ>0且pⅠ-Ⅲ>0时，应力返回值棱线l2；否则应力返回至尖点。

判定返回区域后，根据塑性增量理论，分别建立N-R方程对更新应力进行求解，更新应力表达式如式(19)所示：

(19)

式中：Δσp为塑性应力增量；Δλ为塑性因子。

3)损伤修正

塑性应变求解方程如式(20)所示：

(20)

将求得的塑性应变代入式(2)～(3)中计算损伤变量。在新求得的损伤变量基础上，对应力进行再次修正，修正方程如式(21)所示：

(21)

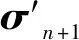
2.2 流固耦合计算流程

基于ABAQUS软件中的UMAT和USDFLD子程序接口实现流固耦合的计算过程，计算流程如图4所示。

纳入标准：①患者被本院医师诊断为输卵管妊娠；②患者的随访依从性较高；③患者自愿参与本次试验，且签署知情同意书。排除标准：①患者合并其他较为严重的疾病；②患者非自愿参与本次试验，或者未签署知情同意书。两组患者一般资料比较,差异无统计学意义(P>0.05)，具有可比性。本研究获得医院伦理委员会批准。

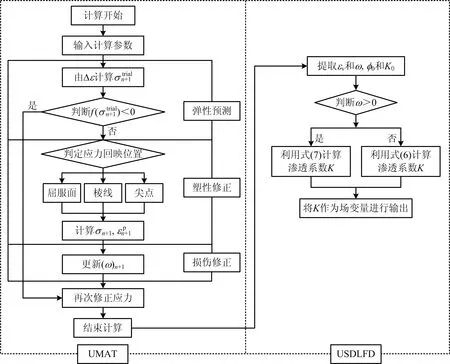
图4 流固耦合计算流程

3 洞口段计算模型

3.1 工程概况

苏桥隧道位于福建省苏桥村，为双线小净距隧道，长360 m左右，最大埋深60 m。根据现场调查和钻探揭露，所选典型断面主要地质组成由上而下主要为强风化石英砂岩和中风化石英砂砾岩。

3.2 有限元计算模型

根据苏桥隧道施工设计图纸建立有限元计算模型，如图5所示。建立的边坡数值模型中总节点数为38 622个，单元数为29 199个。设置静水位线，水位线以下孔隙水压成梯形分布。模型底部为不透水边界。坡面设置为降雨边界条件。从最不利角度出发，岩石计算参数参照Ⅴ级围岩进行选取，损伤参数κ=20，α=0.3。隧道主要支护形式为衬砌。计算参数如表1所示。

表1 洞口段模型计算参数

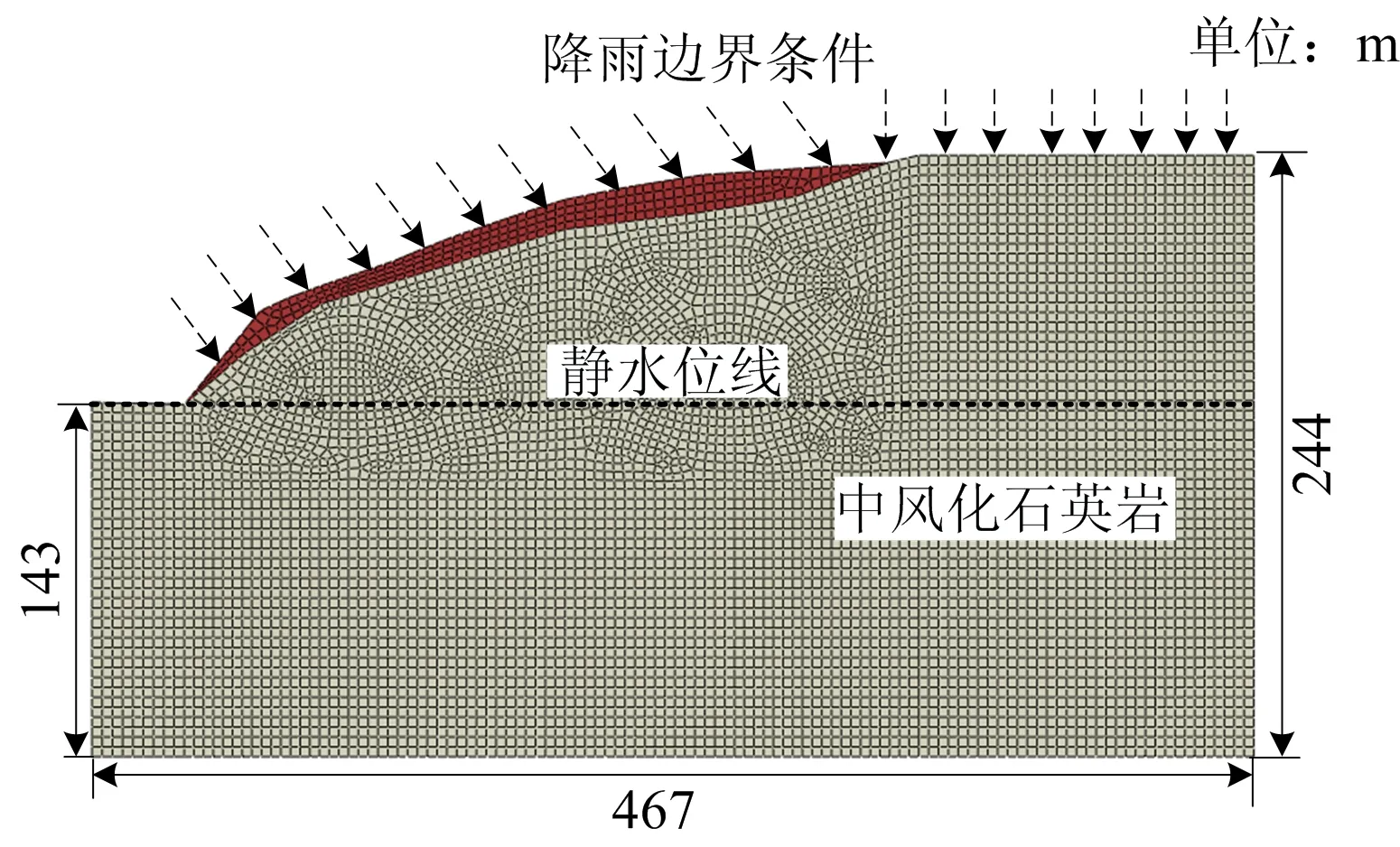
图5 有限元计算模型

依据相关文献及当地水文资料，拟定3种降雨条件分别进行计算，具体如表2所示。

表2 3种降雨类型参数

4 计算结果分析

4.1 降雨强度对复合结构安全系数的影响

利用重力加载法对不同降雨强度下的边坡安全系数进行计算，结果如图6所示。

由图6可知，在同一降雨强度下，安全系数随着降雨时间的增加而不断下降，降雨初期的安全系数变化较降雨后期剧烈，在第28 h左右安全系数逐渐趋于稳定。对于3种不同类型降雨来说，孔隙水压力变化幅度越大，边坡安全系数下降的幅度越大，大于降雨条件下的安全系数变化幅度最大为6.46%。在第48 h，3种类型降雨的安全系数从小到大排序为：大雨类型<中雨类型<小雨类型，最小安全系数为1.07。

图6 不同降雨类型下洞口段安全系数变化规律

4.2 降雨强度对隧道围岩变形规律的影响

设置降雨量分别为0.002，0.004，0.006，0.008，0.01 mm/h，降雨时长为72 h，对降雨过程中的隧道拱顶沉降、拱底隆起和拱腰收敛变化规律进行计算，结果如图7所示。

图7 不同降雨强度下隧洞变形曲线

由图7可知，降雨初期隧道内各个监测点的位移均发生明显变化。随着时间发展，土体逐渐饱和，位移变化速率逐渐平滑，最后趋近于零。降雨强度越大，最终位移值越大。由于洞口段的偏压作用，隧道左洞和右洞的位移值变化规律不同。对拱顶监测点而言，在相同降雨强度下，右洞的沉降值均要大于左洞沉降值。而左洞拱底隆起值大于右洞拱底隆起值。2洞的拱肩向不同方向收敛。

图7(a)中，对某时间段强降雨过程中拱顶位移变化监测值与计算值进行对比。由对比结果可以看出，数值计算结果在数值上略有偏差，变化规律基本一致，证明本文模型的准确性与工程实用性。

对降雨过程中(降雨量0.01 mm/h)的损伤区进行计算，结果如图8所示。

由图8可知,当降雨持续60 h后，岩体内部开始产生损伤区，损伤区范围与损伤值大小随着降雨进程的逐渐发展。塑性区发生在左洞与坡面之间，即孔隙水压最大值所在处，计算结果再次证明降雨对洞口段边坡造成的安全隐患。