基于PFC的矿石块度对溜井放矿效果的影响研究
2021-09-09李志国李国书宋金凤黄诗杰
李 贲 李志国 李国书 宋金凤 黄诗杰
(武汉工程大学资源与安全工程学院(兴发矿业学院),湖北武汉430073)
0 引言
溜井是溜井放矿开拓方式矿山的运输咽喉,其放矿效果的好坏对矿山产生影响极大。评价溜井放矿效果的好坏主要有两方面:一是放矿效率,放矿效率越高则放矿效果越好,溜井放矿效率直接影响矿山实际生产能力[1];二是矿石对溜井井壁的撞击程度,放矿过程溜井一旦发生破坏,卡矿或堵塞,不但影响矿山的正常生产,而且会对其他井巷工程的安全造成威胁[2-4]。
目前国内外普遍接受的影响放矿效果的因素有:矿石含水率、料仓几何形状、震动放矿机特性、材料物性、储矿时间和高度及矿石块度等,其中矿石块度是最重要的影响因素之一,众多学者开展了大量研究。相应的研究方法主要涉及理论计算、理论分析、相应性模拟、数值模拟方法等[5-7]。其中,PFC(颗粒流程序)是以介质内部结构为基本单元(颗粒和接触)、从介质结构力学行为角度研究介质系统的力学特征和力学响应[8-10],在该领域应用广泛。秦宏楠等[11]通过使用PFC2D简化溜放矿石冲击井壁的模型为颗粒流撞击墙的模型,以运动学理论分析结合离散元程序模拟分析了溜放矿石在井筒内的运动规律及对溜井井筒的冲击破坏规律。张慧等[12]通过使用PFC2D数值模拟实验研究了矿石块度模数对溜井放矿流动性的影响,提出了溜放矿石的块度分布特征是影响流动性的根本因素。
纵观前人研究成果,针对矿石块度对溜井放矿效果的影响评价多局限于计算单一评价指标,不能综合反映放矿效果的优劣。本项目在前人的研究基础上,基于PFC2D离散元数值模拟软件,针对大冶某矿山特定溜井参数进行数值模拟实验,研究矿石块度对于放矿矿石的流动性及对溜井井壁的撞击力的影响,构建评价放矿效果的综合评价公式,并系统分析矿石块度对溜井放矿效果的影响,研究内容对溜井放矿最优块度的选取具有理论价值和工程意义。
1 实验原理与方案设计
1.1 实验原理
1.1.1 线性接触模型基本原理
在离散元软件PFC2D中的接触本构模型有很多种,常用的几种分别为线型接触模型、平行粘结模型、接触粘结模型、滚动接触模型、Burger接触模型等。宿月文等[13]研究圆柱内接触力模型的构建方法,综合对比了8种不同的弹性接触力和耗散阻尼力模型,提出了新的适用于微间隙和低恢复系数情况的接触力模型。在此次实验中采用线性接触模型,使用线型接触模型的原因是各个矿石颗粒之间应是独立的,在计算稳态中颗粒之间应该无粘结,在重力与颗粒间相互作用力下自由下落。并通过参数继承的方法增加了颗粒—墙体,颗粒—颗粒的线性接触模型。
线性模型再现了一个无穷小的、线性弹性和摩擦界面的力学行为,它承载着点力,界面不抵抗相对旋转和可选粘性阻尼器可能被激活。图1显示了模型的简图,介绍了它的主要参数。法向力和剪切力是由线性弹簧(具有恒定刚度kn和ks)平行作用于粘滞阻尼器(具有阻尼系数n和s)的组合产生的。剪力总是通过剪切位移增量逐步累积(因此ks是切线刚度)。另一方面,法向力可以递增累加。接触活动状态和正常的力依赖于接触间隙,滑移行为是通过使用摩擦系数μ对剪切力施加库仑极限来调节的。阻尼器的行为可以通过选择阻尼器模式、Md和阻尼器临界阻尼比的值来修改。
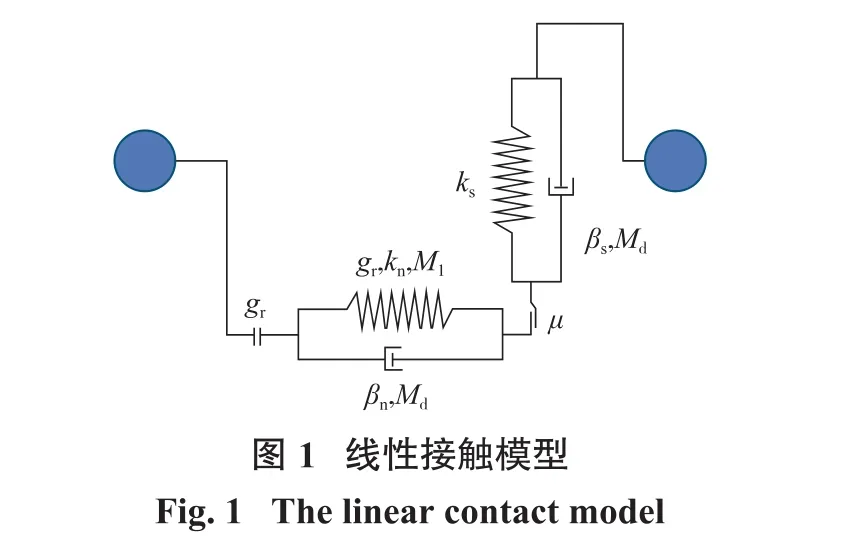
参考间隙gr定义了接触活动距离(详见接触检测部分)。接触活动是根据与当前接触间隙gc的比较来确定的,如下所示:

力—位移计算被跳过非活动接触,接触力和力矩通过以下方式更新:
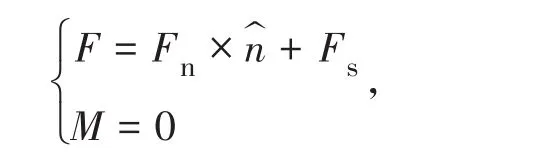
其中,下标n,s分别表示法向和剪切方向。按照惯例表示压缩。将相对平移位移增量分解为法向分量和剪切分量。当活动发生在当前时间步长的某个部分时,接触从非活动到活动的周期增量力可能无法准确计算。定义校正因子来校正此时间步内的相对位移增量:
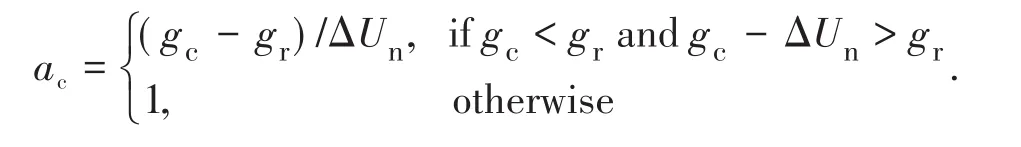
将相对位移增量(相对速度没有改变)修改为

1.1.2 放矿效果评价原理
评价溜井放矿效果的好坏主要有两方面:一是放矿效率,以单位时间内放出的矿石质量来衡量;二是井壁的撞击程度,以撞击总能量来衡量。
溜井放矿效率:

式中,F为放矿效率;M为放矿质量;t为放矿时间。在控制其他条件不变的前提下,F值越大,溜井放矿效果越好。
撞击总能量:

式中,E为矿石对井壁撞击总能量;Ni为撞击力;Xi为墙体被撞击时的形变量。在控制其他条件不变的情况下,E值越小,溜井放矿效果越好。
综合评价公式:

式中,Z为放矿效果;Z值越大则放矿效果越好;a,b分别为F、E的评价因子,与矿山实际生产与溜井参数相关。
1.2 实验方案
以大冶某矿山主溜井为研究对象建立主溜井模型,溜井参数取值见表1。以不同级配的颗粒半径代表不同矿石块度分布情况,颗粒半径级配采用高斯分布,分为5组,期望值分别取0.20 m,0.25 m,0.30 m,0.35 m,0.40 m,0.45 m,标准差取0.10 m,矿石参数值见表1。引入重力加速度取值9.8 m/s2,使矿石在自重的作用下,在井筒内与其他矿块和井壁发生一系列的相互作用,最终溜放出来。如图2所示为颗粒半径级配为r~(0.25,0.102)时的放矿过程模拟图。

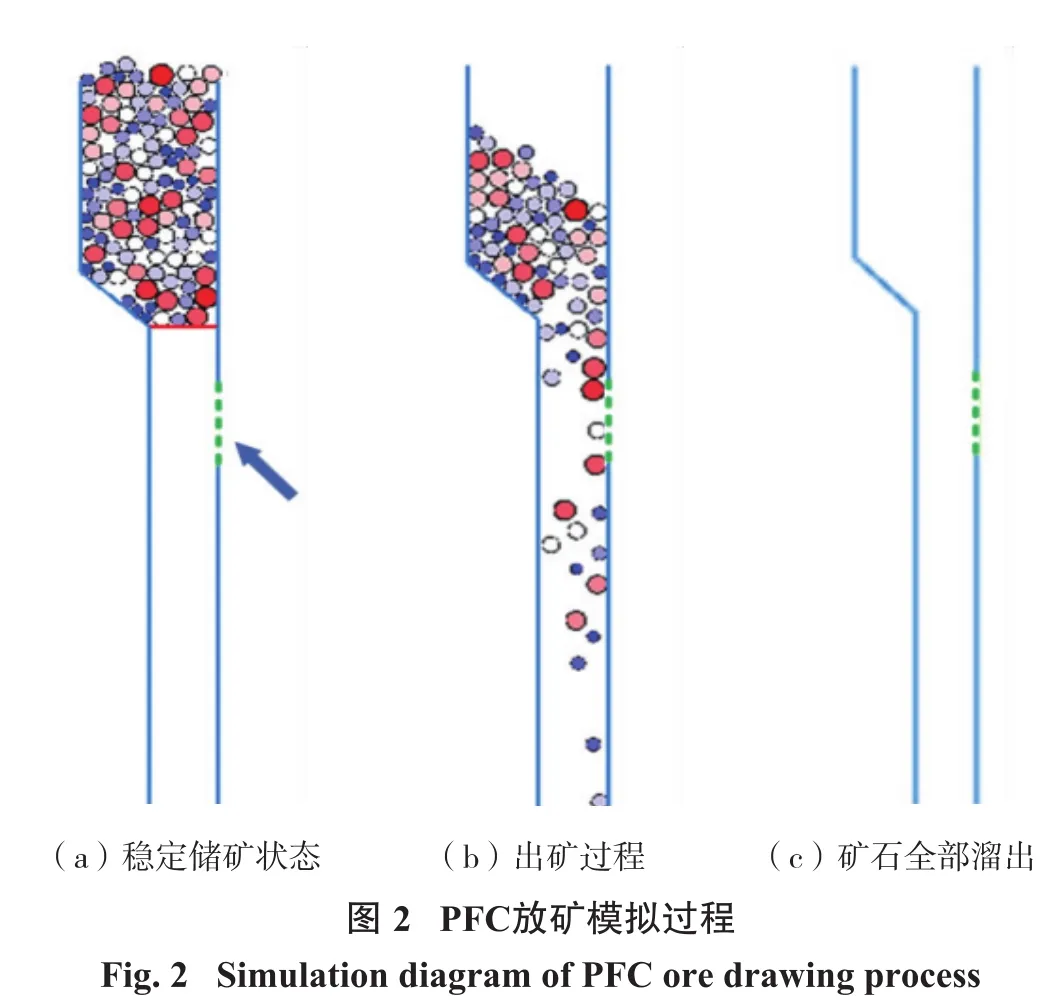
秦宏楠等[11]在基于颗粒流的溜井冲击破坏规律的研究中指出,对于百米深溜井,溜下矿石经溜槽溜出后,与溜井井壁大致经过3次碰撞即可落入井底,第二次碰撞是碰撞过程中幅度最大,频率较高的一次碰撞,对井壁造成的伤害程度最大。因此,在此次模拟放矿过程对溜井井壁的撞击实验时,只需要通过设定hist命令检测第二次碰撞的撞击力(即矿体对图2箭头指示部分的撞击力),这样就可以得到在放矿过程中不同块度的矿石对溜井井壁最容易受到破坏的位置的受力数据。
2 实验结果及分析
2.1 实验数据统计
实验过程中采用控制变量的方法,在其他各项参数都不变的情况下,改变颗粒半径期望值的大小。放矿模拟过程中记录到的实验数据如表2所示。当矿石块度的半径期望值增大到0.45 m时,放矿硐室发生了卡矿的现象,如图3所示。因此,对于大冶某矿山来说,放矿时的矿石块度半径期望值必须小于0.45 m。
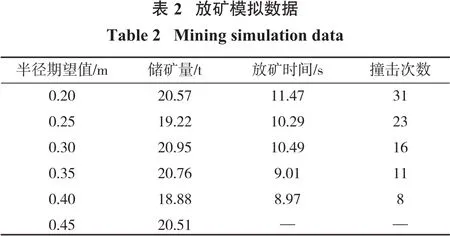

2.2 放矿效率实验结果
将实验数据代入式(1)中,可以得到不同块度大小的矿石的放矿效率,通过最小二乘法选取幂函数、指数函数以及对数函数进行拟合,分别比较其方差,得到幂函数拟合结果的方差最小。根据所得数据,按照幂函数拟合,绘制出块度—放矿效率曲线图如图4所示。
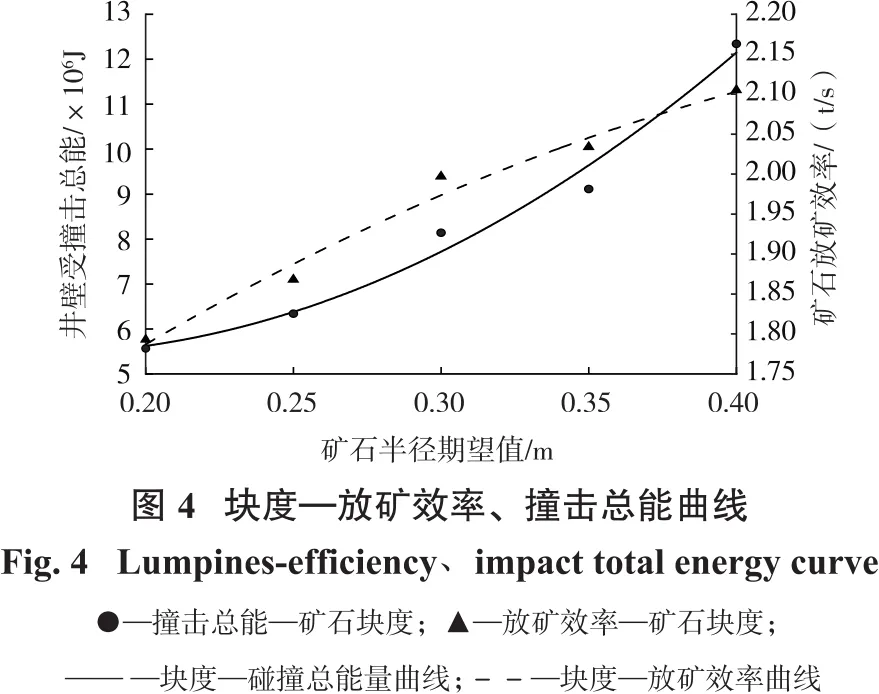
根据图4,块度—放矿效率拟合曲线:
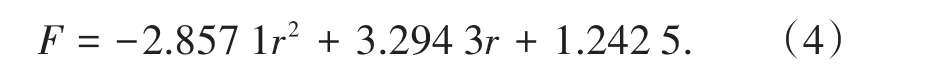
2.3 放矿撞击力实验结果
将实验数据代入式(2)中,可以得到每一次放矿过程中,不同块度的矿石对图2所示的箭头指示部分井壁产生的撞击总能量,通过最小二乘法选取幂函数、指数函数以及对数函数进行拟合,分别比较其方差,得到幂函数拟合结果的方差最小。根据所得数据按照幂函数拟合,绘制出块度—撞击总能曲线如图4所示。
根据图4,块度—撞击总能拟合曲线:
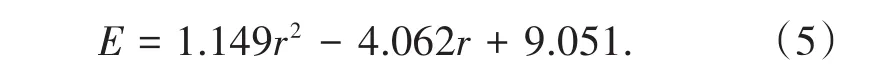
2.4 实验结果分析
由图3可知,当矿石半径期望值增大到0.45 m时,发生了卡矿的现象,因此,对于溜井的放矿流速只考虑半径期望值为0.20~0.40 m范围内的矿石。由图4可知,随着矿石块度的增大,放矿效率也随之增大,且增速越来越缓;随着矿石块度的增大,对井壁的撞击总能量也越大,且增速也越来越大。
为了更好比较出放矿效果最好的矿石块度范围,结合大冶某矿山实际情况,取a=1,b=5;将式(4)、式(5)代入综合评价式(3)中:
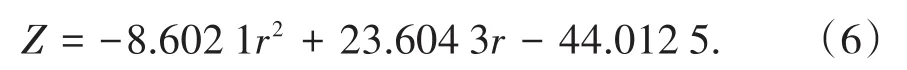
式(6)函数图像如图5所示。
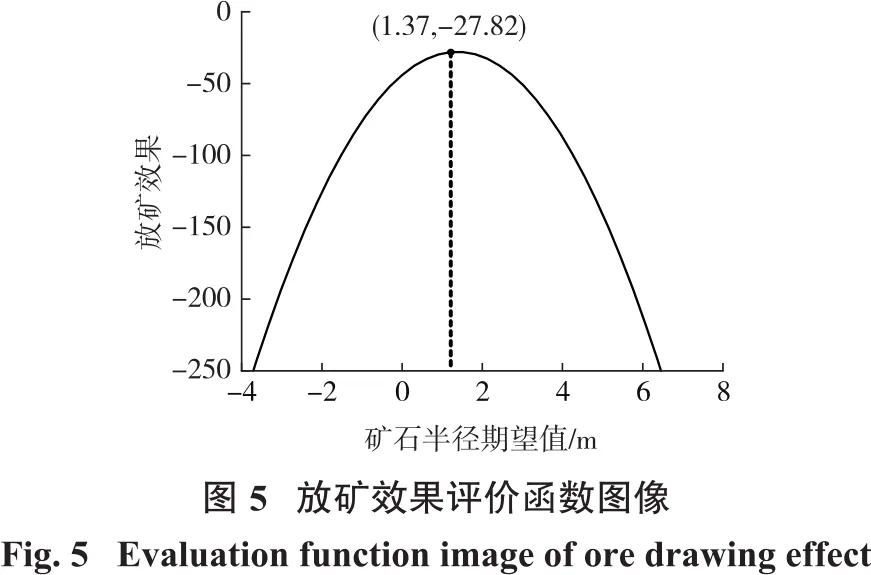
Z为二次函数,开口向下,其对称轴为r=1.37,即矿石半径期望值在0.20~-1.37 m的范围内,放矿效果随着矿石块度的增大而变得更好。按照矿山生产实际控制矿岩的最大块度为放矿口半径的1/5,即rmax≤0.45 m,这与实验中矿石半径的期望值超过0.45 m会发生卡矿的现象相契合,验证了溜井放矿效果综合评价模型的有效性。因此综合以上数值模拟实验结果以及评价模型的计算结果,大冶某矿山放矿的矿石半径分布为r~(0.40,0.102)时,放矿效果最好。
3 结论
(1)以单位时间内放出的矿石质量和撞击总能量为表征,构建溜井放矿效果综合评价模型,以综合评价放矿效率及井壁的受撞击程度。仿真结果表明,该综合评价模型能够有效描述溜井放矿过程中矿石块度对放矿效果的影响。
(2)数值模拟结果表明,随着矿石块度的增大,放矿效率会得到提高,但同时对于井壁所造成的损伤也会增大,且当矿石块度增大到一定程度,会发生卡矿现象。根据大冶某矿山的实际生产与溜井参数设定评价因子,应用综合评价模型,给出该矿山溜井放矿最优矿石块度半径分布为r~(0.40,0.102),与矿山生产实际相符。
(3)溜井放矿效果综合评价模型结构简单、计算方便,为溜井放矿效果现场评价提供了简单、有效的技术手段。
