基于GPU并行的厦门附近海域潮波传播数值模拟研究
2021-09-09孟江山路川藤罗小峰
孟江山,路川藤,罗小峰,丁 伟
(1.中交广州航道局有限公司,广东 广州 510000;2.南京水利科学研究院,江苏 南京 210029;3.河海大学,江苏 南京 210024)
1 研究背景
厦门周边海域岛屿众多,潮汐汊道交错,水流运动较为复杂。厦门海域潮汐属于正规半日潮[1],潮波主要受来自台湾海峡的潮波传播影响,水动力强度相对较弱,且主要由潮汐作用引起[2]。由于厦门附近海域近年来围垦较多,因此众多学者研究厦门海域潮流泥沙运动较多,而系统性的潮波传播研究成果相对较少,如谢森扬[3]、陆荣华[4]均系统研究了厦门历史围填海的水动力、水环境问题,许婷[5]、陈纯等[6]还针对具体工程问题研究了局部海域水沙环境问题。潮波传播理论体系目前已相对成熟[7],研究方法以实测资料分析和数学模型模拟两种手段为主,实测资料分析以调和分析[8-9]、神经网络[10]等方法为主,数学模型模拟可以弥补实测资料时段短及区域覆盖面局限等缺点,因此被广泛应用[11-12],近年来,随着计算机科学的发展,数学模型计算正朝着高分辨率、高计算效率方向发展[13],特别是GPU(Graphics Processing Unit)并行计算,大幅度节省了数学模型的计算时间,使得数学模型可以快速实现精细化、实时化模拟预报,如龚佳辉等[14]在城市雨洪模拟中,认为GPU并行可提速23.88~158.72倍。本文在前人研究的基础上,采用GPU并行算法模拟厦门周边海域潮波传播,深入研究厦门附近海域潮波传播特征,为相关工程建设和规划提供技术支撑。
2 GPU并行算法
2.1 离散方法 数学模型采用具有自主知识产权的数值模拟系统CJK3D-WEM计算,该系统于2014年取得国家软件著作权登记,适用于江河湖泊、河口海岸等涉水工程中的水动力、泥沙、水质、温排和溢油模拟预测研究。
对于水平尺度远大于垂直尺度的河口海岸地区,通过一定的假设条件(均质不可压、静压、刚盖、Boussinesq等假定),沿水深方向积分取平均,可得到平面二维水动力方程:
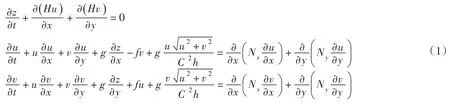
式中:H为总水深,m;z为水位,m;u、v流速矢量V沿x、y方向的速度分量,m/s;t为时间,s;f为科氏力,s-1;g为重力加速度,m/s2;Nx、Ny为x、y向水流紊动黏性系数,m2/s;C为谢才系数。
控制方程式(1)向量形式可表示为:

其中:
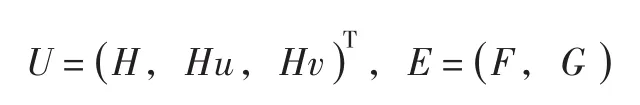
其中:
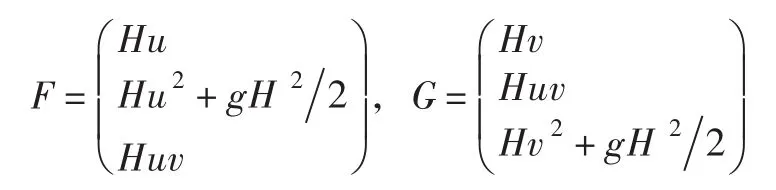
紊动扩散项:
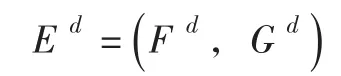
其中:
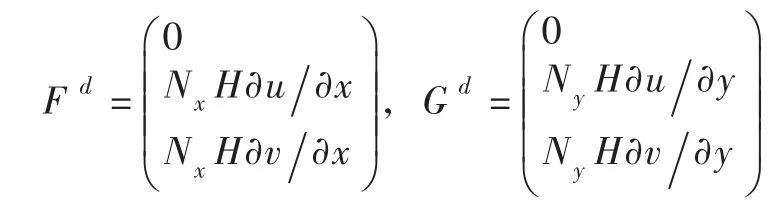
源项M表示为:
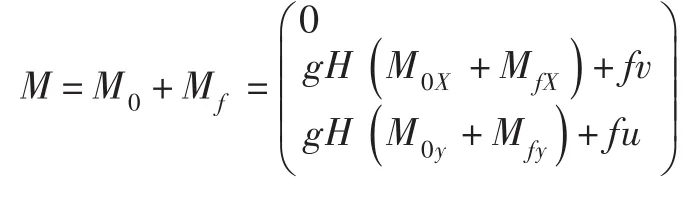
式中:Mox、Moy分别为x、y方向的河床底部高程变化;Mfx、Mfy分别为x、y方向的底摩擦项。
采用三角形网格作为控制单元,水深布置在网格顶点,其他物理变量配置在每个单元的中心。将第i号控制元记为Ωi,在Ωi上对向量式的基本方程组(2)进行积分,并利用Green公式将面积分化为线积分,得:
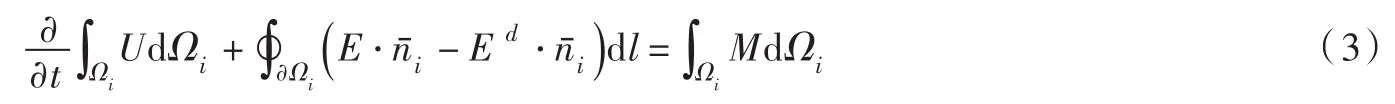
式(3)求解主要分三部分,一为对流项求解,二为紊动项求解,三为底坡项处理。对流项的数值通量采用Roe格式的近似Riemann解,紊动项采用单元交界面的平均值,计算通过该界面紊动黏性项的数值通量,底坡项采用斜底方法处理。
式(3)中对流项可表示为:
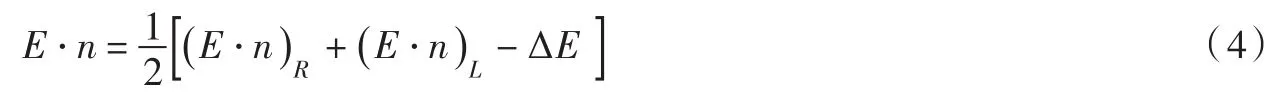
(E⋅n)R和(E⋅n)L分别为交界面两侧的数值通量,可表示为:
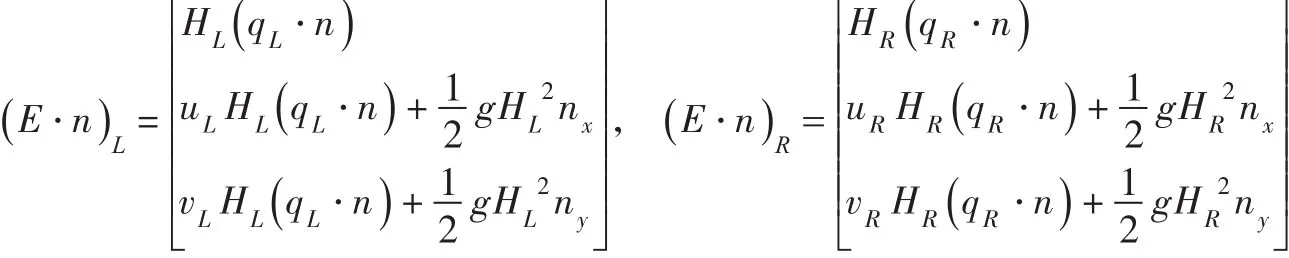
其中:
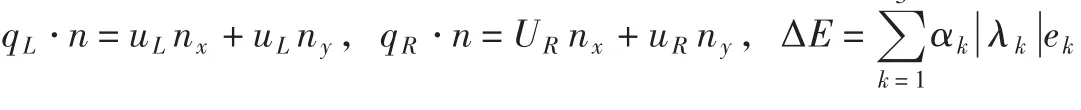
这里λk和ek(k=1,2,3)分别为对流项特征矩阵A的特征值和特征向量,满足:ΔE∗=AΔU ,特征矩阵形式如下:
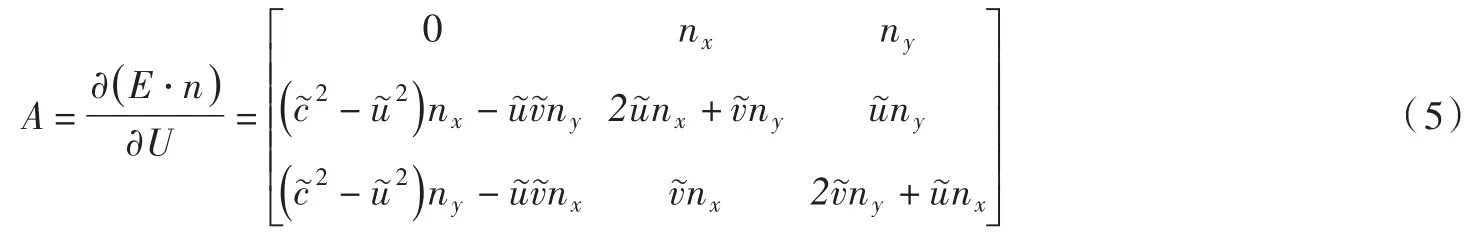
矩阵中的u͂、v͂和c͂分别采用质量加权平均计算,表达如下:
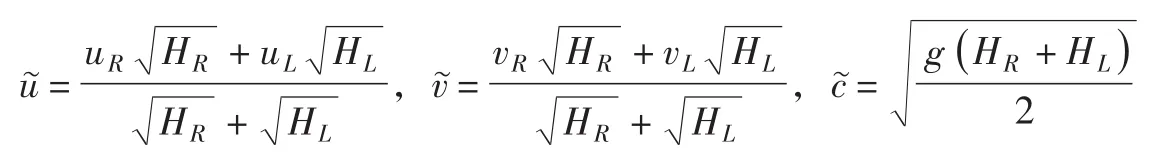
矩阵A的特征值和特征向量均可计算得出,见文献[15]。
水平扩散项含有二次项,是离散浅水方程的难点之一。本文采用单元交界的平均值计算通过该界面扩散项的数值通量,这样处理算法简单、效率高。式(3)中的水平扩散项可表示为:
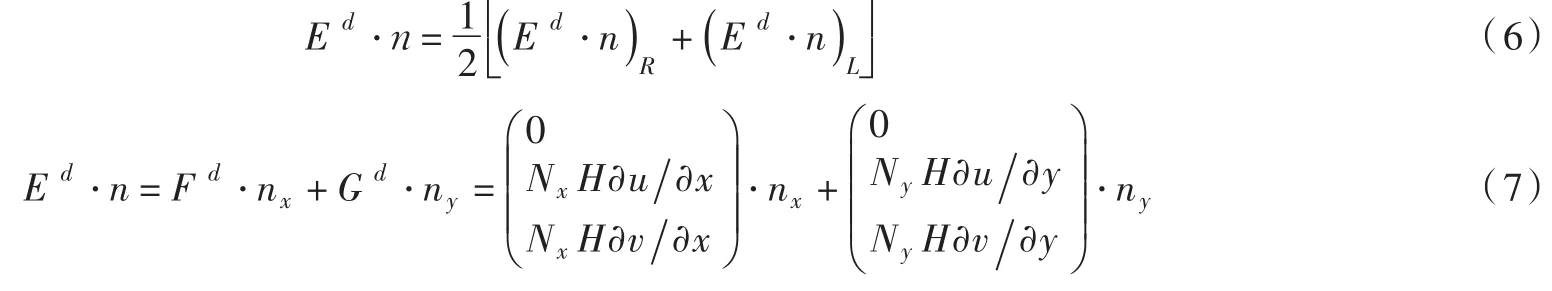
对于上式的偏导数可用如下方式求解:
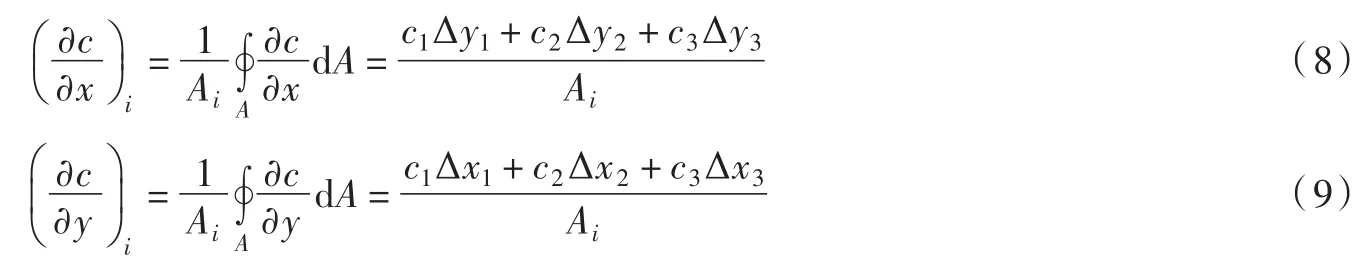
底坡项采用斜底模型求解,记某个控制体三个顶点坐标为xi,yi,zi(i=1,2,3),三个顶点按逆时针方向排序,由这三个顶点确定的平面方程为:

其中:
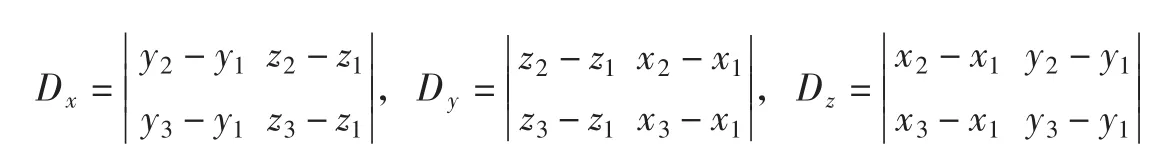
其中:当Dz≠0时,
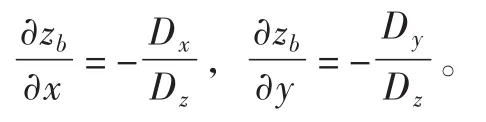
2.2 GPU并行计算 并行计算是指同时使用多种计算资源解决计算问题的过程,是提高计算机系统计算速度和处理能力的一种有效手段。目前,流体力学并行计算一般基于CPU和GPU两种手段,CPU单核计算能力强,但核心数量较少,从而限制了并行计算能力,GPU虽单核计算能力差,但核心数量多,因此并行计算效率较CPU强。
GPU并行计算程序基于CUDA架构下的C语言编写,采用单精度算法。GPU并行计算流程见图1,当CPU计算参数通过cudaMemcpy(dev_input,input,sizeof(int),cudaMemcpyHostToDevice)函数传递给GPU后,GPU通过核函数kernel实现大量并行执行线程,从而达到并行计算的效果,GPU计算结果通过cudaMemcpy(result,dev_result,sizeof(int),cudaMemcpyDeviceToHost)函数反馈给CPU,需要说明的是CPU与GPU之间的数据交换耗时较长,因此实际计算过程中应尽量降低二者之间的数据交换频率,以过丘流算例为例进行说明,计算采用的CPU型号为E5-1630V4CPU(8核心),GPU型号为NVIDIA Ge⁃force RTX2080(2944核心)。
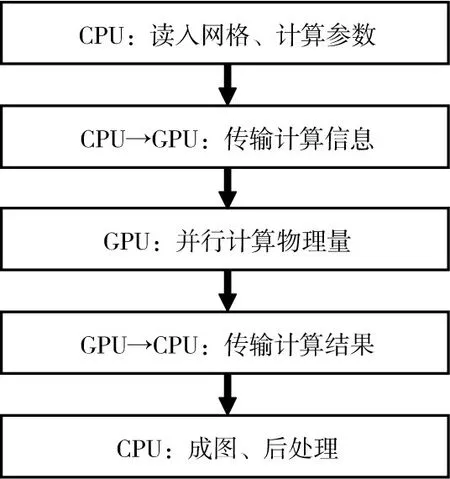
图1 GPU并行计算流程图
建立了长60 m,宽6 m的数值水槽,以三角形单元划分网格,网格总数约为20 000个,空间步长最小约为0.13 m,模型范围与地形等见图2(a)和图2(b),不考虑紊动黏性系数,模拟有激波条件下的过丘流,水槽上游径流取0.18 m3/s,下游水位-0.07 m,模拟时间1 h,由于控制方程离散格式为显式,时间步长受Courant数约束,因此时间步长取值0.003s,需运行1 200 000次循环方可完成模拟。图2(c)为CPU单核(单精度)与GPU并行(单精度)计算结果与解析解的对比,计算精度一致。图3为GPU并行计算过程中,GPU与CPU之间的数据交换频次对耗时的统计,当采用CPU单核进行计算时,计算用时约36 h,若GPU并行计算过程中,GPU与CPU之间实时(即每步)进行数据交换,则计算效率严重降低,耗时超过72 h,随着GPU与CPU数据交换频次的降低,计算时间呈指数下降趋势,当GPU每模拟15 s(5000步)与CPU数据交换1次后,计算耗时趋于稳定,约为11~12 min,与CPU单核计算相比,计算效率提高约180倍。
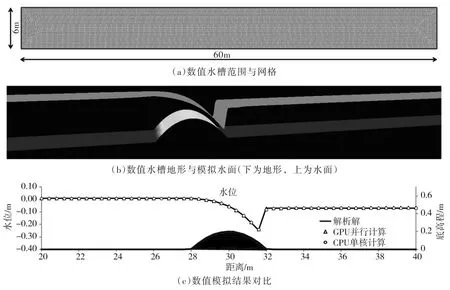
图2 有激波的过丘流数值模拟
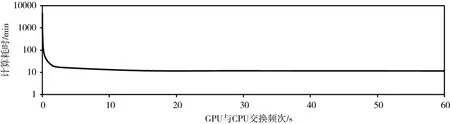
图3 GPU并行计算效率统计
3 厦门海域数学模型
3.1 研究范围与模型参数 厦门海域数学模型范围如图4所示,包括同安湾、九龙江口、围头湾等厦门岛及周边水域,模型北侧边界至泉州市崇武镇,南边界至漳州市东山县北侧,模型总长约178 km,宽约105 km。外海边界采用潮位控制,由全球潮汐预报模型Nao-test计算。模型网格总数为157 818个,工程水域网格加密,见图4,最大网格边长1825 m,最小网格边长30 m,模型水深采用2019年最新电子海图数据。数学模型时间步长取1 s,糙率采用附加糙率0.013+0.012/h(h表示水深,当h小于1 m时,糙率取0.015),紊动黏性系数采用0.1hU*计算(U*为摩阻流速)。
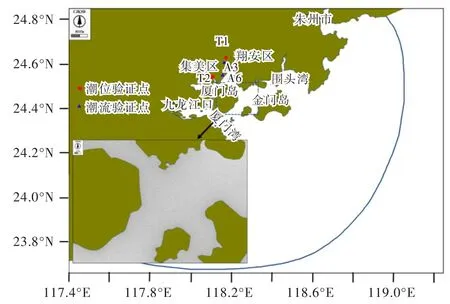
图4 数学模型范围及网格示意图
3.2 模型验证 模型采用2019年3月22—23日同安湾大潮同步水文测验资料和2019年国家海洋信息中心厦门站潮汐表资料作为模型验证资料,验证点位置见图4。图5和图6为2019年3月大潮潮位验证,图7和图8为对应的潮流验证。由图5—图8知,潮位计算值与实测值吻合较好,高低潮位偏差基本在0.1 m之内,流速和流向实测值和计算值吻合亦较好。
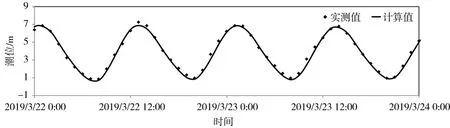
图5 T1站潮位验证
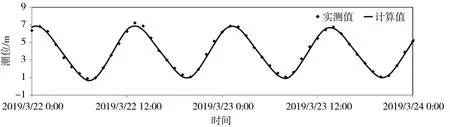
图6 T2站潮位验证

图7 A3站潮流验证

图8 A6站潮流验证
图9为厦门站2019年全年潮汐表潮位验证,采用GPU并行计算2019年全年的潮波传播过程共耗时约30 h,GPU每模拟30 min与CPU数据交换1次,采用CPU单核计算,耗时约5475 h,计算效率提高约180倍。对于长时序验证,可用Skill值表达模型验证质量,Skill值计算见式(11),当Skill值为1时,模型验证完美,Skill值越小,计算偏差越大,本文厦门站潮位统计Skill值为0.926,说明数学模型计算的厦门附近海域潮波传播相似性较好。
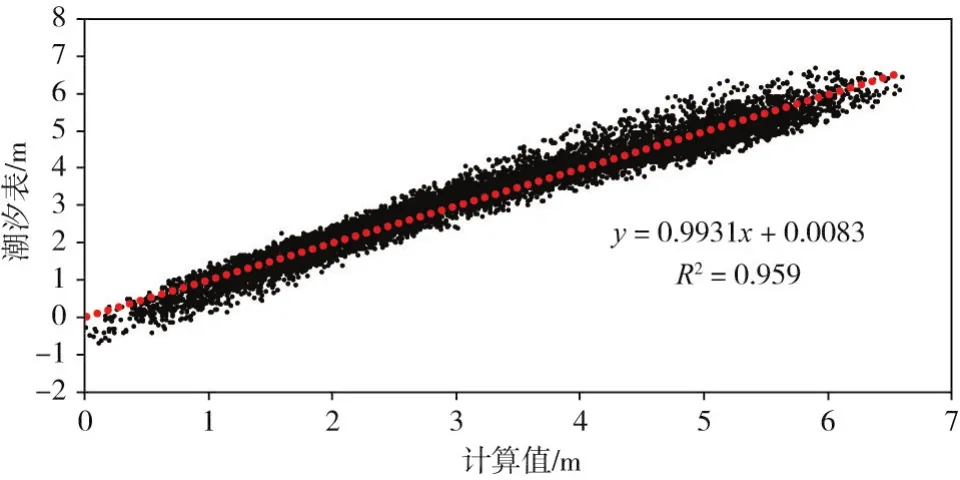
图9 厦门站潮汐表潮位验证
式中:Xmod为模型值;Xobs为观测值(本文为潮汐表预报值);为观测平均值。
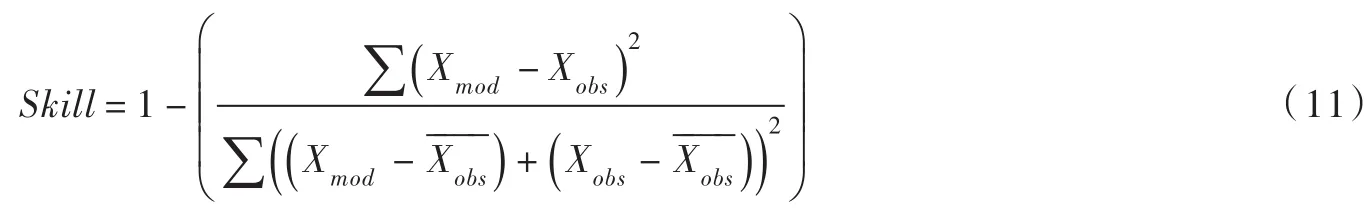
4 潮波传播空间分布特征
4.1 汊道潮流特征 厦门周边海域岛屿众多,地形边界相当复杂,涨落潮流在不同区域存在时间或者空间的不平衡。涨潮时(图11(a)),外海水流自围头湾和厦门湾两个口门向厦门岛方向运动,厦门湾口门处的涨潮流运动至金门岛西侧时,在厦门岛的阻水作用下,水流分为向九龙江口和同安湾两个方向的水流,向同安湾方向的水流与围头湾的涨潮流在厦门岛东北侧汇合,进而向同安湾运动。落潮时(图11(b)),同安湾的水体自厦门岛东西两侧向外海运动,金门岛北侧由于水深相对较浅,大部分落潮流向围头湾运动,小部分向烈屿乡方向运动,九龙江口的落潮流在厦门岛西南侧与同安湾的落潮流汇合,并向外海运动。
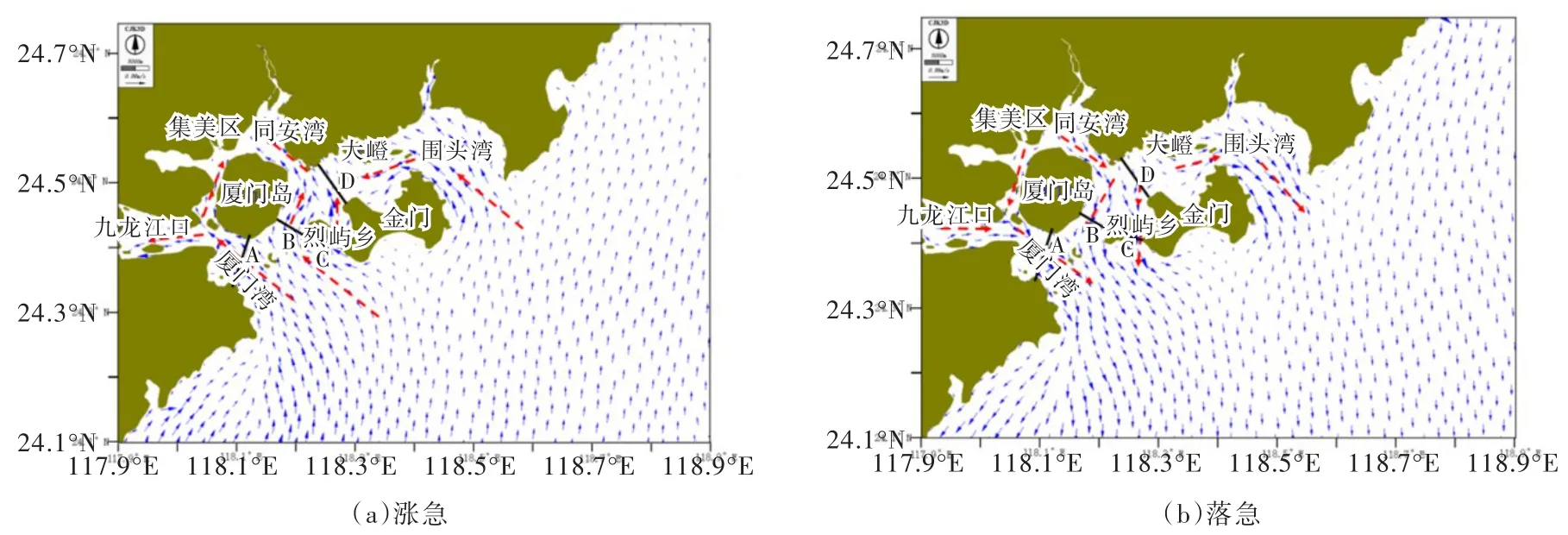
图11 厦门附近海域涨落急流场分布图
表1统计了厦门岛周边的年平均涨落潮流量,断面位置见图10。由表1可知,厦门岛南侧(断面A)与东侧涨潮流量(断面B+C)基本相当,围头湾处的涨潮流量(断面D)相对较小,不足前述断面的三分之一,落潮流量分布趋势与涨潮基本一致,由于金门岛北侧部分落潮流向烈屿乡方向,因此厦门岛东侧落潮流量大于南侧。由此可见,厦门岛周边的潮量主要来自厦门湾口门。

表1 厦门湾各汊道年平均流量统计 (单位:m3/s)
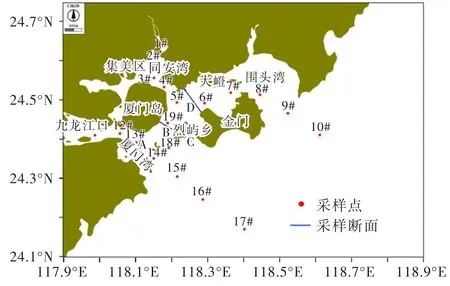
图10 采样点位置图
4.2 汊道潮位特征 图12为厦门附近海域汊道沿程年平均高、低潮位分布特征。潮波自外海向口门内传播,在径流、地形及岸线边界的影响下,高潮位总体呈逐渐升高的趋势,围头湾及九龙江口沿线高潮位变化相对较平缓,同安湾沿线高潮位在厦门岛东侧波动较大,主要因为自厦门湾口门和围头湾口门进入的潮波在厦门岛东北侧(5#点附近)汇合,而金门岛北侧(6#点)高潮位明显高于厦门岛东侧(19#点),因此在水流汇合处(5#点)高潮位升高幅度较大,约为0.11 m,且同安湾高潮位明显高于九龙江口和围头湾。低潮位自外海至口门内,围头湾及九龙江口沿线呈逐渐降低的趋势,潮差逐渐增大;同安湾沿线低潮位变化较为复杂,对于湾内的1#—5#点影响,受径流、地形及围头湾低潮位低的影响,越往湾顶低潮位越高,19#以外各点低潮位受外海低潮位的影响,低潮位升高约0.10 m。由于厦门岛东北侧是厦门湾和围头湾两股潮波传播的交汇点,因此该处高低潮位波动较大,但总体来看交汇处5#采样点的高低潮位与围头湾处的6#点更为接近,与厦门岛东侧的19#点差异较大,因此同安湾的潮波特性与围头湾潮波特性更为相似。
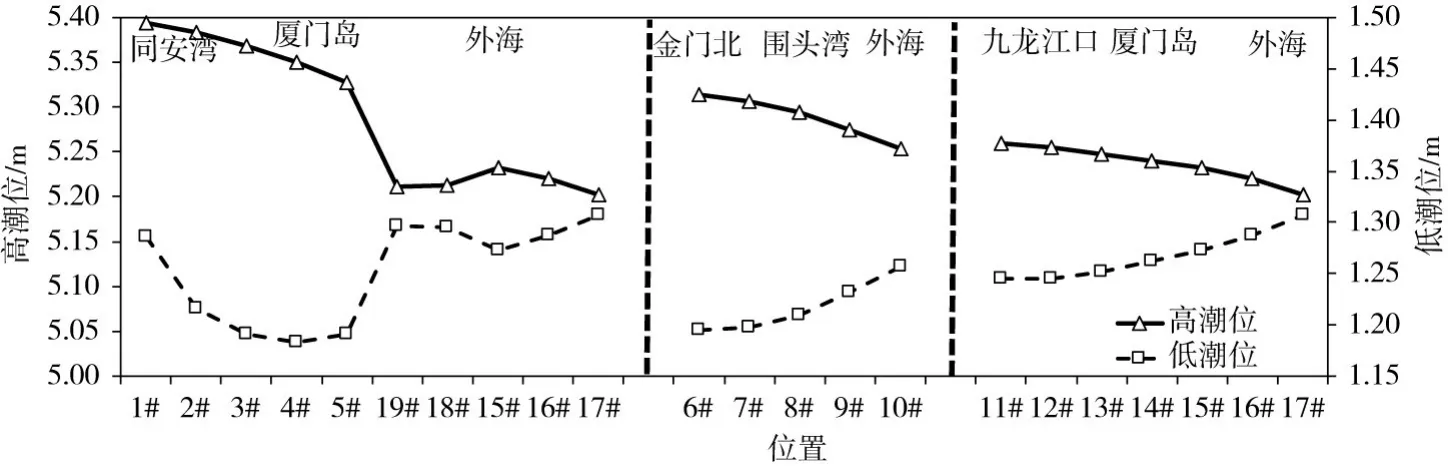
图12 厦门附近海域沿程年平均高、低潮位分布
5 潮汐调和分析
潮波从外海进入河口区后,口门位置和形态的差异导致潮波在传播过程中的变形程度也不同,本节采用具有自主知识产权的CJK-TIDE软件,对数学模型计算结果进行调和分析计算,以此分析潮波在传播过程中的特征和差异,分潮数采用63个分潮。图13为厦门岛附近18#点(位置见图10)部分分潮振幅的分布,由图13知,半日分潮M2分潮占绝对主导地位,其振幅占所有分潮振幅和的41.2%,S2分潮振幅次之,二者占所有分潮振幅和的53.3%,全日分潮K1分潮振幅值最大。图14和图15为厦门附近海域半日分潮M2、全日分潮K1分潮振幅与初相角沿程分布,由图14和图15知,M2分潮自外海向同安湾及九龙江口方向,振幅和初相角总体呈增大趋势,同安湾与外海的振幅比约为1.13,九龙江口与外海的振幅比约为1.24,潮波自围头湾向同安湾方向传播时,至5#、6#点时,振幅降低,这主要因为该处受厦门湾和围头湾两股潮波传播影响,而厦门湾的振幅明显低于围头湾(图14);K1分潮自围头湾向同安湾传播过程中,振幅先增大后减小,在围头湾7#位置达到最大,K1分潮自外海向九龙江口传播过程中,振幅持续增大,由图15可明显看出,九龙江口全日振幅明显大于同安湾。图16为厦门附近海域浅水影响系数沿程分布变化,浅水影响系数一般用HM4/HM2表示,表征潮波变形的程度,由图16知,浅水影响系数自外海向同安湾和九龙江口方向均呈逐渐增大的趋势,说明潮波向岸边传播过程中,潮波变形逐渐加剧,同安湾潮波变形程度大于九龙江口。
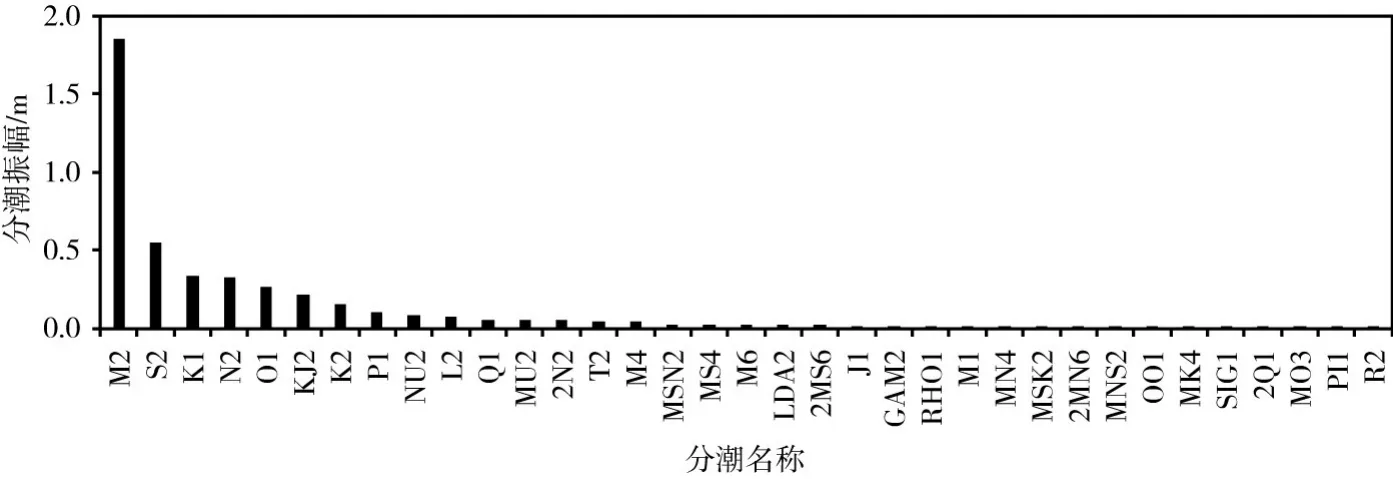
图13 厦门岛附近18#采样点部分分潮振幅分布
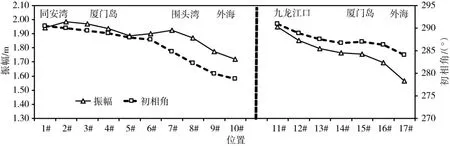
图14 厦门附近海域M2分潮振幅与初相角沿程分布特征
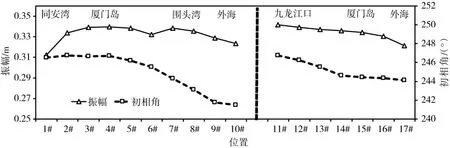
图15 厦门附近海域K1分潮振幅与初相角沿程分布特征
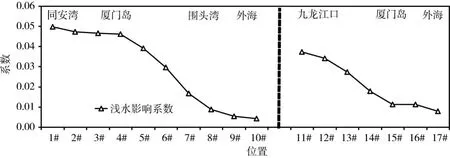
图16 厦门附近海域浅水影响系数沿程分布特征
6 结论
(1)构建了厦门及其附近海域高分辨率二维潮流数学模型,研究了GPU并行计算效率,结果表明GPU并行较CPU单核计算效率可提高约180倍。
(2)厦门岛南侧(断面A)与东侧涨落潮流量(断面B+C)较为接近,围头湾处的涨落潮流量(断面D)相对较小,说明厦门岛附近潮量主要来自厦门湾。潮波自外海向九龙江口、围头湾方向传播,高潮位逐渐升高,低潮位逐渐降低,潮差增大。同安湾方向潮波受厦门湾和围头湾两股潮波影响,其潮波特性与围头湾更为相似。
(3)潮汐调和分析结果表明,厦门海域M2分潮占绝对主导地位,其振幅占所有分潮的41.2%,S2分潮振幅次之,二者占所有分潮振幅和的53.3%,全日分潮K1分潮振幅值最大。同安湾与九龙江口M2分潮振幅接近,K1分潮九龙江口振幅较大,潮波变形程度同安湾较大。
