T型圆钢管相贯节点超低周疲劳断裂及极限承载力分析

2021-09-09孟文清张翰阳

结构工程师 2021年2期

孟文清张翰阳尹越

（1.河北工程大学土木工程学院，邯郸 056038；2.天津大学建筑工程学院，天津 300072）

0 引言

钢结构焊接节点在地震荷载作用下极易发生断裂进而导致事故的发生，它们通常以大应变和超低循环为特征，当应变远大于屈服应变，在载荷循环数在几十周以内时，就会发生断裂破坏，属于韧性断裂。而当前对于断裂的研究主要采纳传统断裂力学方法，断裂力学的应用前提是假设裂纹已经存在，初始裂纹尖端处有着高应变约束。因此，它主要适用于屈服强度非常有限的脆性断裂研究，而不适合于在低周反复载荷下无宏观初始缺陷且出现明显屈服现象的韧性断裂，因此传统断裂力学方法不适用预测地震引起的结构断裂。而基于微观机制的断裂模型可以掌握应力应变场对断裂预测的影响，在出现大面积屈服区域且区域无初始裂纹的情况下，可以准确地预测韧性裂纹的发展，从而可以用于预测地震造成的断裂［1］。然而，现阶段关于微观力学模型应用的研究还是多处于材料的量级上，而把其宏观应用于预测地震荷载作用下钢结构焊接节点断裂的力学性能上的研究还较少。

相贯节点是现在众多钢管连接方式中应用最为广泛的一种，相贯节点的破坏极大可能会引起被连接杆件的失效，从而引起整体结构的破坏，因此节点是否被破坏是作为连接各个杆件交汇的关键所在。近几年来相贯节点的研究主要集中在静荷载下承载性能方面，并逐渐趋于成熟［2-5］，而现阶段对动荷载下抗震性能与疲劳机理这一领域的研究更为急需，用以填充低周反复荷载作用下的弹塑性滞回性能这一空白领域。

本文对往复荷载作用下圆钢管直接焊接节点试验进行模拟，使用校准后的基于微观断裂机制的CVGM模型来预测节点的断裂，并将预测结果与实验结果进行比较，以验证在往复荷载作用下微观断裂模型对于预测钢结构相贯节点韧性断裂的适用性。在此基础上利用ABAQUS子程序VUSDFLD结合微观断裂理论的裂纹扩展模型对节点进行模拟，验证裂纹扩展对节点承载力的影响。

1 微观断裂模型

1.1 基于微观断裂机制的循环空穴扩张模型

Kanvinde和Deierlein［6］指出对于循环加载下需要考虑加载过程中三轴应力的正负变化，当三轴应力为正时，空穴扩张，为负时则收缩。而等效塑性应变却是不断累加的，因此对应力三轴度取绝对值，在循环荷载作用下有：

式中：c为常数，空穴尺寸变化比率；R为瞬时空穴半径；T为应力三轴度；dεp为等效塑性应变增量。

已知受拉和受压过程中空穴尺寸变化比率不变，当处于临界空穴扩张比时，取c1=c2=c，将式（1）按受拉和受压进行分解，c值移至等式左侧进行简化得到如下式：

式中，ηcyclic是循环荷载作用下材料的韧性参数，其在单调荷载下的韧性参数ηmonotonic的基础上考虑一损伤函数：

式中，λCVGM是循环荷载作用下材料的损伤参数，可由圆周平滑槽口试件在往复荷载作用下试验进行校正和取值。

最终CVGM模型的计算公式为

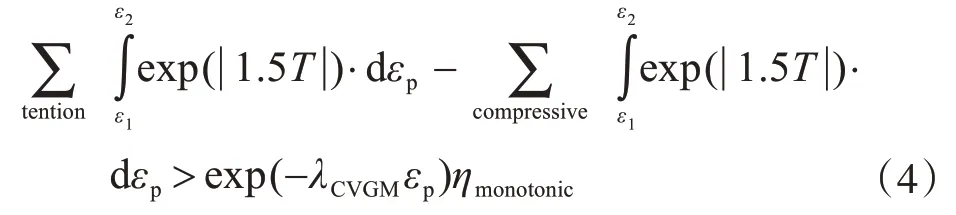
当式（4）得到满足时，CVGM判据即认为该材料点已满足超低周往复荷载下发生韧性断裂的临界状态，即该点已发生开裂。上述对材料断裂的判定中都是针对某种荷载下材料某点的断裂失效，属于微观的一种，但在实际中，裂纹出现是宏观现象。所以需要将断裂的定义由微观不可见转为宏观可见，因此引入了材料的特征长度l*。给与特征长度l*一个定义：特征长度是保持材料力学性能的最小长度，即从微观角度来说是长度内所有材料点的集合，当集合内的材料点根据微观断裂判据均达到断裂的临界条件，即认为发生了延性断裂，宏观裂纹出现。

Kanvinde［7］提出了两个界限值和一个最可能值的微观断裂判据中特征长度的确定方法，l*的大小取决于材料本身的微观结构，可以通过对材料断口电镜扫描得到。其中，特征长度的界限值上限是电镜扫描得到的相邻两个最大凸起或相邻两个凹陷部分之间的距离，而界限值的下限为平均波纹直径的两倍，最可能值是连续10个凸起或连续10个凹陷直径的平均值。常用的结构钢材特征长度一般在0.1～0.4 mm范围内。

1.2 基于微观断裂机制的裂纹扩展理论

根据断裂力学的理论，裂纹达到临界长度的时刻即为断裂发生时刻。因此在这里引入裂缝拓展速率与塑性应变幅之间的关系［8-9］，如式（5）所示：

式中：α为裂纹长度；Δεp为塑性应变幅；N为循环的圈数；α，β为材料本身属性参数。

为了更合理地考虑应力三轴度对裂纹扩展的影响，在结合Kanvinde和Deierlein［6］韧性断裂理论的基础上，重新定义延性应变幅的表达式如下：

对于荷载作用下变形较小的材料，应力三轴度在塑性增长过程中通常保持稳定，在此假设应力三轴度在单次加载过程中保持不变，则其延性应变ε*p可以简化为以下表达式：

在此，利用雨流计数法，即可统计得到每个循环的有效塑性应变幅，因此式（9）可简化为

其中，式（12）中系数αexp(β1.5T)的计算方法如下：

式中，ai和ai+1分别为第i次和i+1次循环时的裂纹长度，在单次加载中我们认为在一个拉伸或压缩过程中应力三轴度基本保持不变，因此公式中用到过的应力三轴度为第i次循环过程中的平均值。

当式（13）计算得到的裂缝长度ai+1大于临界裂缝长度af时，即认为断裂发生。

2 断裂扩展的数值模拟

有限元原理来源于连续介质力学，假定物质可以划分为多个微观结构的集合，集合中每个微观结构的变化都会引起相邻微观结构的变化，之后定义边界条件进行计算。而微观结构在有限元中表现出来的就是网格单元，因此网格单元不可以轻易删除。当需要通过有限元模拟工程中切削、断裂、破坏的情况时，可以利用ABAQUS［14］单元失效的功能来进行模拟。用户可通过FORTRAN或Python进行编程，子程序方法最为灵活，难度也最大。需要在VUSDFLD子程序中定义一个状态变量来表征材料是否失效。在每一次更新结果后都会对状态变量进行判定，当变量输出为0时，表示失效，不再参与下一步计算；变量输出为1时，则表示正常。然后根据自己在子程序中定义的失效准则和本构方程来给这个状态变量赋值。上述方法中的失效单元在模型中体现为单元删除，不会被重新激活。

基于CVGM断裂判据进行韧性断裂扩展分析时，为了保证计算精度，需要将有限元网格细化到材料的特征长度，这将造成单元数量过多、计算代价过大的问题。可以采用一种基于CVGM的断裂扩展模型［10］，通过校对较大网格与小网格断裂时刻的函数关系，以采用较粗网格的有限元模型准确模拟韧性断裂的扩展［11］，理论参照1.2节。在有限元计算过程中，状态变量每次更新都将满足CVGM断裂判据的单元从模型中删除，用来模拟裂纹开裂后的裂纹扩展过程，模拟节点的抗震承载力性能的变化。

3 节点超低周疲劳断裂预测

3.1 试验概况

本文采用模拟的试验来源为邵永波等［12-13］对4组T型相贯节点进行的拟静力滞回性能研究，由于本文主要研究内容为对直接焊接节点在超低周往复荷载下的韧性断裂的预测以及断裂对节点抗震性能的影响，因此选用试验中两组不同尺寸、不同加载幅值的非加强型节点进行研究，试验所用钢材均为Q345B，几何参数如图1和表1所示。

图1 节点形式示意图Fig.1 Joint form diagram

表1 节点尺寸表Table 1 Joint size table

T型节点的加载是通过支管端部与电液伺服动静万能试验机连接施加竖向往复循环荷载。主管端部通过螺栓与试验台上支座铰接，从而实现理想的边界约束条件，在主管下方正中放置位移计，如图2所示。支管加载端施加的荷载以及加载端的竖向位移值可以通过与试验机相连的电脑程序中得到。

图2 实验装置图Fig.2 Experimental setup

试验机有荷载控制与位移控制两种加载方式。在弹性阶段可以采用荷载控制与位移控制两种方式。因此参照《建筑抗震试验规程》（JGJ 101—2015）［15］要求，采用荷载-位移双控制的加载方案，将加载过程分为两个阶段，在节点屈服前的弹性阶段使用荷载控制，分别以50 kN、100 kN为每级荷载，每级荷载循环一次，JD-1以先施加轴向拉力再施加轴向压力为一循环，JD-2以先施加轴向压力再施加轴向拉力为一循环。荷载控制循环两圈后换为位移控制，位移控制以屈服点位移Δy=10 mm为参考位移，每级加载时增大1/2Δy，即5 mm，每级加载循环1次，加载速率取10 mm/min，逐级加载至节点破坏，彻底失去承载力。

3.2 有限元模型的建立

采用大型通用有限元分析软件ABAQUS对T型圆钢管相贯节点进行建模和分析。节点模型参照规范［16］建立模型为考虑相贯线实体焊缝的有限元模型［17］。因为节点只加载轴向荷载，因此利用关于主支管轴所在平面对称的半模型进行计算，节约计算成本，减少计算时间；单元尺寸确定要求有两点，第一是要保证节点计算的精度，这就体现在节点区域网格越密集越精确，同时还要考虑节点网格加密区与非加密网格过渡问题，尺寸相差过大会导致计算不收敛等问题；第二要保证网格数量尽量少，网格数量过多，变量太多，计算时间过长。经过试算，当节点域单元尺寸不大于2 mm，非加密区单元尺寸6 mm时模型收敛，计算结果较好，模型整体采用八节点线性减缩积分C3D8R单元；如图3所示，主管和支管的长度按照试验建模，主管两端铰接，在对称面设置对称约束条件；加载方式采用在支管端部表面耦合点上沿z轴施加轴向荷载施行，加载制度如图4所示。

图3 整体模型和焊缝区域示意图Fig.3 Overall model diagram and schematic diagram of weld area

图4 JD-1和JD-2加载制度示意图Fig.4 JD-1 and JD-2 Loading system diagram

3.3 有限元分析

通过对整体模型的初步分析，如图5和图6所示，可以得到节点在往复荷载下的等效塑性应变云图和应力云图。在Pressure应力云图中，区域受拉时，Pressure应力数值为负，而有效塑性应变则是单调累加的，因此在PEEQ最大的区域代表着塑性应变累加最快的区域，当两者重叠的区域就是最容易发生韧性断裂的位置。因此，节点的断裂位置推测为受拉支管与主管相交的焊趾处。为了利用微观断裂的方法准确地预测断裂发生的位置和时间，需要用与钢材材料特征长度l*接近的网格尺寸，从材料的尺度来模拟断裂的发生，为了减少计算成本，在此处采用子模型技术进行更为细致的断裂预测分析，子模型网格尺寸网格尺寸取为0.3 mm［18］，如图7所示。子模型同样采用八节点线性减缩积分单元C3D8R。

图5 JD-1和应变PEEQ云图Fig.5 JD-1 and JD-2 Distribution of PEEQ

图6 JD-1和JD-2 Pressure应力云图Fig.6 JD-1 and JD-2 Pressure distribution

图7 子模型示意图Fig.7 Sub-model diagram

有限元模型采用Q345钢材，断裂判据中材料韧性参数η和λ的取值参考廖芳芳、王伟等［18-19］对Q345钢材热影响区通过多组试件校对出的韧性参数η和λ，即η=2.53，λ=0.33。他们在文中对在断裂预测中关于韧性参数的敏感性进行了分析，证明韧性参数η和λ放大或缩小20%，断裂预测结果近似相同，可以用于标号相同钢材；图8是节点的子模型计算后的等效塑性应变云图，对其中单元上数据进行提取，根据计算的空穴扩张指标VGI达到临界空穴扩张指标时，则代表断裂发生，可以进一步预测断裂发生的时间以及断裂位移，如图9所示。

图8 子模型等效塑性应变云图Fig.8 Sub-model PEEQ cloud

图9 基于CVGM判据断裂预测Fig.9 break prediction based on CVGM criterion

根据试验结果显示，JD-1与JD-2最终破坏都发生于滞回加载的第9圈，而有限元预测JD-1断裂发生在滞回加载的第7圈，JD-2断裂发生在滞回加载的第8圈，有限元计算结果与试验结果相差不大，CVGM模型可以较为准确地预测节点的断裂时刻。

3.4 韧性断裂扩展的数值模拟

在节点承受往复荷载时裂纹往往较早地出现，节点在破坏前通常是带裂缝工作，通过塑性变形及裂缝的扩展共同来消耗能量，此时承载力并不会突然降低，因此不能用裂纹发生时刻来表示节点的极限状态，需要考虑节点在往复荷载作用下裂纹的扩展行为，来更合理评估节点的极限状态。因此本节中拟采用基于微观断裂机制的裂纹扩展模型，对节点在往复荷载下裂纹扩展过程中承载力性能变化进行分析。

有限元模型采用上节中建立的模型，求解器选用动态求解器。为了避免隐式分析容易出现的不收敛现象，设定时采用显示动力计算方法进行计算，当分析步时间足够长时，不会出现因动力效应而造成的不平滑加载现象，计算精度也可以达到隐式分析步达到的计算精度。ABAQUS在计算时自动读取编写的VUSDFLD子程序，当单元满足式（13）时，即认为单元内部已经形成贯通裂缝，则将该单元删去，以模拟裂纹扩展的过程，参考车鑫宇［20］在论文中对参数的取值，如表2所示。

表2 裂纹扩展模型参数取值Table 2 Parameter value of crack growth model

在图10（a）中给出了JD-1试验和有限元分析结果的对比情况，有限元模拟的滞回曲线与试验得到的滞回曲线吻合较好，在4.2节中，通过子模型方法判定裂缝启裂出现在节点的第7圈的受拉阶段，从图中可以看出，此时节点的承载力未发生突变。随着位移幅值的加大，应力三轴度指数倍上升，单元损伤不断累积，导致单元在满足判据后不断被删除，具体表现为焊趾热影响区裂纹不断扩展，断裂区域逐渐变大。随着裂纹的不断扩展，节点承载能力随着趋势平滑下降，在第8圈的受拉阶段节点的承载力曲线在峰值处出现明显的下降，紧接着在第9圈垂直支管与主管相交处焊缝的撕裂节点破坏；图10（b）中给出了JD-2试验和有限元分析结果的对比结果，与JD-1类似节点性能变化类似，节点在第8圈的受拉阶段发生开裂，在第9圈的受拉阶段节点承载力明显下降，直到在第10圈受拉时裂缝完全裂通，节点破坏。JD-2晚于JD-1破坏的原因可能为JD-2承载性能本身优于JD-1，并且支管尺寸大，焊缝与主管角度较大，损伤不易累积。另外，有限元结果与试验结果在拐点处存在偏差，主要是有两方面原因：一方面是显示动态分析中不易控制分析步时间，加载时长大于或小于所需时长，导致模型实际加载位移会与设置的位移产生差别；另一方面，在受压阶段，断裂后模型的支管开裂面在向下移动时与主管断裂面重新接触，因此承载力与试验所得数值有所区别。