砂泥岩混合填料湿化变形与沉降计算方法

2021-09-09云海浪韩文喜张日华胡伦俊

科学技术与工程 2021年22期

云海浪，韩文喜，王波，张日华，胡伦俊

(1.成都理工大学环境与土木工程学院，成都 610059； 2.成都理工大学地质灾害防治与地质环境保护国家重点实验室，成都 610059； 3.河北建设勘察研究院有限公司，石家庄 050000； 4.中国建筑西南勘察设计院有限公司，成都 610000)

西南地区砂泥岩填料作为混合填筑材料，由于雨水的侵入作用使得该填筑体强度降低，经常发生湿化变形，对工程存在巨大安全隐患。目前，很多学者对软岩和堆石料湿化变形特性进行研究。其中，刘辉[1]采用双线法对变质软岩轴向湿化变形和湿化体变规律展开分析，并通过拟合提出湿化变形经验公式；殷坤垚等[2]对风干和饱和状态软岩填料进行试验，通过分析围压对湿化变形规律的影响，得出湿化变形发展分为两个阶段；李青山等[3]对巴东组土料进行不同压实度、不同围压的湿化变形试验，得出湿化变形随湿化点偏应力增大而增大，附加轴向应变随围压增大而减小；丁艳辉等[4]对土石坝堆石料展开快速湿化三轴试验，主要研究堆石料湿化变形的过程、特性及发生机制。随着湿化变形在机场地基处理中成为重点，部分学者对砂泥岩类填料的湿化变形机制进行研究。王胜杰[5]阐明填筑体在湿化条件下的沉降机理并提出避免措施；付泓锐[6]通过砂泥岩三轴剪切试验，探究周期性饱水作用对饱和砂泥岩混合料抗剪特性的影响；杨洋[7]提出了周期性饱水砂泥岩混合料的压缩试验方法，得出砂泥岩混合料的压缩流变计算方法。

由于湿化变形对填筑体的变形、稳定带来巨大困扰，学者在湿化变形机理的基础上对变形量以及变形量计算方法展开研究。赵振梁等[8]对斜心墙堆石坝砂岩粗粒料采用单线法进行中型三轴湿化变形特性试验，提出湿化变形数学模型。周雄雄等[9]采用单线法对粗粒料进行试验，提出湿化体变与湿化轴变比值的计算方法和湿化轴变与湿化应力水平的双曲线关系。杨培浩等[10]将湿化轴向应变分为由围压引起的应变和由偏应力引起的应变两部分，分析其规律提出湿化变形计算公式。介玉新等[11]认为在某一应力状态下的湿化变形是由两部分，由材料本身刚度引起的湿化变形可用双线法确定，由湿化引起的附加变形可通过单线法结合双线法确定。

为研究西南地区砂泥岩湿化变形规律以及湿化后沉降变形，以成都天府国际机场砂泥岩填料为研究对象，使用GDS三轴试验仪对直径为300 mm、高度为600 mm的试样展开湿化变形研究。通过室内试验得出砂泥岩湿化变形计算方法，结合分层总和法进行沉降变形计算，并通过数值模拟进行验证。

1 砂泥岩混合料湿化变形试验

1.1 试验材料

本次试验所用土料取自成都天府国际机场T2航站楼南侧附近，均为砂泥岩填料。颜色呈紫红、砖红，砂泥结构互层，节理发育明显。根据现场试验得出砂泥岩最优配比为7∶3，现场砂泥岩填料的天然含水率为2.68%。最优含水率为10.1%，最大干密度为2.01 g/cm3，现场级配曲线如图1所示。

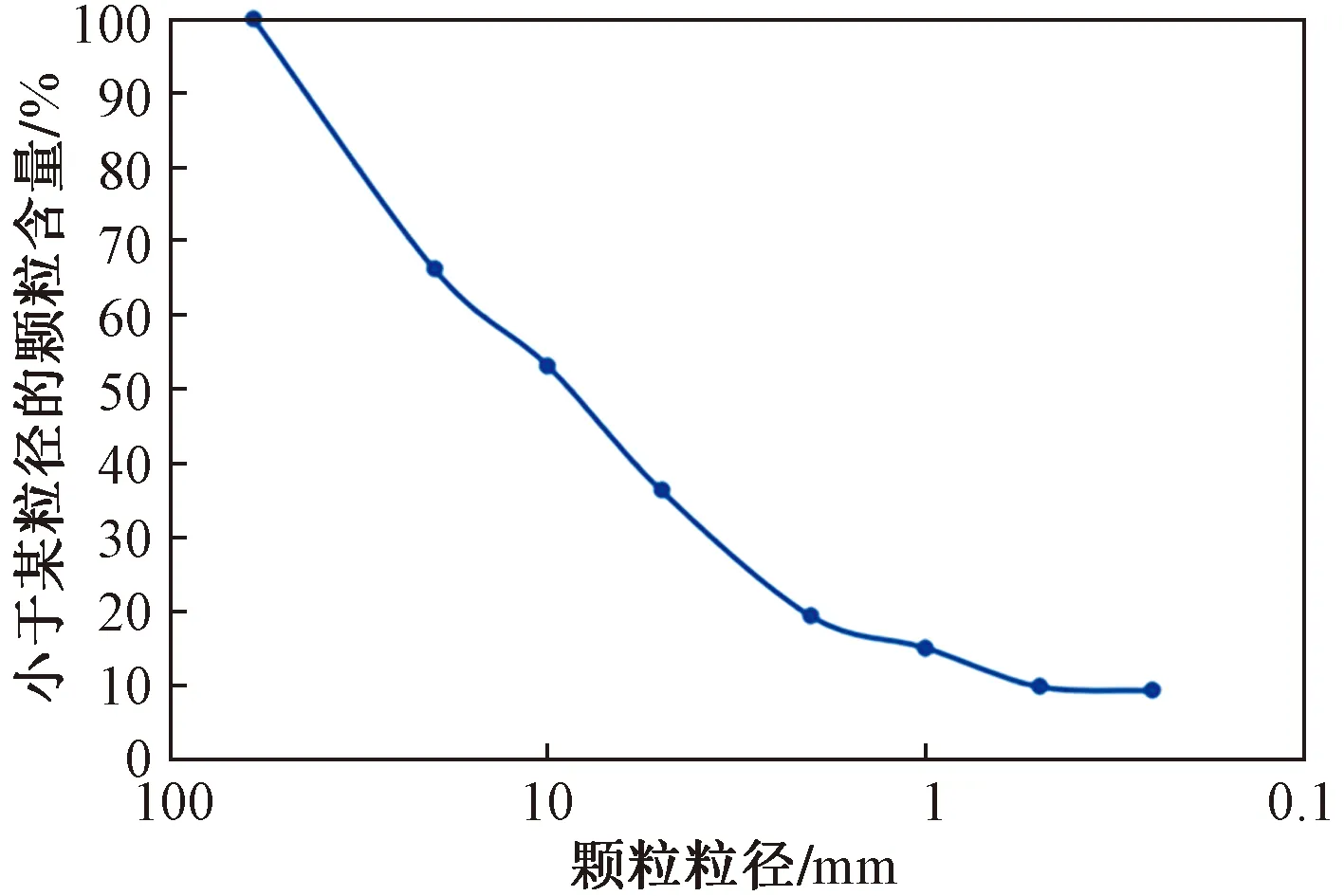
图1 级配曲线图

1.2 试验方案

试验所用砂泥岩混合料的相应级配、含水率与现场填料保持一致。试样均为直径300 mm、高度600 mm，最大粒径为60 mm。本次湿化变形饱和样采用饱和水头法[12]进行饱和，注水水压为350 kPa，水流从试样底部注入，从试样顶部出水口流出，直至流入水量与溢出水量相等为止。结合相关文献[1-2，13-14]设计试验方案如表1所示(未设置平行试验)。

表1 试验方案

1.3 试验仪器与试验步骤

本次试验使用最新引进英国的GDS三轴试验仪，试验装置主要由压力室、轴向加压设备、围压施加系统、体积和孔隙压力量测系统和计算机控制与分析系统几部分组成，如图2所示。该套系统吸取了先进的机械制造工艺和自动控制技术，量测、控制精度高且实现了数字化操作。试验主要步骤如下。

图2 GDS三轴仪

(1)填料加工：在实验室经过风干、碾碎、过筛，根据现场填料所使用的砂泥岩配比和级配制作砂泥岩颗粒试样原料，配置所需含水率。

(2)试样制备：制作直径为300 mm，高度为 600 mm 的试样，如图3所示。根据试样密度计算，分别称取各级粒径下填料质量，并配置相应含水率进行充分搅拌。试样分6层击实，每层装入等量土料，使用击实锤对每层击实，达到每层要求高度 10 cm 时，对表面进行抛毛处理，减少人为因素降低试样强度。

图3 试样制备

(3)装样：将压力室放到加载架上，使加载中心与试样中心、压力室活塞杆中心在中轴线上，安装位移传感器、孔压传感器，关闭孔压控制器阀门、压力室排水孔。

(4)试验设置及运行：将位移传感器归零，围压调至300 kPa，根据试样要求应力水平为0.25、0.5、0.75的轴向偏应力值。

(5)终止试验：该试验全过程以应变速率为 0.1 mm/min 施加轴向偏应力，直至轴向应变达15%视为完成试验[15]，破坏后试样如图4所示。

图4 剪切破坏后试样

2 结果分析

2.1 湿化应力应变曲线

整理试验结果作干样和湿样的应力应变曲线图，如图5所示，轴向应变以压缩为负，围压为300 kPa。

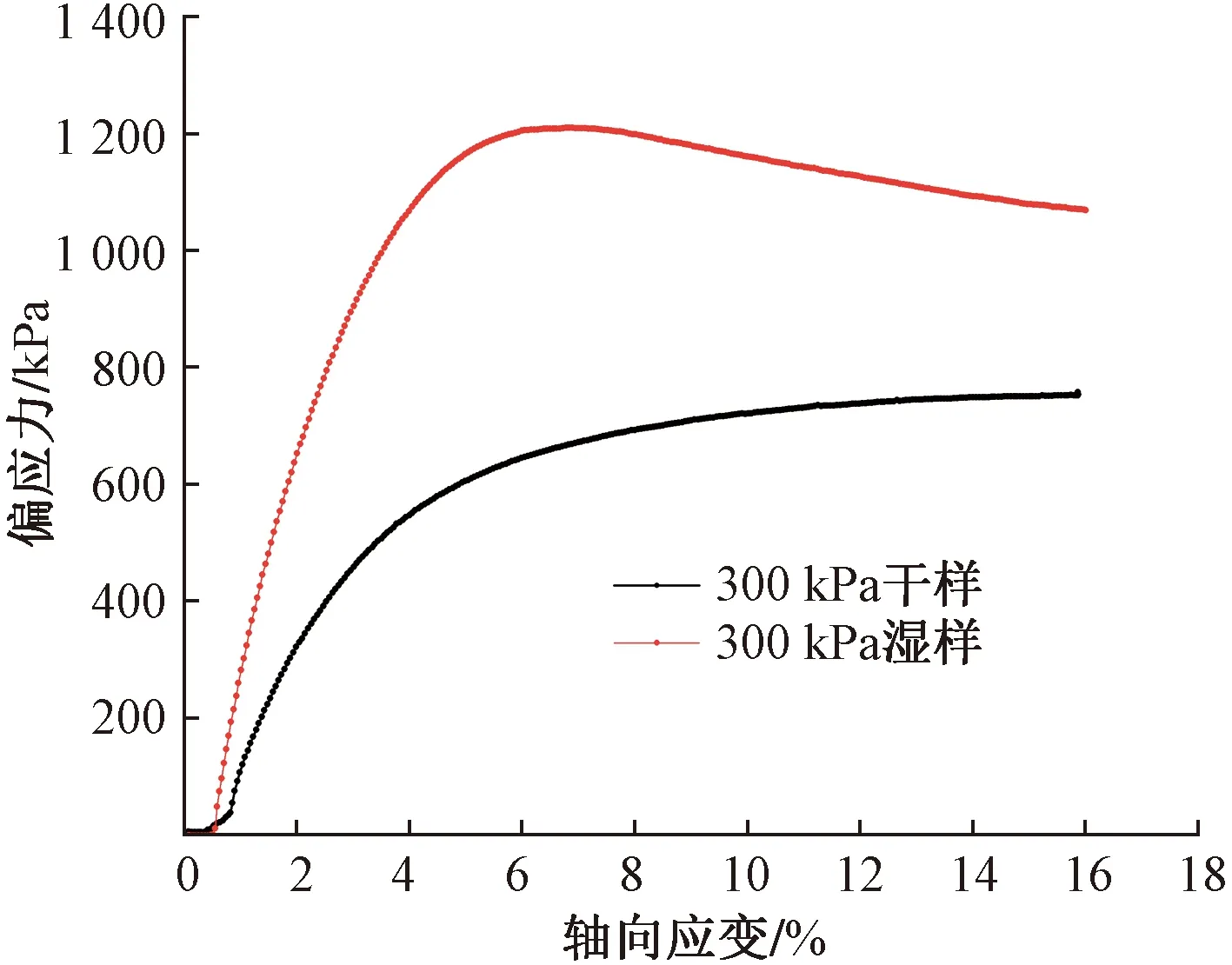
图5 干样与饱和样应力应变曲线图

由图5可知，干样在300 kPa围压下峰值偏应力为1 200 kPa，根据此数据可确定湿化试验所施加的应力，为最大偏应力的0.25、0.5、0.75。在饱和样剪切试验中，施加约50 kPa的周围压力，水流从试样底部注入，从试样顶部出水口流出，直至流入水量与溢出水量相等，认为其达到饱和要求，然后在300 kPa进行固结剪切破坏。分析图中应力应变曲线可得出的结论如下。

(1)干样的最大破坏偏应力为1 200 kPa，而饱和样的最大破坏偏应力为750 kPa，干样湿化后，其强度下降了约1/3。

(2)砂泥岩干样的应力应变曲线呈软化型；饱和试样的应力应变曲线一直位于干样的下方，呈现出S型。结合姜景山等[15-16]、左永振等[17]利用CT手段研究湿化变形，分析其原因可能是由于水的侵入，软化和润滑了粗粒土颗粒，颗粒间产生滑动、破碎，颗粒位置发生重新调整，导致土颗粒的强度降低，削弱了应变硬化。因此随着应变的继续增长，应力渐渐趋向于一条直线。

2.2 湿化应力水平对湿化变形的影响

砂泥岩混合料在0.25、0.5、0.75的应力水平下浸水的变形时间曲线如图6所示。

从图6可以看出，在施加相应的应力水平的前2 000 s(33 min)内，试样迅速产生变形，该阶段变形快是因为施加荷载，且施加的荷载越大，变形越大。(在干样的三轴剪切试验中已确定干样在300 kPa围压下的峰值破坏应力为1 200 kPa，因此试样在相应应力水平下不会发生破坏。)

图6 砂泥岩填料在不同应力水平下的变形时间曲线

保持试样围压、应力水平不变，监测记录位移数据，发现试样在经过5 000 s(80 min)左右后，位移数据基本不会发生变化。待位移数据稳定后开始向试样注水，可以发现趋于稳定的试样开始继续发生变形，经过7 h的浸水湿化变形后重新稳定，此时可以看出试样的出水孔在均匀、稳定的出水，可以认为试样的湿化已经完成。砂泥岩填料干样、湿样与湿样分别在0.25、0.75应力水平下的应力应变曲线如图7所示，试验可得出以下结果。

图7 0.25、0.75应力水平下湿样与干样、湿样的应力应变曲线

(1)砂泥岩填料在三轴压缩试验中的应力应变行为最初遵循干样的应力应变曲线，在经受浸水湿化后遵循湿样的应力应变曲线。

(2)砂泥岩填料在0.25、0.75应力水平下，其直线部分为湿化变形期间，在此期间，水在不断地注入试样湿化，可以发现应力水平越大，其湿化变形量越大。当应力水平下湿样开始湿化时，其偏应力会发生骤降，分析原因可能是水的注入致使试样内部孔隙水压力升高，使轴向压力骤降；偏压力的下降幅度与围压、应力水平有关，围压越大、应力水平越高，其偏应力下降幅度越大。

试样在注水后发生的变形直至稳定，在此期间发生的变形量认为是湿化变形，砂泥岩填料在不同应力水平下的湿化变形如图8所示。

从图8可以发现，砂泥岩填料在注水初期的变形增长相对较快，用不到20%的变形时间发生整体80%的变形量，而后变形放缓慢慢趋于稳定。另一方面，在同一围压下，湿化变形量随着湿化应力水平的增大而增大，在应力水平较大时，湿化变形增加的幅度也比较大。一些学者分析其中原因，应力水平越高时，试样在注水条件下的颗粒间的接触、错动、滑移越大，内部应力越大，造成的颗粒破碎、颗粒软化越剧烈[18-19]。此外泥岩土性较软，强度比砂岩强度差，在较大应力水平下会更容易破坏。

图8 砂泥岩填料在不同应力水平下的湿化变形

为了探究湿化应力水平对湿化变形的影响，将砂泥岩填料在不同应力水平下的湿化变形统计出来，不同应力水平下湿化变形如表2所示。

表2 不同应力水平下湿化应变

分别采用指数型、线性、对数型、乘幂型关系对湿化变形和应力水平拟合，其拟合效果如表3所示。

表3 不同拟合类型下拟合效果表

从表3可以看出，湿化变形量与湿化应力水平用指数形式拟合效果最好，表达式如式(1)所示：

εw=aebs

(1)

式(1)中：εw为湿化变形量，mm；a、b为与材料、围压有关的参数；s为应力水平；e为自然常数。

可以得出，湿化变形量与湿化应力水平从经验法上讲是符合指数型关系的。可以根据相关试验得到a、b值，算出单次湿化变形量。

3 考虑湿化变形的回填区域沉降变形分析

3.1 考虑湿化变形的沉降变形机理

通过对成都天府国际机场飞行区大铁(东区)表层、地面、水位、孔隙的监测点分析，回填区域的沉降变形可分为原地面沉降变形、填筑体沉降变形、湿化变形。沉降变形受到上覆荷载、土体性质、地下水位等条件的影响。具体可分为以下4部分。

(1)瞬间变形：在土体受荷初期发生，土体受到荷载发生剪切变形形成的沉降，变形所用时间短、速率快，堆载高度和软土厚度对其影响很大。

(2)主固结变形：随后由土体内部孔隙水压力的消散引起的沉降变形，占总沉降变形的大部分。

(3)湿化变形：因为降雨或者其他因素导致的地下水位升降，由于水的浸入湿化作用[18-19]，使土颗粒软化并润滑，使原先稳定的颗粒接触状态变得不稳定，颗粒位置重新调整，接触得更为紧密，导致变形增大，但软化和润滑所导致的强度降低要大于挤密作用所带来的强度提高，最终使粗粒土在湿化后强度降低。

(4)次固结变形：在填筑结束后较长一段时间内，填筑体相当于固定荷载，由于土中超孔隙水压力基本消散完成，在有效应力不变，土体颗粒之间仍发生缓慢移动造成土体的微量变形沉降。

3.2 考虑湿化变形的分层总和法计算

分层总和法假定土体为各向同性弹性体，以弹性力学的应力应变为基础来计算，忽略了土体的塑性变形，因此算出的沉降变形比实际地基沉降变形要小。在实际工程中，土体受到三个不同方向的应力，地基沉降变形包括竖向沉降变形和侧向变形两种。计算土体深度越深，侧向变形越大，因此性需要乘以修正系数来矫正计算的总沉降量。但尽管如此，因为实际工程地质条件的复杂性，考虑到地下水位回升对影响范围内土体产生的影响，提出考虑湿化变形的分层总和法计算沉降变形。在分层总和法的基础上加上由式(1)提出的湿化变形计算方法，即

S=S1+S2

(2)

(3)

S2=aLebs

(4)

式中：S为沉降变形，mm；S1为分层总和沉降变形，mm；S2为湿化变形，mm;e1i为根据第i层的自重应力平均值从e-p曲线上得到相应的孔隙比；e2i为根据第i层的自重应力平均值与附加应力平均值之和从e-p曲线上得到相应的孔隙比；Hi为第i分层土的厚度；s为应力水平；a、b为与材料、围压有关的参数；L为地下水位影响砂泥岩填料深度(通过现场监测得到)。

选取由于地下水位上升产生变形的表层点BC792，其附近钻孔XK3024上覆有14 m厚的砂泥岩填料。根据分层总和法算出在天然状态下的沉降变形量S1，如表4所示。

表4 分层总和法计算表

湿化变形沉降量S2=aLebs，由2.2节可知a=0.004 8、b=3.006，根据监测可知在2019年5—7月的地下水位进入填筑体高度为2 m，因此L=2，得到S2=17.5 mm。总沉降变形量S=S1+S2=121.22 mm，与实测BC792的沉降量相差4.52 mm，根据经验其误差在允许误差范围内。

通过地下水进入填筑体高度和式(2)考虑湿化变形的分层总和计算方法得到飞行区(东区)沉降变形如表5所示。

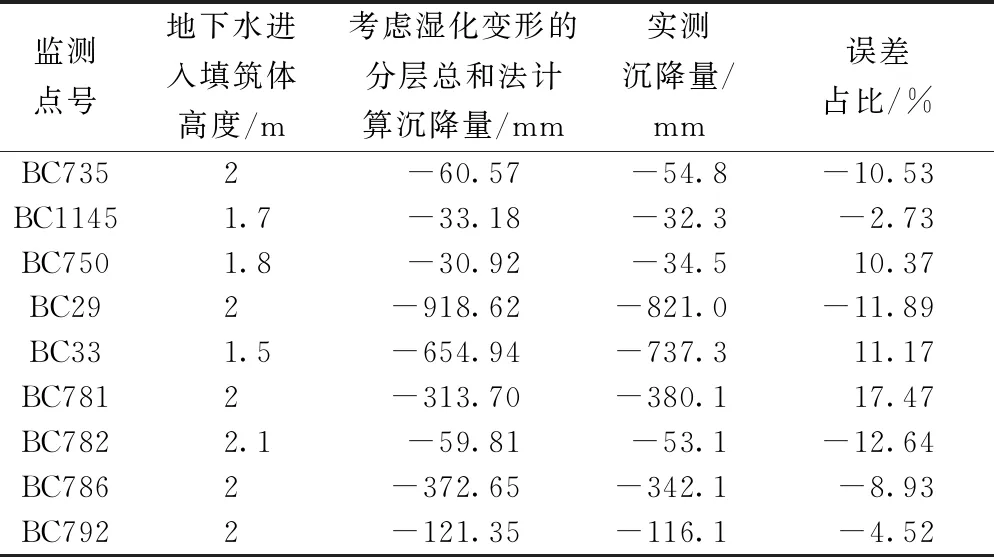
表5 飞行区(东区)沉降变形表

从表5中可以看出，考虑湿化变形的分层总和法的差值占比为-12.64%～17.47%。证明了考虑湿化变形的分层总和法的半经验的数学公式针对成都天府国际机场沉降变形计算是相对准确的，可以用来计算回填区域的湿化变形。

4 考虑湿化变形的回填区域沉降变形数值模拟

PLAXIS数值模拟法可以设置施工工序，通过监测水位数据可以将地下水位变化趋势体现出来。其本构模型中双曲线模型可根据土体湿化前后力学性质改变，通过地下水位线的变化来确定发生湿化变形的土体范围，根据力学性质的改变来计算其湿化变形。因此选择PLAXIS数值模拟法进行砂泥岩填料湿化变形的模拟。PLAXIS的不足在于双曲线模型存在8个特征参数，参数的选取对于性质的敏感性尚未探讨。

4.1 本构模型选择

通过对PLAXIS中本构模型的梳理，针对飞行区大铁(东区)中砂泥岩填料、可塑性黏土和砂质泥岩的沉降变形和湿化变形计算选用Hardening-Soil模型，其优点在于该模型可以很好地模拟土体因应力状态的变化其力学性质变化的情况，并可以模拟实际工程中地下水位回升对土的应力状态造成的改变。

4.2 土体参数确定

通过现场试验、室内三轴湿化试验确定土体参数，在分步施工工序中设置变化的地下水位来模拟地下水位在工程实际发生的变化，模拟考虑湿化变形的填筑体的沉降变形。即可根据本构模型的特征参数来确定模型土体材料参数。

(1)m：刚度依据某个幂率的应力相关性；在软土这种特殊情况下，使用m=1是现实的。

(5)c、ψ、φ：依据Mohr-Coulomb 模型的破坏模式确定。

模型土体等材料参数来源于《成都新机场详勘总报告》《货运区地区检测报告》《成都天府国际机场飞行区工程全场地基处理工程施工图设计说明》以及室内三轴湿化试验，具体参数如表6所示。

表6 模型土体参数

4.3 数值计算结果与分析

确定模型土体参数后，将建好的数值模型生成网格，根据监测资料设置模型初始水位和荷载，初始工序设置完成后，开始进行数值计算。首先设置分步施工工序，根据水位监测点水位变化及对应时间确定时间间隔和地下水位线，时间间隔-水位变化如表7所示。

根据表7设置了8次工序，详细设置如表8所示。

表7 时间间隔-水位变化表

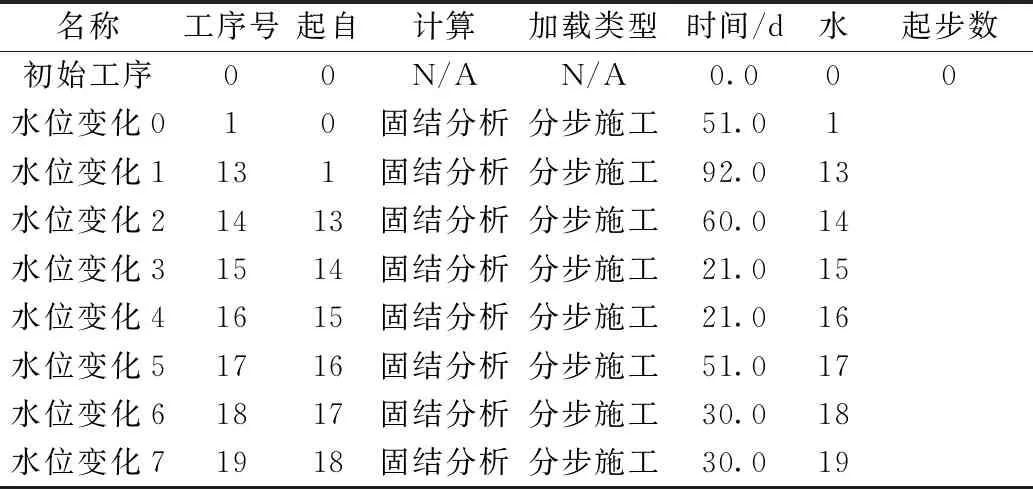
表8 分步施工工序设置表

本次数值模拟是在模拟BC792点从2018年11月3日到2019年10月25日期间所发生的沉降变形量，时长共356 d。图9所示A点即为BC792位置，B、C、D、E为其他表层监测点位置。

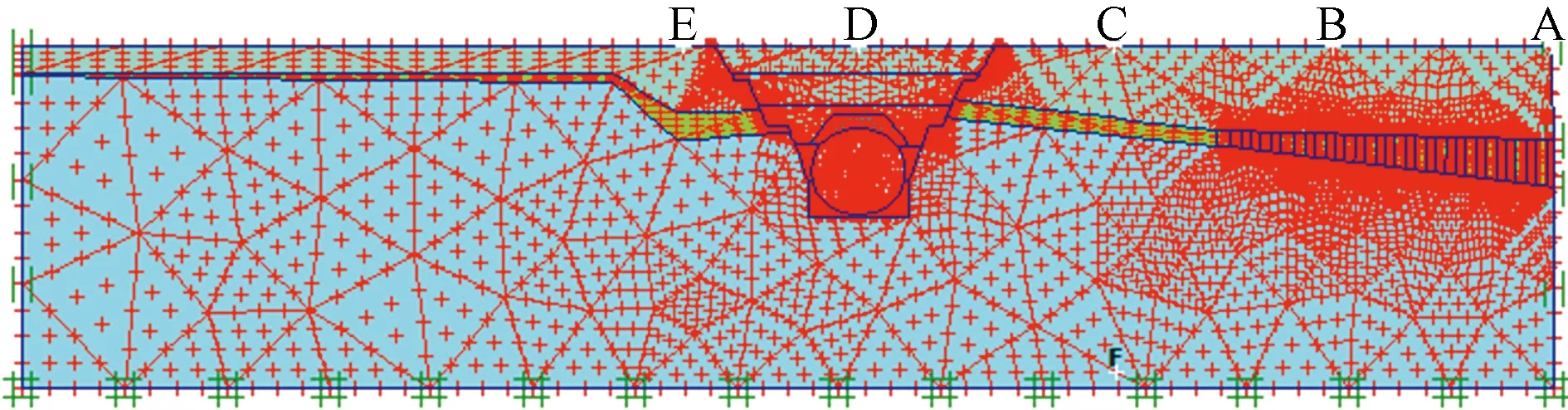
图9 数值计算选取点A(BC792)

完成设置后开始进行数值模拟计算，变形的网格图和阴影图如图10所示。

从图10可以看出从A点到B点到C点，其沉降变形越来越小。归结原因，距离A点越近，砂泥岩填料的高度越高，软土的厚度也越厚，随着地下水位线的变化其沉降变形越大。A点、B点、C、D点的变形-时间曲线如图11所示，从下往上依次为A、B、C、D点曲线。

图10 东区1-1′剖面沉降变形网格和阴影图

图11 A、B、C、D的变形时间曲线图

根据监测数据BC792从2018年11月3日到2019年10月25的实际变形量为81.2 mm，数值模拟数值73.1 mm，误差在允许范围内。

4.4 实测值、理论计算与数值计算对比

飞行区大铁(东区)的表层监测点实测沉降变形、理论计算沉降变形、数值计算沉降变形值得对比如表9所示。

从表9可以看出，考虑湿化变形的分层总和法的差值占比为-12.64%～17.47%，数值模拟的误差占比为-11.97%～8.28%，其模拟效果相对较好。

表9 实测值、理论计算和数值模拟计算对比表

综上所述，成都天府国际机场新近回填区域填料由于没有经受降雨的影响且填筑高度高、未完成固结沉降，为确保湿化变形对工程不造成太大危害，选用理论公式计算、数值模拟、监测数据进行湿化变形分析，结果证明理论公式计算和数值模拟的可靠性，可以用来模拟湿化变形的，同时也证明了考虑湿化变形的分层总和法计算方法的适用性。