一种双阶段多智能体路径规划算法

2021-09-09李庆华王佳慧李海明

科学技术与工程 2021年22期

李庆华, 王佳慧, 李海明, 冯超*

(1.齐鲁工业大学(山东省科学院)电子信息学院(大学物理教学部)，济南 250353； 2.济南市人机智能协同工程实验室，济南 250353；3.齐鲁工业大学(山东省科学院)电气工程与自动化学院，济南 250353 )

随着无人化工作的复杂性、动态性增强，多智能体路径规划问题逐渐成为研究热点，诸多学者对这一领域做了有益的探索[1-2]。多智能体路径规划算法的定义为：在响应规划请求时，要求每个智能体均可规划出连接各自起点和终点的路径，同时确保智能体之间无碰撞，且与障碍物无碰撞。根据多智能体协调控制方式可分为耦合式方法和解耦式方法。

耦合式方法是将所有智能体视为一个整体对其进行路径规划，寻找无碰撞路径。Ferreira等[3]提出一种双向通讯链路的思想，通过建立包含地层几何形状及其位置的势能场来实现水下多机器人的协调。Liu等[4]提出一种基于A-Star(A*)算法和包含环境表示的遗传算法实现多机器人任务分配和路径规划。耦合式方法[5]需要共享空间，并将多智能体的信息传递给一个系统进行控制，不需要特定的协作算法，但该类算法普遍存在配置空间维度高、计算复杂的问题。

解耦式方法是将每个智能体视为独立个体，通过构建协作算法修改已规划的独立路径，从而获取无碰撞路径。Settembre等[6]提出了一种分散的协作态势评估方法，当一个机器人局部认为某个特定的计划应该被执行时，就会发送该计划的建议给其团队成员，该算法成功地平衡了协作感知和共享大量信息的成本。晁永生等[7]提出一种两阶段解耦方法，首先利用A*算法为每个智能体规划出在静态环境下无碰撞的路径，再通过修改不同机器人的冲突路径实现机器人间的协调配合。该方法提高了搜索效率，但该方法的不足在于A*算法不能保证找到一条最短路径[8]。解耦式方法存在智能体间相互干涉，协作算法可实现局部最优，但无法确保全局最优[8]。

目前常用的路径规划算法主要有：通过模拟自然进化过程搜索最优解的遗传算法；通过搜索势能函数下降方向寻找路径的人工势场法(artifical potential field method, APFM)；基于启发函数搜索的A*算法；基于采样搜索的概率路线图(probabilistic roadmap，PRM)方法。诸多学者对路径规划算法继续探索[9-10]。在规划路径时，遗传算法具有良好的全局搜索能力，但搜索速度较慢[11]；人工势场法能够得到最优路径且路径平滑，但其易陷入局部最优[8]；A*算法基于启发式函数可快速地导向目标节点[12],但其路径并不是最优[8]。PRM算法是概率完备的但不是最优[13]。相对于其他算法，快速扩展随机树(rapidly exploring random trees，RRT)算法[14]计算复杂度较低，在不使用配置空间中障碍物显式信息的情况下找到解决方案，但它不能确保路径搜索的渐进最优[15]。

针对此问题，Karaman等[15]提出了RRT*算法，通过增加选择父节点和重布线过程，保证快速找到初始路径，并随着样本数量的增加对路径进行优化。该方法具有概率完备性，同时确保了路径搜索的渐近最优。RRT*算法在理论上可以得到一个最优解，但在有限时间内由于算法收敛速度慢，最优解的计算不能在有限时间内完成。Nasir等[16]引入智能采样和路径优化策略，提出了RRT*-SMART(smart rapidly-exploring random trees star)算法，加快算法的收敛速度。RRT*-SMART算法在找到起点和终点间可行路径后，从子节点开始不断判断是否可直接连接先辈节点。在优化过程中，障碍物附近如果出现无法直接优化的锚点，在锚点附近增加采样，找到更优路径，但该算法的环境自适应性差。Noreen等[17]提出基于连通区域、目标有界采样和路径优化的RRT*-AB(RRT*-adjustable bounds)算法。在连通区域的边界上进行目标偏置有界抽样，寻找初始路径。这种采样策略降低了RRT算法的采样盲目性。一旦找到路径，通过节点抑制和集中有界抽样的方法逐步优化路径。张伟民等[18]提出一种基于目标约束采样和目标偏置扩展的改进RRT*(goal-bias constrained sampling and extending RRT*，GCSE-RRT*)算法。在采样阶段设置目标偏置概率，在一定概率下选择目标点作为采样点，在随机采样时对采样点位置约束，提高采样阶段的目标导向性；扩展新节点时由随机点和目标点共同决定，加快算法搜索速度。相对来说，GCSE-RRT*算法提高了节点利用率，占用内存更少，并且运行时间更短，但规划出的路径不是最优。

现基于回溯思想提出一种改进的RRT*(back tracking RRT*，BT-RRT*)算法，并结合自适应局部避障策略解决多智能体的路径规划问题。算法分为两个阶段，全局路径规划阶段，各智能体在不考虑其他智能体的前提下，在静态环境中规划各自无碰撞路径；在协作避障阶段，智能体沿着已规划好的路径移动，基于自适应局部避障策略，实时对动态障碍物和其他智能体进行避障。

1 基础知识

给定工作空间W，其中障碍物区域为Wobs，无障碍物区域为Wfree。在RRT*算法中，构建的树为T=(V,E)，其中V为节点集合，E为连接节点的边集合。定义Ψ(q1,q2)为节点q1、q2间的路径，c(q1,q2)为随机树中两个节点q1、q2之间的路径成本，c(q,T)为起始点朝向节点q的路径成本，路径成本用欧氏距离来计算：

(1)

式(1)中：(x1,y1)、(x2,y2)为节点q1、q2的坐标。

定义1：父节点的阶。将距离新节点最近的节点定义为1阶父节点，则上一父节点为其2阶父节点。则经m次回溯后，新节点可回溯至其m阶父节点。

1.1 RRT*算法

扩展树以起始点qinit为根节点开始扩展，首先在整个搜索空间中采取随机的方式生成随机点qrand，然后遍历当前已有的树节点，从中寻找距离qrand最近的节点qnearest，在点qnearest处向qrand延伸步长p后得到新节点qnew。如果新节点qnew在无障碍区域，则以新节点为圆心，r为半径(r>0)，得到落在这个区域内的节点的集合Q={qnearest,q1,q2}，如图1(a)所示。如图1(b)所示，遍历集合内所有点，选择起始点qinit到达新节点qnew时的路径成本最小的节点为新节点qnew的最佳父节点，从而进行重新布线。最后为集合内其他节点进行重新布线，进一步使得随机树节点间连接的代价尽量小，如图1(c)所示，选择节点q1、q2的最佳父节点，达到优化效果。起始点朝向节点qnew的成本代价与qnew、q2之间的路径成本的和小于起始点朝向节点q1的成本代价与q1、q2之间的路径成本的和，因此节点q2的最佳父节点为qnew，如图1(d)所示。

图1 RRT*算法重新布线过程

1.2 BT-RRT*算法

RRT*算法是在RRT算法的基础上添加一个寻找最佳父节点的过程，并对随机树重新布线，从而在给定环境中生成较优路径。为了缩短RRT*算法的路径代价和计算成本，提出了回溯布线法。表1给出了BT-RRT*算法的主要步骤，在给定无障碍物区域中随机采样一个节点qrand，由Nearest函数得到随机树T中距离随机点qrand最近的节点qnearest，再由Steer函数获得沿qrand方向上距离节点qnearest长度为p的节点qnew，确定新节点后，若新节点在无障碍区域，将使用Rewire函数对随机树回溯布线，经过多次迭代后，逐渐从无障碍区域优化出一条较优路径。

表1 BT-RRT*算法

表2给出回溯布线的过程，一旦确定新节点qnew在无障碍物区域，将对从起始点qinit到新节点qnew的路径回溯布线，被检查节点qc从qnearest的父节点qnearest-parent开始向起始点qinit移动，检查每个节点与新节点qnew间的路径Ψ(qc,qnew)是否在无障碍区域，直到无冲突条件失败，停止回溯，新节点qnew的最佳父节点qnew-parent为回溯路径中最后一个无碰撞节点。图2所示为回溯布线前后树结构的变化。如图2(b)所示，基于三角形不等式的概念对路径重新布线，边e3总是小于e1和e2的和，因此存在一条较短的路径e3，重新布线后的路径如图2(c)所示。

由定义1可知，点1为1阶父节点，点2为2阶父节点

表2 回溯布线

1.3 回溯布线的复杂度

推论1：对于任一新节点qnew，随机变量A表示每次需回溯的次数，m表示不发生碰撞的次数，新节点可回溯至其m阶父节点，则有P(A1-(1/2)m。

证明：假设障碍物在工作空间内是均匀分布的，则单次回溯与环境产生无碰撞的概率P(A=1)=1/2。则有

P(A=m)=(1/2)m

(2)

P(A1-(1/2)m

(3)

定义2(可忽略函数[19])：存在一个函数f:N→R，如果满足以下条件：对于整数c>0来说，存在一个正整数nc，对于n>nc的整数来说，有关于n的多项式|f(n)|<1/nc，则该函数为一个可忽略函数，常用negl(n)表示。

推论2：对于每个新节点qnew可回溯次数A<10的概率接近1。因此A/n=negl(n)，其中n为全部可回溯的节点数量。所以BT-RRT*算法的回溯布线过程中所增加的碰撞检测复杂度可被忽略，其整体复杂度小于RRT*算法的复杂度。

2 多智能体路径规划

数学符号采用通用的表示方法，表3给出了多智能体路径规划中特殊符号的含义。

表3 符号含义

2.1 动态环境下多智能体路径规划算法

首先，在不考虑其他智能体的前提下，在静态环境中为各智能体规划无碰撞路径。然后，各智能体以固定步长ε沿其无碰撞路径从起点向目标点移动。在各智能体移动过程中，结合距离传感器获得的局部信息和避障策略完成局部避障，其中局部避障包括对动态障碍物的避碰和对其他智能体的避碰。

图3为算法的具体步骤，首先初始化有关参数，包括各智能体的起始点Si、目标点Gi、探测半径R及移动步长ε。在静态环境中利用BT-RRT*算法规划各自无碰撞路径Pathi，此时不考虑其他智能体。各智能体在以步长ε执行路径过程中利用距离传感器获得其与动态障碍物和其他智能体之间的距离Li，同时实时记录各智能体的位置。若距离传感器探测范围内存在障碍物，则根据局部避障策略避开障碍物，否则，各智能体在原规划路径匀速移动。若所有智能体达到目标点，则算法终止。

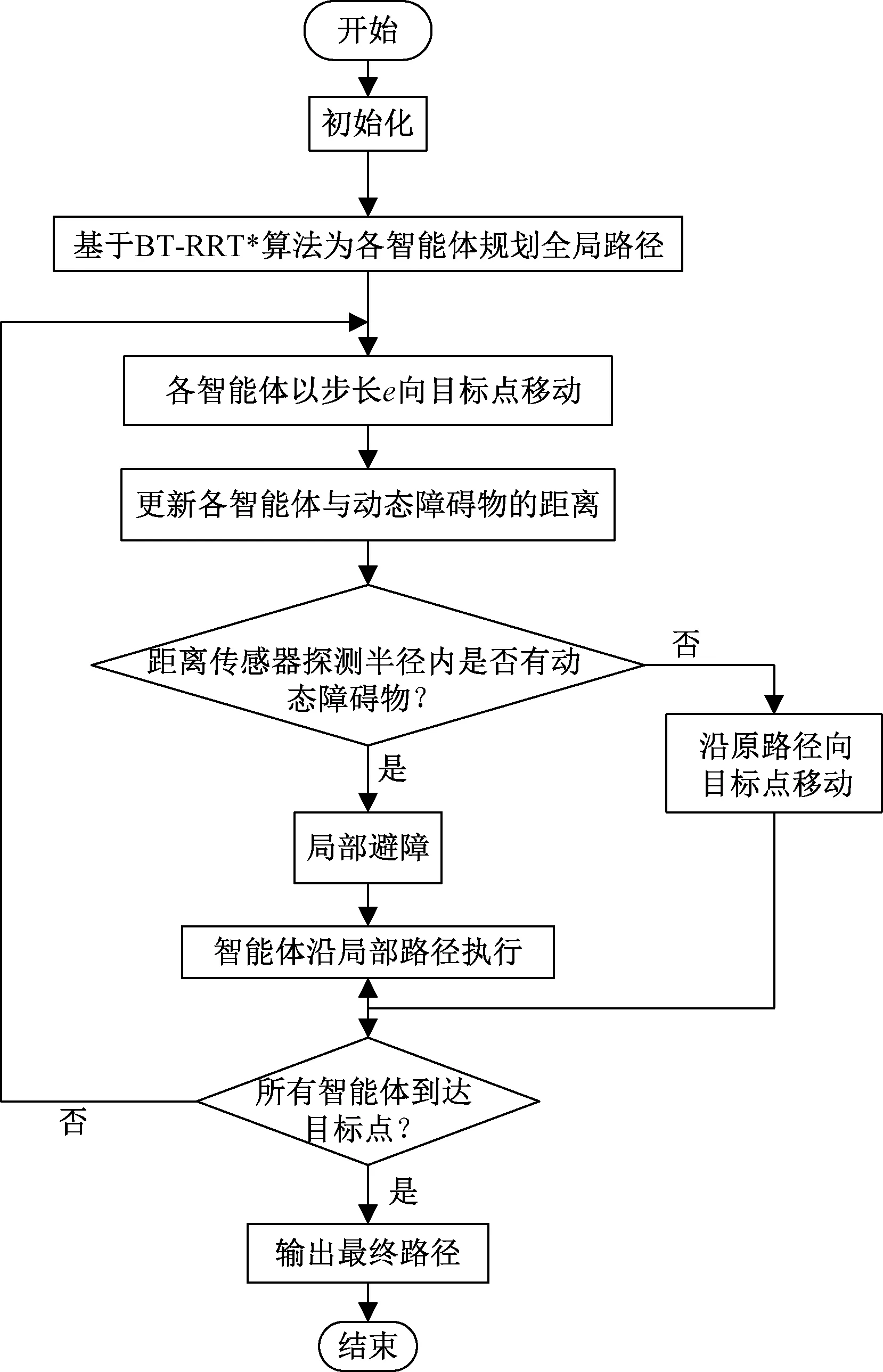
图3 多智能体路径规划算法

2.2 自适应局部避障策略

定义3(任务优先级)：在仿真实验中任务优先级预先自定义，智能体所承担的任务越重要，智能体的优先级越高。

智能体间的协作以局部路径重规划方式为主。距离传感器的探测半径为

R=Mn/10

(4)

其中环境尺寸为Mn×Mn像素。传感器的探测半径越大局部避障效果越好，但增加重规划时间。

根据任务重要程度确定智能体的协作优先级，将其他智能体视为动态障碍物，若两智能体间距离小于距离传感器探测半径。则根据各智能体的优先级和局部避障策略完成智能体间协作。优先级高的智能体在原路径向目标点移动，优先级较低的根据避障策略完成局部避碰。

图4为局部避障过程，利用距离传感器获得各智能体与前方动态障碍物的距离Li，将动态障碍物的避碰分为两个阶段，当R/2

图4 局部避障算法

3 仿真实验

对提出的算法在多智能体全局路径规划时的有效性进行仿真验证。实验空间尺寸为200×200像素。实验过程中将智能体看作质点处理。仿真实验平台及配置为：MATLAB R2018b，64位Windows10，处理器Intel(R) Core(TM) i5-8265U，CPU主频1.6 GHZ。

3.1 全局路径规划阶段

在基于采样思想所构造的RRT*路径规划算法中，算法主要由两部分组成：首先构造快速扩展随机树用以表示地图，快速扩展随机树是由多个无碰撞节点，及节点间的边构成，节点数量由RRT*算法的迭代参数决定。随后基于该树形结构，依据代价函数进行路径搜索获取规划后的路径。

定义4(路径节点)：在RRT*算法中，构成规划路径的无碰撞节点定义为路径节点。

定义5(路径节点数量)：任意一条路径是由该路径上的无碰撞快速扩展随机树节点，及相邻节点间的无碰撞边构成，这些无碰撞节点的个数称为该条路径的路径节点数量。

在全局路径规划阶段，使用RRT*算法、GCSE-RRT*算法和BT-RRT*算法在3种不同环境下对多智能体初始路径规划进行仿真对比。图5～图7分别表示2个智能体、3个智能体、4个智能体路径规划结果，图中均已标明各个智能体的起始点、目标点，其中黑色为障碍物区域。

图5 2个智能体路径规划结果

图6 3个智能体路径规划结果

图7 4个智能体路径规划结果

从路径长度、规划时间两方面进行对比，对比得到的仿真结果如表4所示。智能体数量为2时，相同环境中BT-RRT*算法比RRT*算法节省23.7%的时间，路程缩短13.4%；比GCSE-RRT*RRT*算法节省5.9%的时间，路程缩短5.2%。智能体数量为3时，相同环境中BT-RRT*算法比RRT*算法节省29%的时间，路程缩短16.4%；比GCSE-RRT*RRT*算法节省10.4%的时间，路程缩短14.1%。智能体数量为4时，相同环境中BT-RRT*算法比RRT*算法节省31%的时间，路程缩短10%；比GCSE-RRT*RRT*算法节省10%的时间，路程缩短5.5%。

表4 算法性能比较

基于回溯布线思想在添加新节点向起始点回溯，不仅降低了路径成本，也降低了路径点的数量。在路径规划过程中路径点以坐标的形式实时保存，占用一定的内存数量。给定环境尺寸为200×200像素，单个坐标(x,y)占用内存为16 bit，则整体算法占用内存为bn=16Pnbit，其中Pn为路径节点数量。在相同环境下BT-RRT*算法相较于RRT*算法和GCSE-RRT*算法路径点明显减少。因此BT-RRT*算法占用内存较少。BT-RRT*算法不受环境、智能体数量的约束，随智能体数量的增加，其在路径长度，规划时间、路径节点方面均表现出优势，因此本文提出的算法适用于多种不同环境，获得的路径更短，搜索路径时间更短。

3.2 动态环境下多智能体路径规划仿真

对提出的动态环境下多智能体路径规划算法的有效性进行仿真验证，如图8所示，环境尺寸为200×200像素，其中，动态障碍物在环境中以随机的方向移动，智能体移动步长为2，距离传感器探测半径为20单位像素。根据定义3，4个智能体优先级定义为：智能体1>智能体2>智能体3>智能体4，说明智能体1的所承担的任务更重要。在静态环境下，智能体的全局规划路径用蓝色虚线表示，在路径执行过程中，各智能体根据避障策略避开动态障碍物和其他智能体，各智能体的最终路径用红色实线表示。实验表明，智能体可以避开动态障碍物，同时避开其他智能体，获得较优路径。