基于多分辨率生成对抗网络的空间数据不确定性重建方法

管其杰，张 挺*，李德亚，周绍景，杜 奕

（1.上海电力大学计算机科学与技术学院，上海 200090；2.上海第二工业大学工学部，上海 201209）

0 引言

空间数据是数据的一种特殊类型，兼具结构性和随机性［1］。目前，重建大范围、真实、有效的空间数据比较困难，主要原因在于科学实验和勘探开发费用高［2］。

数据插值成为重建空间数据的一个有效手段［3］。插值方法分为“确定”性插值方法和“不确定”性插值方法。不确定性插值方法的不确定性主要表现在插值结果的不确定性和多样性，但是这些结果是对训练数据的统计特征的呈现，具有较强的指导意义［4］。不确定性插值方法主要包括克里金（Kriging）方法和随机模拟方法。多点统计法（Multiple-Point Statistics，MPS）是目前随机模拟的主流，其特点是基于训练图像（Training Image，TI）进行建模，本质上是基于概率统计思想进行特征提取和特征复制。近年来，MPS得到了广泛应用并发展了一些变体，如SNESIM（Single Normal Equation SIMulation）［5］、FILTERSIM（FILTER-based SIMulation）［6］、DS（Direct Sampling）［7］等。SNESIM算法通过统计待模拟点与周围条件数据点构成的数据事件在训练图像中出现的概率，利用马尔可夫蒙特卡罗法抽样，完成待模拟点的随机模拟。FILTERSIM算法引入了一系列不同方向的线性滤波器对训练图像进行过滤和分类。DS算法根据已知空间数据信息，通过计算距离选择已知区域中最佳匹配的训练模式作为待模拟点的模式。但是上述这些方法耗时较长且CPU占用率高。流行学习的应用是通过从高维空间中提取低维的流行结构实现对高维数据的降维，来提高重建的速度，但是本质上不能降低对空间训练数据的需求［2］。

作为机器学习研究的新领域，深度学习建立了一个可以模拟人脑进行分析学习的神经网络，在语音识别、计算机视觉、自然语言处理等方面得到广泛应用［8］。同时深度学习产生了若干分支，包括自动编码器、深度信念网络、卷积神经网络以及深度玻尔兹曼机等，在空间数据重建领域有着重要的应用，但这些方法存在数据收集和标记的成本过高、数据收集困难等问题［9］。生成对抗性网络（Generative Adversarial Network，GAN）［10］也是深度学习的一种流行方法。GAN是一种让两个神经网络相互博弈的非监督学习方法，它包含一个生成网络G（Generator）和一个判别网络D（Discrim inator）。生成网络G的思想是将一个噪声映射成一个逼真的样本，而判别网络D需要判断生成的样本是真还是假，GAN通过G和D的对峙来产生G的新框架。

相对于基于统计学方法的MPS方法通过捕获训练图像特征来完成图像重建，GAN能够利用多层神经网络对训练图像进行学习，自动获取抽象的特征，生成与真实数据分布一致的图像［11］。然而，应用于空间数据重建领域的GAN方法大多数都是在大型数据集上进行训练的［12-14］，这对数据集提出了严苛的要求，必然对训练数据不易获取的任务造成困难，并且导致训练任务繁重，对训练环境的硬件要求较高。在某些情况下，最好是在少量图像上训练生成模型，或者在有限的情况下，在单个图像上训练。由于单幅图像中切片的经验熵小于图像分布中切片的经验熵，因此学习单幅图像中切片的统计和分布能够提供较好的先验知识［15］。最近的研究也表明，通过自监督学习和数据增强，在单幅图像上训练一个模型可以学习到足够的特征信息［16］。但是GAN的感受野有限，因此能够提取的图像特征范围也受到一定限制。如果能够提取单幅训练图像在不同尺度或不同分辨率情况下的特征，利用多个特征进行图像重建，将能够获得更好的图像重建结果。因此，本文提出一种基于多分辨率GAN的空间数据重建方法（称之为MultiGAN）。

MultiGAN的目标是建立一个能捕捉到不同分辨率下空间数据特征的生成模型。为了充分捕捉训练图像的结构信息，MultiGAN构建了一个金字塔结构，该金字塔结构是不同分辨率的训练图像形成的GAN，每个GAN在相应的分辨率尺度上学习训练图像的结构信息，即在高分辨率训练图像上捕捉全局特征，在低分辨率训练图像上捕捉局部特征和细节。实验结果表明，相对于普通的GAN模型，MultiGAN可以从单个训练图像中产生高质量的重建图像，并且重建时间较短，因此具有较高的重建效率。

1 本文方法的基本原理

1.1 网络模型

本文模型是GAN的一个变体。其中，GAN是一种非监督学习网络，包含相互博弈的两个神经网络：生成器G和判别器D。G和D这两个网络相互作用并不断调整，最终目标是使判别器无法判断生成器的输出是否是真实样本，从而实现模型学习到训练图像特征的目的。

生成器G和判别器D之间的博弈是由GAN的最小成本函数决定的：

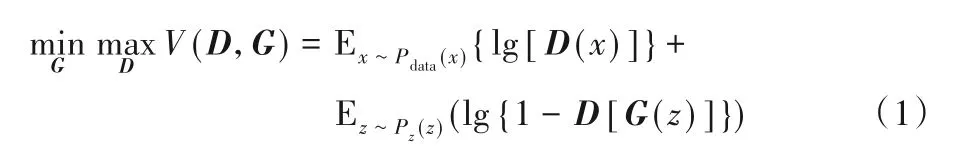
其中，D(x)指的是x来自真实数据分布Pdata（x）的概率，而D[G(z)]指的是假样本G(z)产生的概率，E代表期望值。在实际应用中，GAN有时出现训练较为困难、生成器和判别器的损失无法指导训练过程以及生成的样本缺乏多样性等问题［17］，因此出现了一些GAN变体去改善这些问题，例如文献［17-18］从理论和实验两个方面分析了GAN，并对其进行了改进，提出了WGAN（Wasserstein GAN）。WGAN通过权重剪切独立地限制每一个网络参数的取值范围，确保训练过程中判别器参数有界，不会因为样本的不同给出差别巨大的分数值。但是实践过程中发现，WGAN的权重剪切的阈值很难设置合理，设置较小容易导致梯度消失，设置较大会导致梯度爆炸。因此文献［19］提出WGAN-GP（WGANwith Gradient Penalty），通过在判别器的损失函数中加入梯度惩罚项来改善WGAN的问题。WGAN-GP的目标函数为：

1.2 多尺度多分辨率结构

由于受计算资源和网络结构的约束，网络的感受野有限，如果直接对训练图像进行训练，重建后的图像实际上只重建了训练图像上有限大小的结构特征，难以兼顾全局和局部特征，因此本文提出在多种分辨率情况下通过固定大小的感受野来扫描不同分辨率的训练图像，以实现训练图像不同尺度特征的提取。将训练图像按不同的尺度进行缩放，形成多分辨率训练图像用于阶段训练，利用固定大小的感受野来捕获不同分辨率下训练图像的结构信息。图1所示为捕获不同分辨率的训练图像信息示意图，图中显示了3个尺度的训练图像。

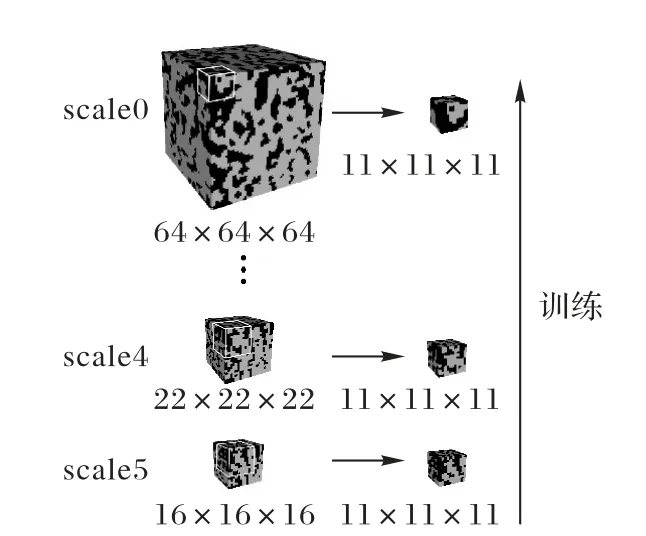
图1 提取不同分辨率训练图像信息的示意图Fig.1 Schematic diagram for extracting training image information at different resolutions

从图1可以看出，在低分辨率的情况下，模型主要学习图像的整体分布信息；而在高分辨率的情况下，能够重点学习图像的细节和纹理信息。不同分辨率训练图像的大小为：

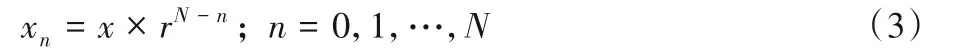
x为输入图像大小，N为尺度数量，r为尺度缩放因子，表示为：

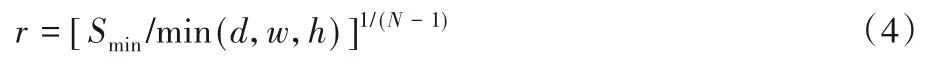
其中：Smin为设置的最低分辨率下训练图像的大小，d、w和h分别为输入图像x的深度、宽度和高度大小，min（d，w，h）为输入图像3个维度大小的最小值。利用尺度缩放因子对输入图像进行下采样获得不同分辨率的训练图像进行训练，这一多分辨率结构称之为“金字塔结构”，图2所示为N+1尺度的金字塔结构。

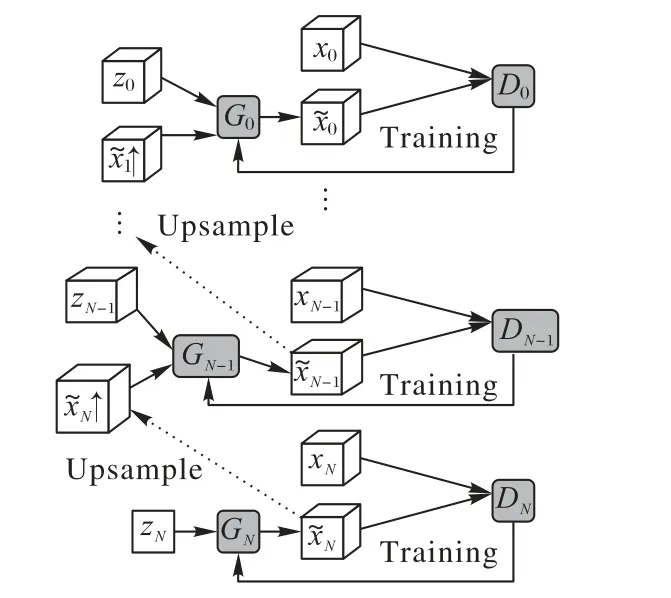
图2 N+1尺度的金字塔结构Fig.2 Structureof pyramid with N+1 scales

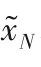
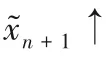
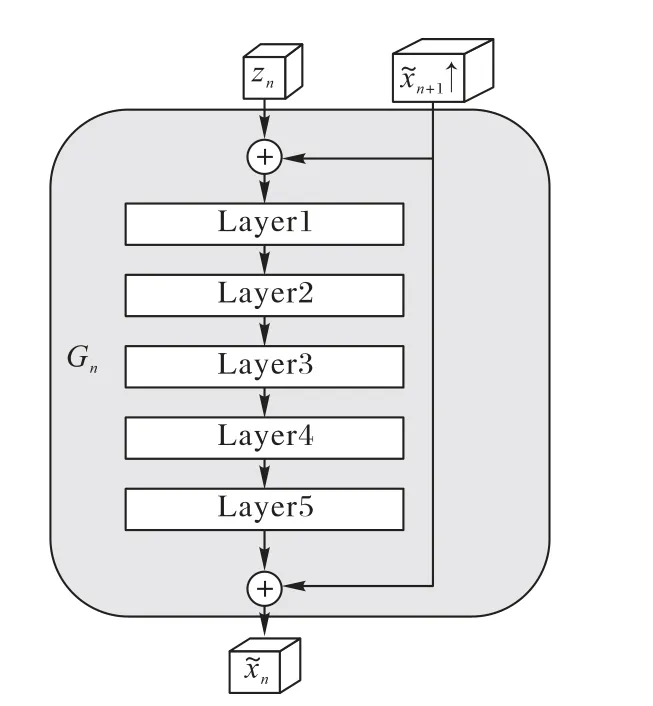
图3 Gn的结构（0≤n≤N-1）Fig.3 Structureof Gn（0≤n≤N-1）

1.3 模型训练

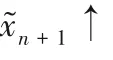
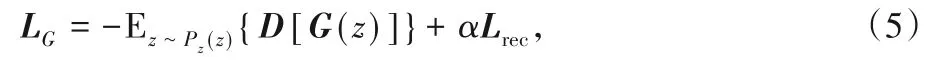
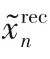
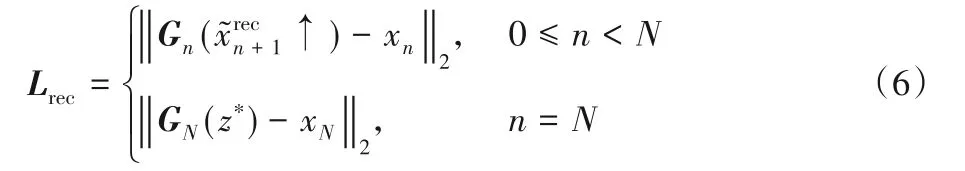
训练过程中发现，过高的学习率会导致图像的过度拟合和模式崩溃，而过小的学习率则会导致生成的图像纹理细节不明显。为了平衡学习率与重建图像效果，模型使用Adam优化器［20］来调整超参数。Adam优化器不仅可以计算出各参数的自适应学习率，还可以通过训练数据的不断迭代使网络权重自动更新，保证了训练的效率以及重建图像的质量。

2 实验结果

为了评估重建空间数据的效果，选择与MPS方法中SNESIM、FILTERSIM和DS三种代表性算法以及应用于空间数据重建的GAN［13］方法进行对比，对重建图像的变差函数、孔隙度、多点连接性、CPU、GPU和内存使用情况等方面进行对比分析。MultiGAN模型使用五层网络，金字塔结构为6层，训练图像大小由小到大为：16×16×16、22×22×22、28×28×28、37×37×37、49×49×49、64×64×64。卷积核大小为3×3×3，感受野大小为11×11×11，激活函数LeakyReLU的负数部分斜率为0.2。

2.1 重建图像的比较

本实验拟采用真实岩石数据作为空间数据重建的数据源，由于真实岩石的内部孔隙数据难以用数学公式或者某种定量的语句描述，故岩石的孔隙分布具有很强的不确定性特征，适合采用不确定性重建方法重建孔隙结构。使用纳米CT扫描技术获取分辨率为64 nm/体素的真实页岩体数据。从真实页岩数据截取尺寸为64×64×64体素的立方体作为训练图像，其外表面、剖面图（X=32，Y=32，Z=32）以及孔隙结构如图4（a）所示。图4中的页岩数据由骨架和孔隙两部分组成，其中灰色区域代表骨架，黑色区域代表孔隙空间。从图4（a）可以看出，训练图像的孔隙呈现不规则且长连通的特点。图4还显示了使用SNESIM、FILTERSIM、DS、GAN以及MultiGAN方法重建的图像。可以看出，五种重建方法均基本再现了训练图像不规则且长连通性的孔隙空间，但是MultiGAN重建图像与训练图像最为接近。

图4 训练图像和不同方法重建图像的外表面、剖面图以及孔隙结构Fig.4 Outside surface，profile and pore structures of training image and images reconstructed by different methods

2.2 孔隙度对比

岩石孔隙度被定义为孔隙体积V与岩石总体积Vp的比值，用于表示岩石存储流体的能力，用符号ϕ表示，定义为：

训练图像的孔隙度为0.228 2，分别利用SNESIM、FILTERSIM、DS、GAN以及MultiGAN重建10幅图像，孔隙度结果如表1所示。从表1可以看出，MultiGAN重建图像的孔隙度更接近训练图像孔隙度。

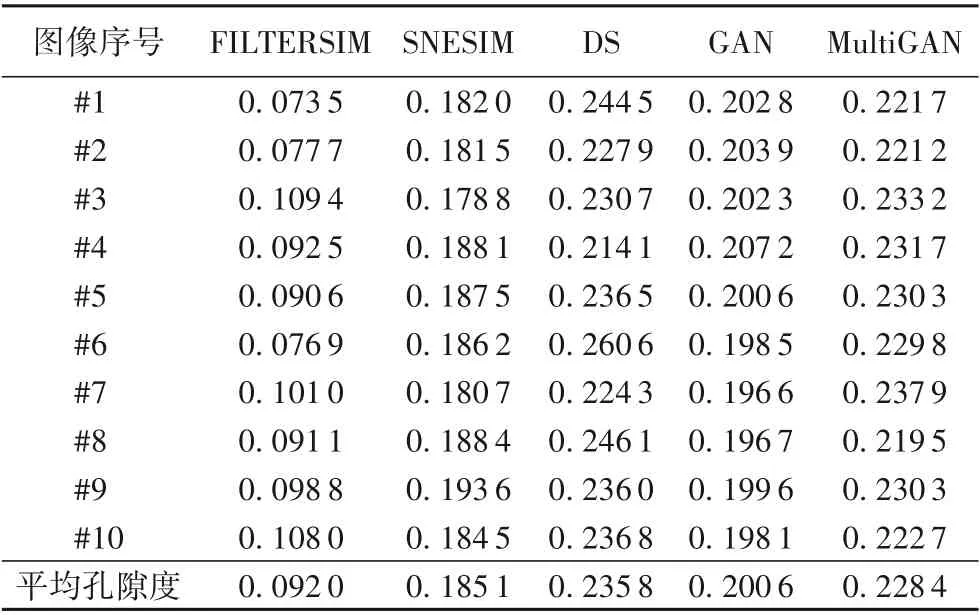
表1 SNESIM、FILTERSIM、DS、GAN和MultiGAN重建10幅图像的孔隙度Tab.1 Porositiesof 10 images reconstructed by SNESIM，FILTERSIM，DS，GAN and MultiGAN

2.3 变差函数对比

变差函数反映了在一定方向上的空间变量的相关性和变异性，常用来作为评估重建效果的工具，定义如下：

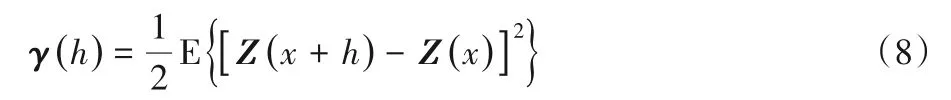
其中Z(x)是位置x处的属性值，h是位置x和x+h之间的滞后距离，E是数学期望值。如果两幅图像在同一方向上有相近的变差函数曲线，则两幅图像在该方向上具有相近的结构特征；反之，两幅图像在该方向上结构差异较大。图5是训练图像和SNESIM、FILTERSIM、DS、GAN以及MultiGAN方法重建图像的变差函数曲线。横轴表示滞后距离，相邻体素之间的距离为1，纵轴分别表示3个方向的变差函数值。

从图5中可以看出，MultiGAN重建图像与训练图像的变差函数曲线更接近，说明MultiGAN重建效果更好。

2.4 多点连接性对比

变差函数可以衡量空间两点间的变异性，为了同时衡量空间多点之间的连接性，可以定义如下的多点连接性函数（Multiple-Point Connectivity，MPC）：

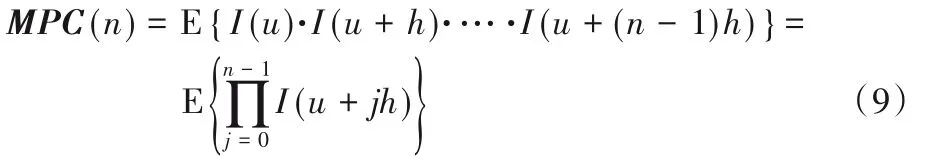
其中：h为滞后距离，n为一个方向上的节点数，E为数学期望值，u表示空间某点位置。指标变量I（u）具有两个属性值：当页岩图像中某个位置为孔隙空间时，I（u）=1；否则I（u）=0。

图6是训练图像和使用SNESIM、FILTERSIM、DS、GAN以及MultiGAN方法重建图像的MPC曲线图。从图6中可以看出，MultiGAN方法重建图像与训练图像的MPC曲线最接近。

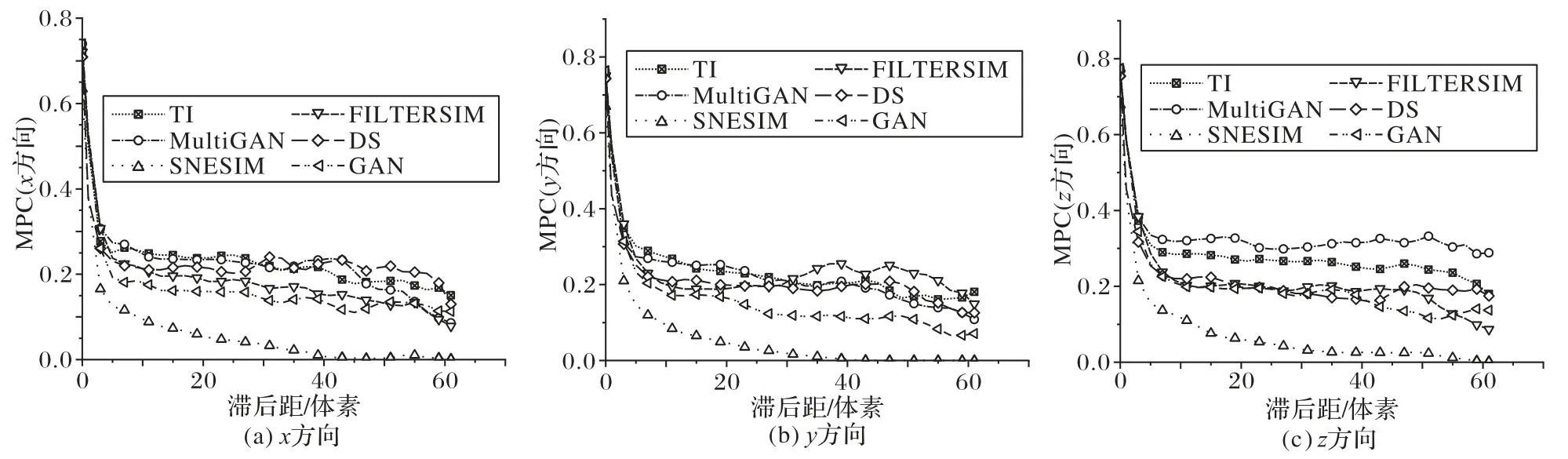
图6 重建图像和训练图像的MPC曲线Fig.6 MPC curvesof training imageand reconstructed images

2.5 内存和运行时间对比

实验硬件环境为Intel Core i7-7800X CPU、NVIDIA GeForce RTX 2080 Ti GPU和24 GBRAM。另外，本文的GAN和MultiGAN基于PyTorch的深度学习框架运行。SNESIM、FILTERSIM和DS使用了基于MPS的软件框架运行。对SNESIM、FILTERSIM、DS、GAN和MultiGAN算法在CPU/GPU/占用内存方面进行比较。为了获得较为客观的数据，根据10次重建的重建结果进行比较，结果如表2所示。总重建时间在表2由两部分组成：第一次重建时间和其余九次重建总时间。可以看出，尽管在“第一次重建时间”项中，SNESIM，FILTERSIM和DS所花费的时间少于GAN和MultiGAN，但它们在“其余九次重建总时间”中却花费了更多时间。这是由于SNESIM、FILTERSIM和DS三种方法每次重建时都需要重新对训练图像进行扫描以获取其结构信息，这些信息存储在内存中而不是文件内，一次重建结束后上述结构信息即被清除，而且即使能够将这些信息存储在文件内，整个重建过程也会因为存储结构非常庞杂而耗时较长；而GAN和MultiGAN在第一次重建后会将训练好的模型参数保存到文件中，而且参数储存结构相对简便，因此比传统MPS方法重建用时少。对比GAN和MultiGAN，可以看出MultiGAN在重建效率上优于GAN。可见，如果MultiGAN在后继重建过程中重复利用第一次重建后保存的模型参数，将对后继重建有很好的加速作用，因此比经典的不确定性插值方法具有更好的应用前景。同时，MultiGAN具有更低的CPU使用率，原因是深度学习及其相关算法的快速发展，使得MultiGAN等可以结合使用CPU和GPU，提升了GPU利用效率，降低了CPU的工作负载。尽管MultiGAN内存峰值较高，但是随着计算机硬件的发展，这样的内存峰值不会造成较大的问题。

表2 不同重建方法的CPU使用、占用内存峰值、总运行时间比较Tab.2 Comparisonsof CPU usage，memory peak usageand total running timeof different reconstruction methods

3 结语

本文提出了一种基于多分辨率GAN的空间数据不确定性重建方法，该方法以真实的空间数据作为训练数据，通过金字塔结构学习训练数据的全局和局部特征。训练结束后的模型可以保存下来，便于之后直接输入噪声进行重建。目前，一些不确定性插值方法被广泛应用于空间数据的重建。例如，使用MPS可以进行空间数据重建中的油藏模拟，但是时间较长，效率较低；利用流形学习进行空间数据模拟本质上是对数据进行降维，不能从根本上减少对空间训练数据的需求；一些其他深度学习方法可用于空间数据模拟，但是需要大量的空间数据训练集，因此适用性受限。而本文使用单幅训练图像创建的多分辨率结构可以在使用少量训练数据的情况下完成重建。

实验结果表明，与一些经典不确定性插值方法相比，该方法在运行效率上表现更优，并且重建图像质量更高。与GAN方法相比，MultiGAN只需要很少的训练数据即单个训练图像，而同类GAN方法需要大量训练图像作为训练数据，实验结果显示了本文方法在重建效率和质量上更优。