基于有限元技术的某车用发电机分析

钱宇晨，曹若旸，张留铭，李长玉

（1.广州城市理工学院，广东 广州 510800；2.华南理工大学广州学院，广东 广州 510800）

前言

旋转机械发电机是利用机械能和磁能转换为电能的装置，在水电，风电及热电等领域应用广泛，尤其在风电领域取得了成功的应用，是未来风力电机组发展应用的一个主要研究领域，因此旋转机械发电机的研究和开发是发电机领域研究的难点和热点[1]。目前，依靠现有的经验和模型实验等传统设计方法来验证模型的合理性，不仅占用大量的研发时间和耗费大量资本，而且在优化设计和产品研发周期等方面都具有一定的局限性，很难从根本上实现直驱发电机的快速设计[2]。随着数值分析技术与计算机仿真技术迅速发展，许多实际工程应用设计问题得到了有效解决[3]。通过计算机数值模拟技术的引入，可以快速地实现产品的优化设计，并降低产品的研发成本，这样改变了以前的样机测试开发途径，转变成现在较为流行的虚拟样机研发方法[4]。本文利用有限元法分析具有永磁体的转子的应力分析及其圆周旋转运动在磁性材料的定子绕组中产生感应电动势，发现发电机产生的线圈电压与时间呈现函数相关特征的规律性。该有限元模型能够通过模拟材料参数，通过定义不同的绕组的匝数，转子的角速度，扇区数，绕组中导线的直径，研究发电机的长度对线圈产生电压的影响。

1 模型的搭建及选用材料

1.1 前处理的设置

此永磁发电机首先通过设置绕组中导线的直径、绕组中的匝数、转子的角速度、发电机的长度和扇区数，确定其基本参数。

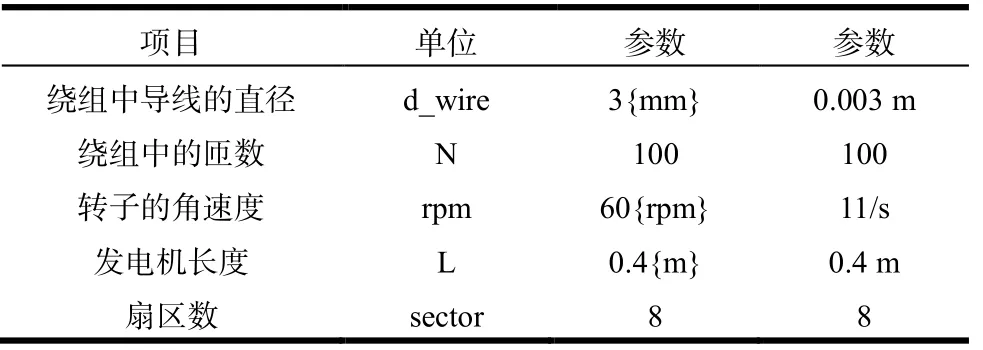
表1 模型的相关参数

1.2 模型的简化

此无刷直流电机为8极对称结构如图1所示，转子和定子的铁芯都是由层叠的饱和铁构成，转子齿则是由材料库中设置的初始材料制成的永磁体。当发电机的转速超过70 rpm时，无刷直流电机在t=0 s至t=0.25 s的时域内求解，此时转子达到与起始状态相同的对称状态。由于该几何存在扇区对称和相对于轴的镜面对称，因此可省去相同的几何结构，简化为图2所示的扇区几何模型。

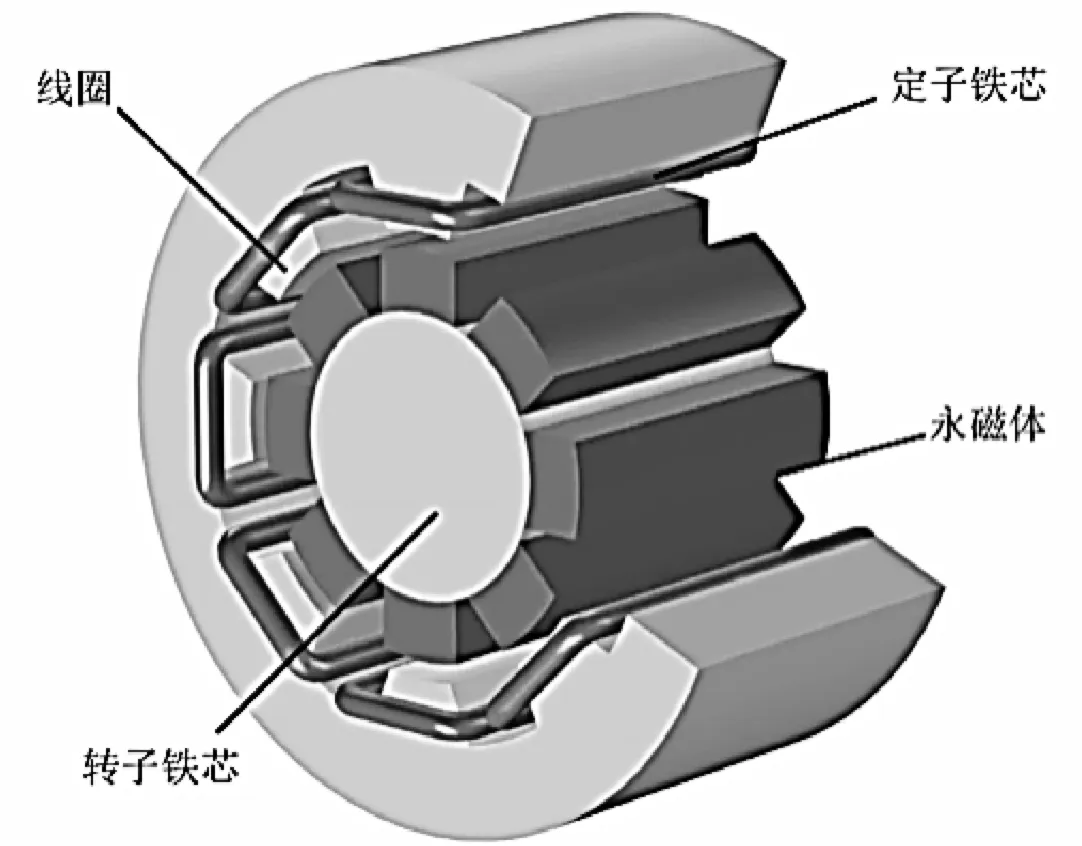
图1 无刷直流电机对称结构图

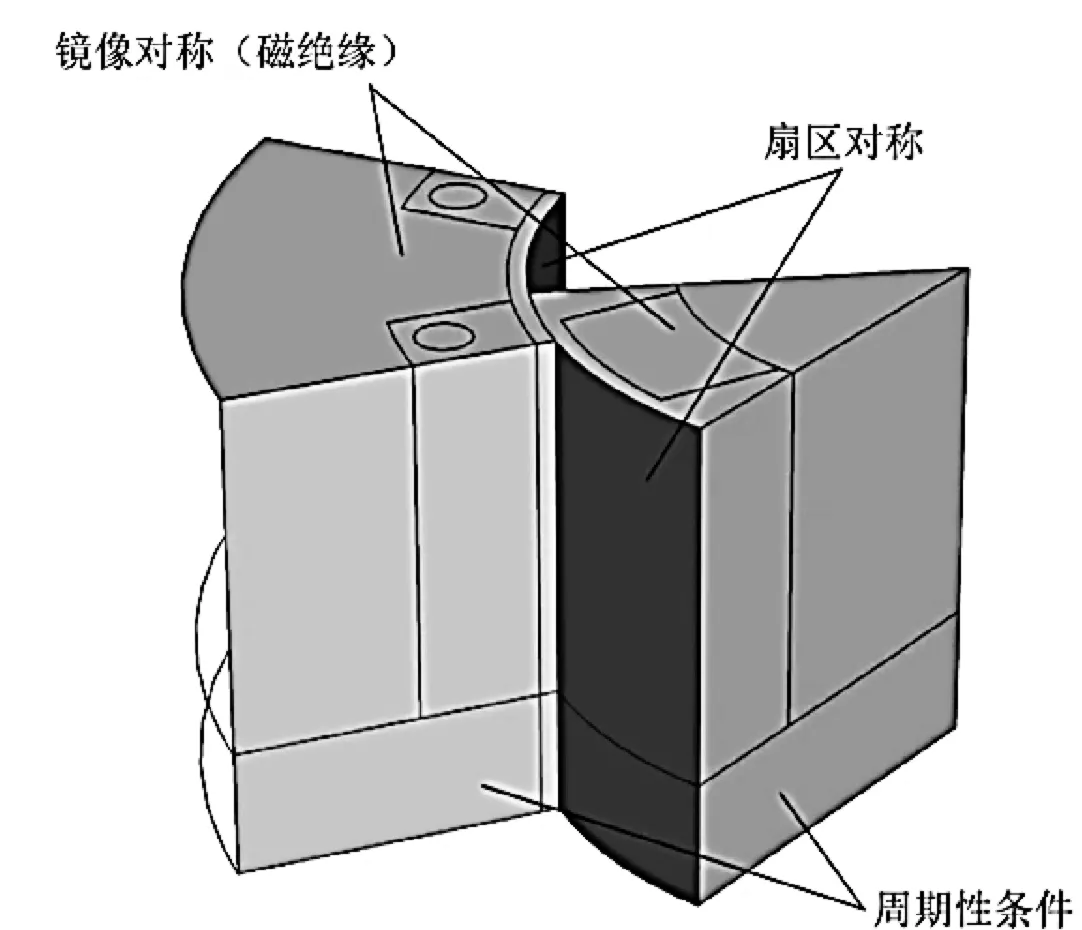
图2 简化模型图

对于简化后的模型，对其进行设置，简化模型的扇区对称的两个侧面使用周期性边界条件，由于模型输入时相邻扇区中的永磁体剩余磁通密度在相邻扇区由正变负，因此周期类型设置为反周期性。对于转子与定子的接触边界创建几何序列中转子域和定子域的联合体如图3所示，并在其上也应用扇区对称条件，周期类型选择反周期性，而默认的磁绝缘特征施加了使磁场的法向分量在中面处为零。

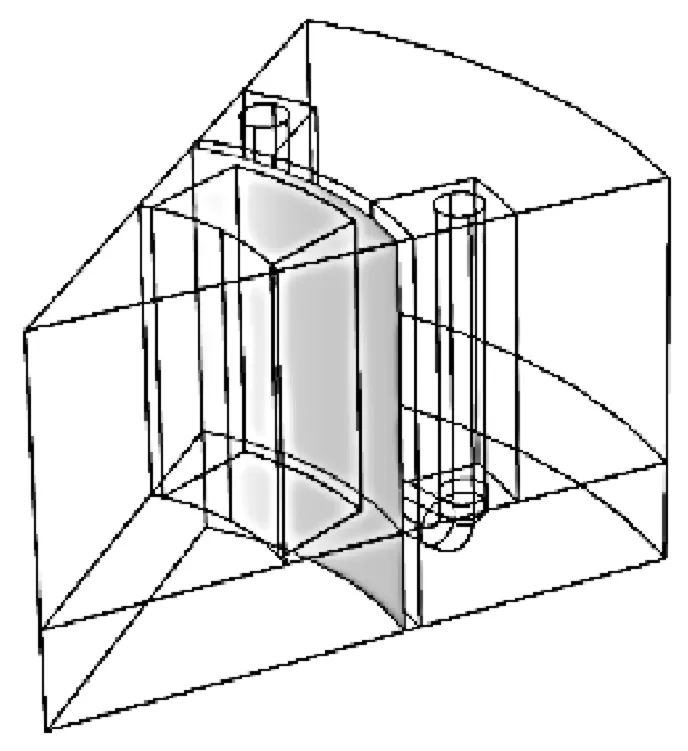
图3 联合体的设置图

1.3 模型的搭建

简化后的模型由两大部分组成，转子和定子区域定子线圈的形状不规则，不属于“线性”或“圆形”这一类。可以采用线圈几何分析步骤计算线圈的方向。定子线圈也受到对称切割的影响。所模拟的线圈长度是实际长度的1/16，其中1/8扇形对称和镜面对称。在模拟此类机械时，从两个转子和定子间的空气间隙处将几何部分切割成两部分，这样就形成了两个不同区域的独立联合体如图4－图5所示。形成装配用于最终的几何定型，在定义下自动创建一致对，定子端部绕组的周围会添加空气域来捕捉弥散场如图6所示。之后，对几何实体进行定义，方便在物理场接口、网格剖分、求解器的设置和后处理。这里我们定义定子线圈、永磁体、旋转域、稳态域和周期性边界条件中的转子和定子。

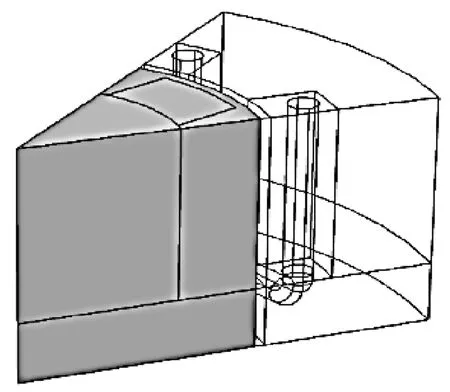
图4 几何序列中的转子域图

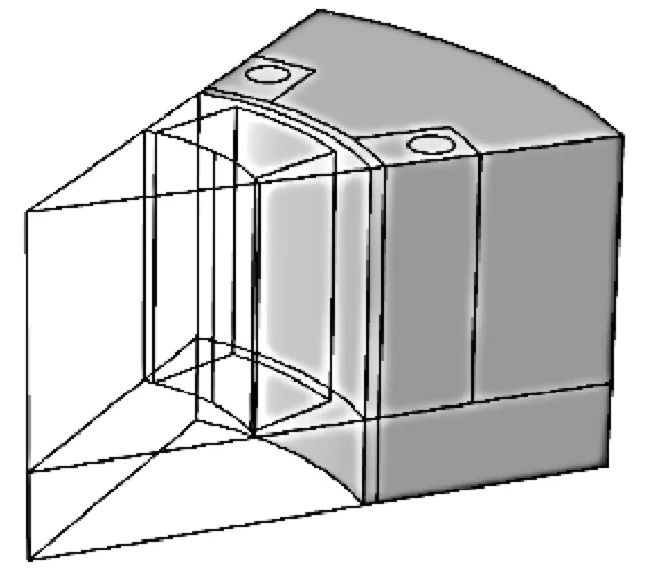
图5 几何序列中的定子域图

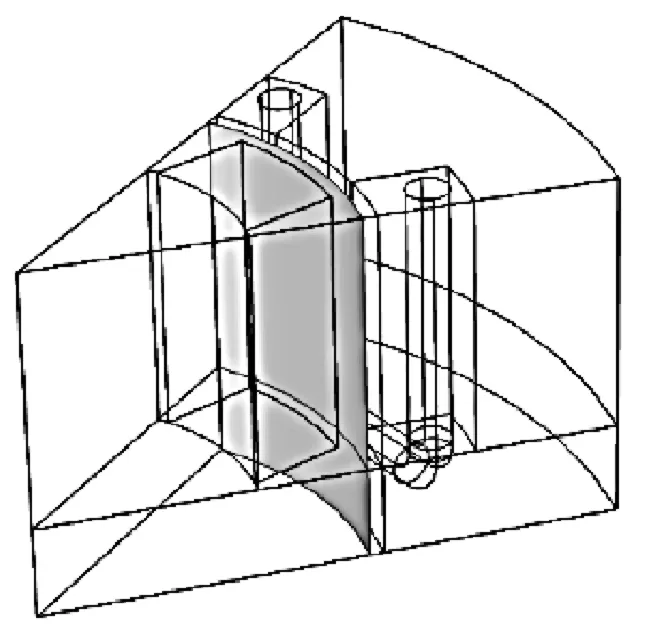
图6 分离转子域和定子域的一致对设计图

2 静态结构分析

将已简化的模型导入到仿真软件中，以转子的中心建立坐标系，将定子固定支撑，对转子的尖端施加一个力模拟磁场对转子的作用力，再将转子的转速设置为1 000转，求解中添加应力等效、总变形与安全系数等，仿真得到定子的变形量为3*10-5，安全系数为7.89，如图7所示。

3 旋转机械，磁接口

3.1 区域的设置

仿真时通过旋转机械，磁接口的混合公式求解功能，用以求解非导电区域的磁矢势A和磁标势Vm。由于在采用扇区对称的模型中为了得到更精准的磁通量守恒，且标量公式相比较于矢量公式自由度也减少了，故对于磁通量守恒特征求解使用标量公式，对于安培定律特征的求解使用矢量公式。在扇区对称模型中使用周期性条件时，模型几何中的拓补区域也必须满足磁标势的条件。

此次仿真中使用磁矢势（MVP）和磁标势（MSP）两种方式来求解MAXWELL方程，定子一侧的定子线圈、定子铁芯和空气域是用 MVP（磁矢势）模拟的。转子的转子铁芯、永磁体和空气域以及定子的一部分空气域是用 MSP（磁标势）模拟的，如图8所示。

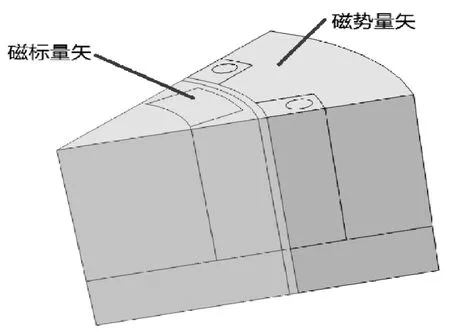
图8 MSP和MVP区域图

3.2 利用磁标势模拟空气域

首先，添加第一个磁通量守恒特征，将其应用到转子侧的空气域以及定子侧中一致对旁的空气域。将本构关系设置为具有相对磁导率的线性材料，并引用材料节点中的材料空气并利用 MSP 模拟空气域。

3.3 模拟转子中的线性或非线性磁性材料和永磁体

添加另一个磁通量守恒特征指派给转子铁芯。本构关系设置为磁导率有限的线性材料，或者利用B-H曲线选项将其改为非线性材料。B-H 曲线通常在材料节点下定义。并且非线性饱和曲线可以通过外部材料特征在外部定义，此特征位于全局定义下的材料节点中。永磁体的模拟同样使用使用磁通量守特征。本构关系设成剩余磁通密度或磁化。柱坐标系用于在径向指派磁化。

3.4 定子线圈的模拟

利用多匝线圈特征模拟定子线圈，通过设置线圈测量绕组中的开路电压，此时电流为零。线圈长度倍增因子中为 16，便能获得线圈总长度，这个参数位于多匝线圈，线圈面积倍增因子为1。之后通过设定指定定子线圈两端的输入和输出的边界条件。

3.5 模拟定子铁芯区域

模拟定子铁芯区域，向模型添加第二个安培定律特征。本构关系通过相对磁导率设置为磁导率有限的线性材料，或通过H-B 曲线选项改为非线性磁性饱和曲线。H-B曲线与转子铁芯相似，在材料节点下定义。不过，如果定子和转子的材料不同，则要在材料节点下添加两种不同的非线性材料。本次对定子铁芯设置的相对磁导率为10 s/m。

3.6 周期性边界条件的设定

将周期性边界应用到几何并分割成多个扇区产生的边界上。如果所有扇区完全相同 ，则选择连续性。若扇区的几何相同，但相邻扇区的激励（即永磁体或电流）方向发生改变，则选择反周期性。后一种情况适用于交流发电机示例，因为相邻扇区的磁化是交变的。此时使用两种不同的周期性条件特征，定子和转子各使用一个如图9所示，以确保能正确检测到周期性边界。

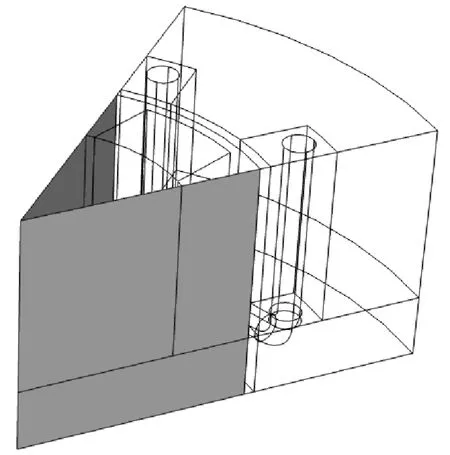
图9 转子区域图

在扇区对称，此成对条件应用到转子和定子的连接对中。在设置窗口中，扇区数和周期性的类型与周期性条件中的类型一致。在转子和定子重叠的区域，扇区对称与连续对特征的效果相似，并将循环对称条件应用于非重叠区域。

3.7 反周期性条件的扇区对称设置

要使求解器收敛，MSP磁标势的解必须唯一。为此，向MSP 区域中的某一点添加零磁标量势。如果恰好定子和转子各有一个，存在两个不同的 MSP区域，则必须向每个区域应用单点约束。这样就存在零磁标势MSP定义对点的约束如图10所示。

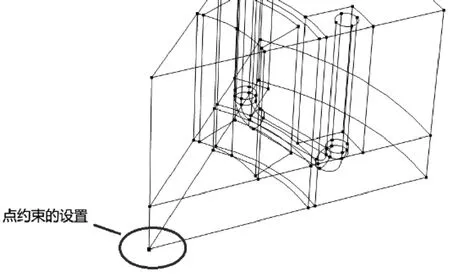
图10 点约束图

4 网格部分

首先，将自由三角形网格或映射网格应用于源边界。然后，使用复制面（副本）特征将相同的网格复制到目标边界上。如图11所示。尽可能地使用扫掠网格或映射网格，这样可以大幅度减少网格单元的数量。先将自由三角形网格应用于多匝线圈特征的一端，然后将扫掠网格应用到整个线圈区域。类似地，扫掠网格也用于定子和转子之间的空气域。最终的网格如图12所示。

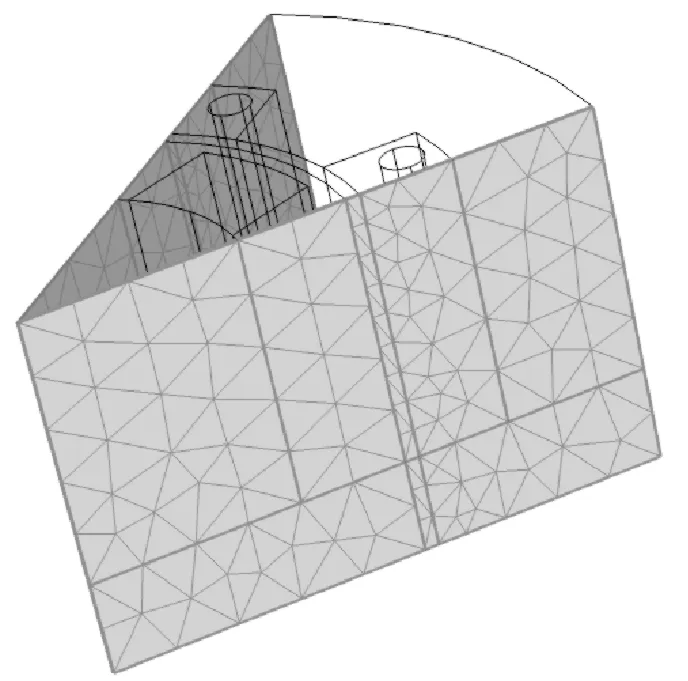
图11 周期性条件下源边界和目标边界的复制面（副本）特征设置

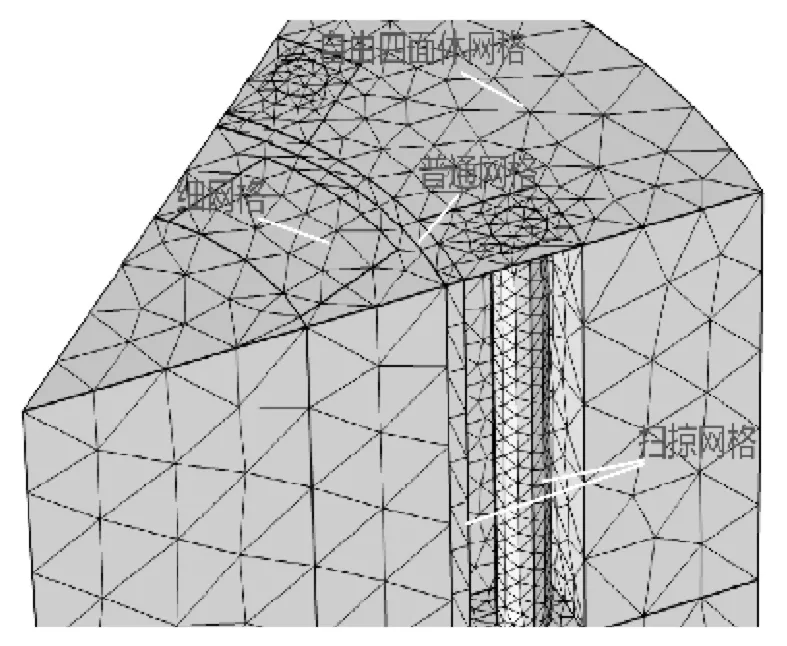
图12 发电机模型最终网格图

5 求解结果

磁通密度和线圈电压的扇区图如图13所示。绘制的解位于转子移动的空间坐标系中。

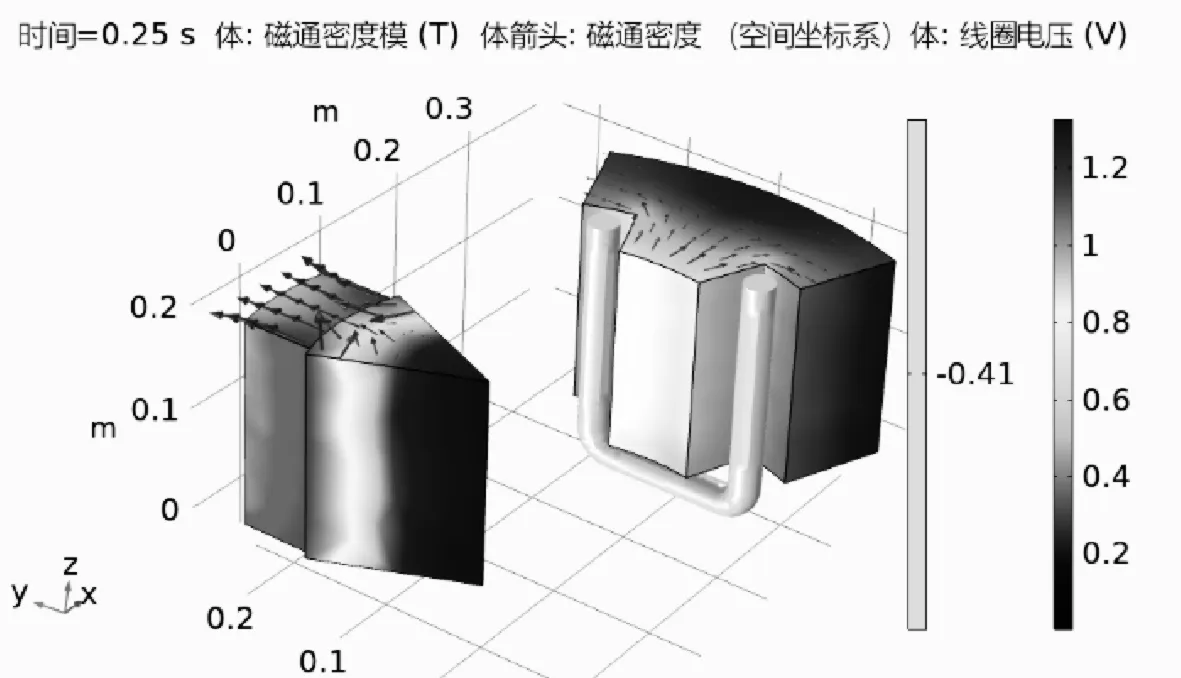
图13 磁通密度的扇区图

此时，可以使用三维扇区和三维镜像对数据集进行重新搭建，并对数据集进行旋转和镜像操作后，会得到新的解。在三维扇区数据集中选择旋转时反相，并在创建毗邻扇区时将解由正值改为负值，如图14所示。

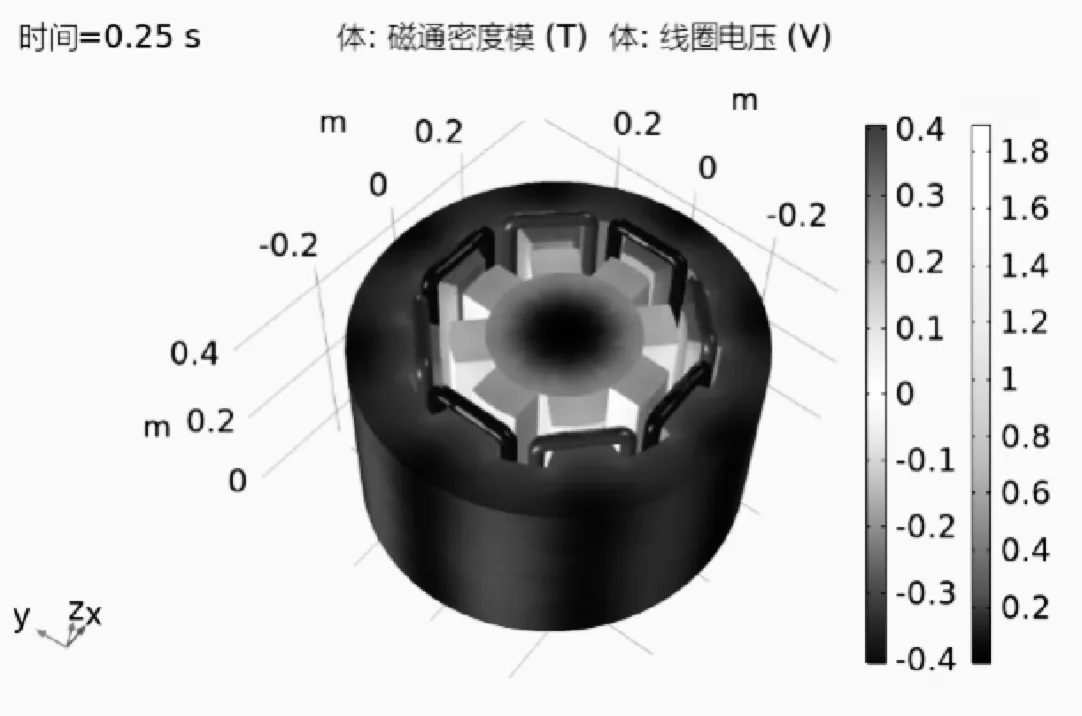
图14 重建后完整几何结构中的磁通密度和全局线圈电压图

最后，得出感应线圈的电压随时间的变化的情况，如图15所示。

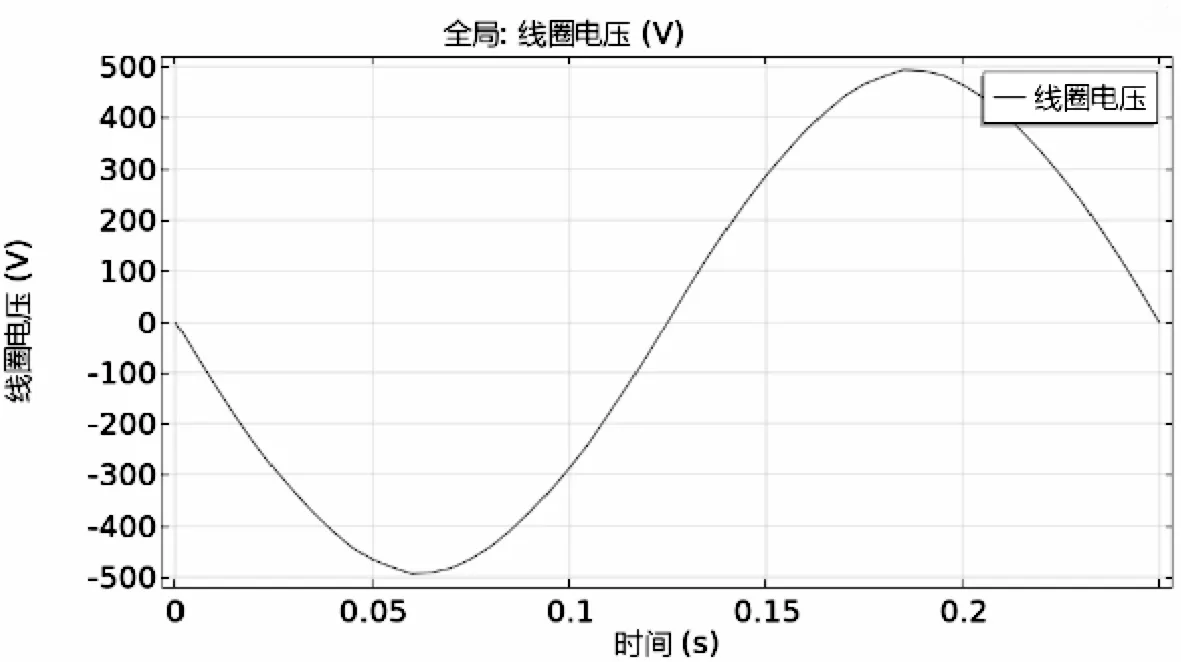
图15 整个线圈中感应电时间变化的情况图

综上，本次仿真通过模型的搭建、简化，到之后的静态结构分析，交流电机中各区域的划分和旋转机械磁接口的设置，最后进行网格剖分，求解器设置和得出最终感应线圈中电压随时间的变化曲线。