基于Matlab的悬置系统固有频率及其解耦率分析

秦 宬，徐兆峰，龚佳强

（比亚迪汽车工业有限公司，广东 深圳 518118）

前言

本文通过动力学建模和振动理论分析，借助Matlab进行了电动总成悬置系统的固有频率及其解耦计算程序的开发，同时与adams分析软件对比计算结果来验证程序开发的正确性，从而进行全面地推广运用。

1 悬置系统的隔振机理

根据振动理论分析，由强制振动施加到自由振动的振波上，开始时运动情况比较复杂，经过一定时间后，自振波的振幅将变得很小而可忽略，而只留下强制振动的成分，但这种受迫振动的振幅与频率比有很大的关系（频率比就是强制振动的频率与自振频率之比）。如果将强制振动的振幅称之为输入振幅，将受迫振动的振幅称为输出振幅，则输出振幅与输入振幅之比可称为“振动传递率”，显然，振动传递率大于1表示振动被放大，而振动传递率小于1则表示振动被减小。

频率比与振动传递率之间的关系可用下式表达：

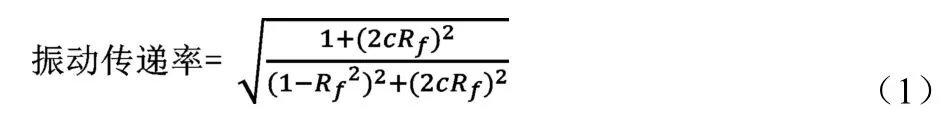
Rf——频率比（强制振动频率/自振频率）；

c——阻尼比。

将式（1）运用Matlab可以作出不同阻尼下的频率比与振动传递率关系曲线，如图1所示。从图中可以看出频率比Rf小于1时，振动被放大。频率比Rf等于1时，振动传递率最大（共振）。频率比Rf继续增大，振动传递率就逐渐下降，当频率比Rf等于时，振动传递率等于1，因而产生隔振效果，且频率比Rf越大，隔振效果越好，但频率比大于5以后，隔振效果的提高就不明显，因此实际的设计过程中频率比Rf一般取2~5之间。

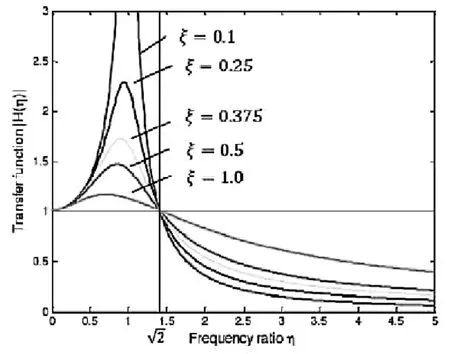
图1 不同阻尼下的幅频响应曲线

2 电动商用车悬置系统设计原则

对于一个电动总成悬置系统，有6阶刚体模态，对应6个固有频率，它们分别对应x、y、z方向的平移和绕这三个方向的旋转。通常，电动总成悬置系统的六个固有振型在多个自由度方向上是耦合的，在某个自由度方向上进行激振就会产生其它自由度方向上的耦合振动，这样使得共振频率的范围大大加宽。因此，电动商用车在悬置系统的设计过程中不仅需要考虑避开来自路面、电机的激振，同时还要避免振动耦合的情况。

2.1 悬置系统固有频率设计原则

悬置系统固有频率的设计原则需要综合考虑乘客对各个方向振动的敏感程度，同时还避开来自路面、电动总成的激励，其主要有以下几点要素：

（1）乘客对水平方向振动的敏感区一般为1～2 Hz，垂直方向振动的敏感区一般为4～8 Hz[1]；

（2）道路随机激励经过悬架衰减、过滤后的频率一般不超过2.5 Hz；

（3）当电机处于高速运转时，即便转子的不均匀的质量不是很大，也会产生较大的离心力，取电机峰值转速nmax，其激励频率为（nmax/60）Hz[2]；

（4）为避免动力总成的位移过大过而造成空间干涉，悬置系统的刚度不应过小，与刚度成正比关系的悬置系统固有频率应不小于5 Hz；

（5）为防止悬置系统振动耦合，各阶固有频率间隔应不小于1 Hz。

结合前面所述的隔振机理，悬置系统要达到良好的隔振效果频率比一般需要取到2～5之间，本文取2作为要求，因此，悬置系统固有频率应处于6 Hz～（nmax/120） Hz 之间，其中Z向作为乘客的敏感振动的固有频率应处于9 Hz～（nmax/120）Hz，其他方向的固有频率处于6 Hz～（nmax/ 120） Hz，这样就可以很好的避开来自路面、电动总成的激励，同时还可以带给乘客舒适的乘坐环境。

2.2 悬置系统解耦率设计原则

对于电动商用车，Z向作为主要的振动方向，其解耦率应不小于90%，其他各个方向的解耦率应不小于80%。刚度和侧倾刚度，在转向时为整车提供一定的侧向支撑，减小侧倾梯度。

3 悬置系统动力学模型

如图2所示为某车型四点悬置的布置，将电动总成视为一个具有质量（m）、惯量（Jxx Jyy Jzz Jxy Jxz Jyz）的刚体，其在整车坐标系下的位置为电动总成质心坐标（X0，Y0，Z0），其质量与惯量组成的电动总成惯性矩阵表示为：

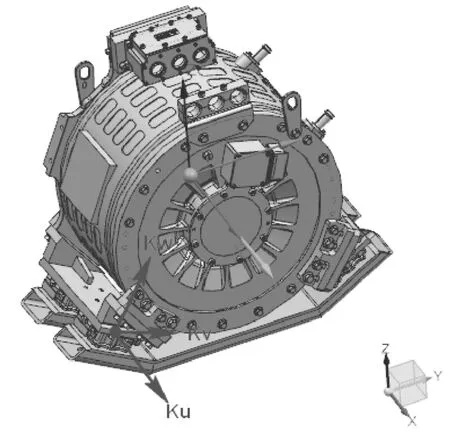
图2 某车型悬置布置

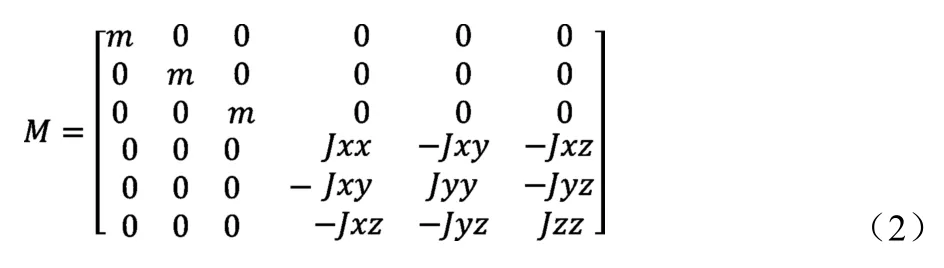
将悬置视为具有3 个互相垂直主轴刚度（Ku，Kv，Kw）的弹簧，各悬置的刚度矩阵表示为：

各悬置在整车坐标系下的位置为（Xi，Yi，Zi），悬置主轴在整车坐标系下的方向用角度矩阵表示为：

由于悬置系统的频率及解耦分析都是相对于电动总成质心来求解的因此第i个悬置刚度相对电动总成质心坐标变换矩阵Bi和角度变换矩阵Ti为：

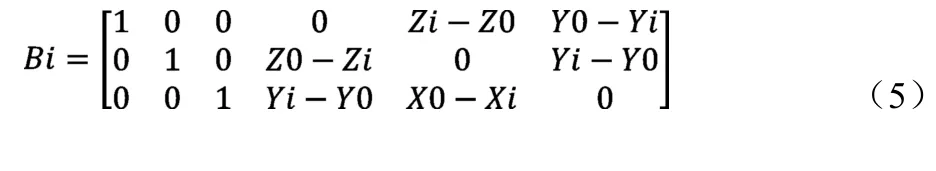
4 Matlab程序开发

4.1 设计参数输入界面

如图3所示，通过GUI界面设计，可以将式（2）～（5）中涉及的所有设计参数归纳作为前端输入，其操作相比adams更为简单，同时也可以保证数据输入的准确性。

图3 悬置的解耦计算界面

4.2 计算程序编辑

在底层m文件中通过eig语句实现特征值即悬置系统固有频率的求解，如图4所示。通过伴随矩阵求解第i阶主振型，进一步使用matlab中循环嵌套语句实现解耦率的计算，如图5所示。

图4 悬置系统的固有频率计算语句

图5 悬置系统的主振型计算语句

4.3 程序验证

讲某车型实际参数通过GUI界面输入至开发程序中，计算得到的悬置系统固有频率及解耦率如图6所示，其计算结果与Adams（图7所示）计算结果基本一致，进一步验证了本程序的正确性。

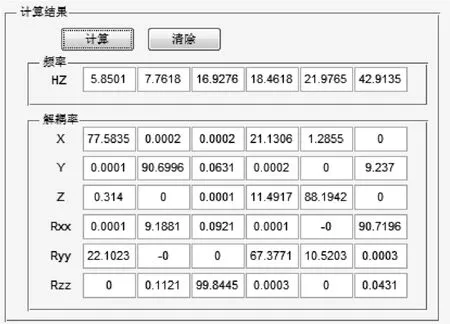
图6 某车型悬置系统解耦计算（开发程序）

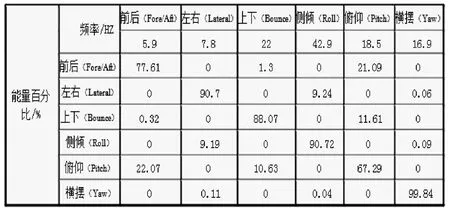
图7 某车型悬置系统解耦计算（Adams）

5 结论

本文主要基于悬置系统的隔振机理并定义了电动商用车悬置系统的NVH特性要求及其设计原则。

通过建立悬置系统动力学模型求解系统固有频率及解耦率，并借助matlab开发出操作简单、实用性高的程序进行计算，通过与adams软件的计算结果对比验证程序的正确性，可进一步推广使用。

本程序操作界面简单、准确性高，进一步提高设计工作效率，可为后续的正向优化设计提供帮助。