飞行器翼面协同优化中的气动代理模型研究

席 睿，李 冰，贾宏光

（1.华北水利水电大学 机械学院，河南 郑州 450011；2.中国科学院长春光学精密机械与物理研究所， 吉林 长春 130033；3.长光卫星技术有限公司，吉林 长春 130033）

引言

在飞行器设计中，其尾翼的设计的水平对其性能有重要影响。对此类翼面结构的设计涉及气动、结构、气动弹性多个领域，传统设计只在单一的气动或结构学科内独立优化而忽略气动弹性作用对性能参数的影响，或只考虑简单的静气动弹性影响而不考虑其动态气动弹性现象的作用。忽略这些弹性变形会影响翼面优化设计结果的准确性，使设计的翼面在实际飞行中很难达到预期的性能。因此，需要对其进行多个学科的分析以研究其协同效应并借助先进的优化策略和有效算法才能实现综合性能的最优化。近年来在飞行器的研发模式中，多学科优化算法（Multidisciplinary Design Optimiza- tion, MDO）和快速迭代成为主要研究方向[1]。

目前，国内外研究人员在航天领域的产品设计中，就多学科优化理论的应用进行了广泛的研究，多学科设计优化（MDO）的研究起源于20世纪70年代，在20世纪80年代发展为一个单独的研究领域。

到了20世纪90年代，MDO的研究已在世界范围获得了关注，不仅在理论研究上取得更多进展，更是在工程上得到了实际应用。比较典型的案例如Rockdyne公司的计划用于X-33的塞式喷管发动机的设计，该设计以总升重比为目标函数，采用耦合计算流体力学的模型、结构有限元模型、计算热力学模型等多学科的MDO模型，其结果不仅提高了设计质量，还大大减少了设计时间。另一个计划是高速民用飞机（HSCT）的设计，该研究利用分布式网络和并行设计方法缩短了设计周期、获得了更佳方案。国内对这方面的研究是20世纪90年代中期开始的，通过向国外学习也取得了一些进展，如文献[2-4]研究了多学科设计算法在飞行器设计中的应用。文献[5]提出了混合多目标粒子群算法在飞行器气动布局设计中的应用。文献[6]对航天器性能样机提出了一种气动一体化多目标优化方法。

飞行器的气动计算对整体方案设计影响较大，在传统设计中，多采用基于有势能、小扰动的工程算法，适用范围小且需要后期修正，难以引入多学科优化框架。现今对气动特性计算主要依靠计算流体力学（CFD）仿真计算和风洞实验，这种高精度计算量很大，无法满足设计中快速分析的需求。

目前在飞行器设计领域中针对多学科优化和气动外形优化的问题多采用利用代理模型技术利用实验设计法（DOE）获得样本并选择近似方法来拟合气动特性对外形参数的响应，以达到避免复杂数值计算、缩短设计周期的目的。近年来代理模型在航空、汽车、船舶的设计和优化中都得到了广泛的应用。

本文按照图1的设计流程针对飞行器翼面的外形，对气动特性参数进行多种类型代理模型构建，探索不同近似方法的精度和计算成本差别，选取最合适的近似算法参与翼面的气动－结构协同优化。

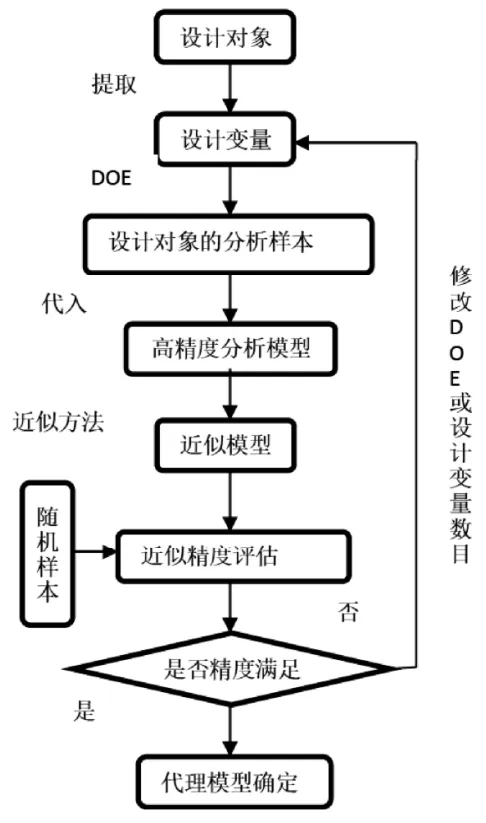
图1 代理模型构建流程图

1 设计空间

飞行器的飞行环境需要跨声速飞行，应采用大后掠翼，同时设计状态属于超声速，应采用小展弦比的薄弹翼，六角翼型，其结构如图2所示，其几何参数含义见表1。

图2 飞行器翼面几何参数示意图

表1 翼面几何参数

翼面的建模几何参数只适合对翼面进行三维建模，对于描述一个固定的翼面形状，往往需要将其换算为一系列无量纲参数即优化所涉及的设计变量X={λ, χ,b1,b2,c’root, k}，其中λ代表展弦比、χ代表前缘后掠角、b1代表翼前缘特征、b2代表后缘特征、c’root代表翼根相对厚度和k代表翼梢收缩比。

参考飞行器设计工程经验[7]确定了设计变量的取值范围，如表2所示。

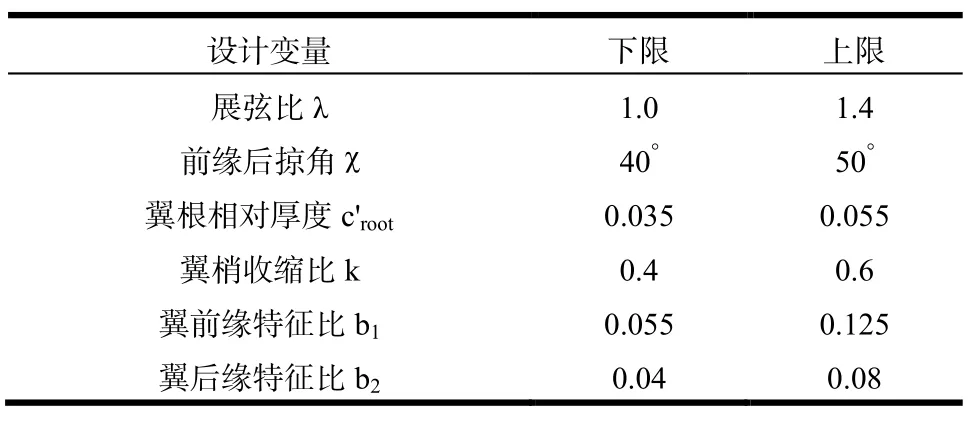
表2 翼面设计变量区间

2 试验设计

试验设计技术（Design of Experiment, DOE）是多学科设计优化中代理模型的取样策略。试验设计中，系统的输入变量被称为因素（Factor），其在样本点处的值被称为水平（Level），样本点对应对的输出值被称为响应（Responce）。

2.1 全析因设计

全析因设计（Full factorial）是指在一次完全试验中，系统的所有因素的所有水平可能的组合都要被研究到的一种试验设计方法[8]。

假设系统输入变量也即因素的个数为nv，每个因素对应的水平数为ni（i =1,…,n），则对系统进行全析因试验所需的试验次数为：

全析因试验能够分析因素对系统影响的大小和分析因素间的交互作用，但当系统的因素和水平比较多时，根据上式计算所得的试验次数，即样本点个数会将会是一个很大的数字，所以除了低维低水平的问题，全析因试验很不适用。

2.2 中心复合设计

中心复合设计（Central Composite Design, CCD）[9]是一种针对二次多项式响应面模型进行分批实验的一种试验设计方法。该方法先挑出每个因素最大和最小的两个水平值利用正交表Ln（2nv）安排n次试验，试验结束后在中心点做n0次重复试验，最后在每个因素的坐标轴上，取臂长为α的两个对称点作为样本点，臂长的确定按下式：

若因素的个数为nv，三次试验总样本点数N=n+n0+2nv，N个点分布在以中心点为球心的两个同心球上。

2.3 拉丁方设计

拉丁方（Latin Hypercube）[10]，它是一种分层抽样法，将每个因素的设计空间均匀分成n份构成矩阵，按水平数随机组合成下标，在设计空间矩阵上取样本点，每个因素水平只可用一次。试验点在设计空间内均匀分布，且是随机的，每次采样的结果都不相同。这种设计均匀性比较好，适合因素数目较多的情况。

2.4 正交设计

正交试验设计（Orthogonal design）也叫Taguchi设计，是应用范围最广的试验设计方法之一，由日本学者田口玄一于20世纪40年代后期首次应用而得名。这种试验设计方法按照一种己经拟定好地满足正交试验条件的表格来安排试验。表格称为正交表（Orthogonal array），表示为LA（Pn），其中L代表正交表；下标A表示表中横行个数，即总共试验次数；P为因素的水平数，n是因素的个数。当遇到各因素水平数不等的试验时，可使用不等水平正交表或采用拟水平法。正交表可从试验设计参考书中获得[11]。正交设计是多因子试验中最重要的一种设计方法，设计变量最好不多于10个。

考虑到本文高精度模型的计算代价比较高，应尽量减少分析的次数以提高设计效率，相比于全因子设计和中心复合设计，正交设计计算量较小，相比于均匀设计和拉丁方设计，正交设计精度较高[12-13]。鉴于此，本文选择用正交设计技术来生成试验点集合。对设计变量的水平数设置越多，样本点数目也就跟着增加，这样可以提高近似的精度。但考虑到相应的计算量过大，对每个设计变量取5水平。

设计变量在设计空间上水平数的数据如表3所示。

表3 翼面设计变量水平数和水平值

取样即为一组6因素5水平的试验，可使用L25（56）正交表来安排试验，即需要进行25次不同输入的气动特性仿真，输入安排如表1所示。

3 数值分析响应值提取

本文对25组不同翼面形状的飞行器进行了基于CFD/ CSD紧耦合方式的高精度学科分析。对分析结果提取翼面优化所需的参数即升力系数CL、阻力系数CD、结构最大应力σmax、翼梢变形δmax、弹翼重量Weight作为响应值。

考虑到气动弹性现象，与进行了气动弹性仿真后得到数值相比，后者更符合风洞实验值[14]。所以响应值应提取考虑了弹翼气动弹性现象的仿真结果。

4 代理模型近似方案确定

近似技术也称代理模型方法，是代理模型技术的核心，其本质是利用已知样本点以数学手段生成能够反映设计变量与响应值之间映射关系的数学模型。多项式响应面（Polyno- mial Response Surface Method, PRSM）、径向基函数神经网络（Radial Basis Squares Method, RBF-ANN）和Kriging模型（Kriging Model, KM）是多学科设计优化中常用的代理模型方法。

4.1 多项式响应面

响应面法是一种用简单的代数函数来表示高精度模型分析信息的近似方法。工程中最常用的二阶响应面模型的数学表达式如下式所示：

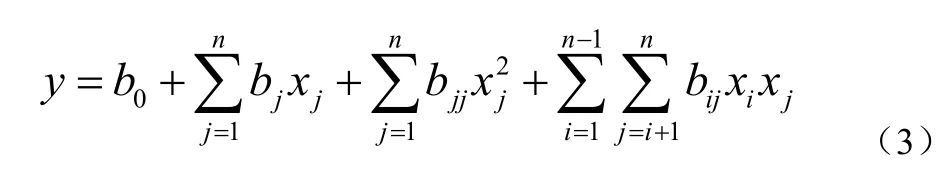
式中n为设计变量的维数；xi,xj为设计变量；待定系数b0，bj，bjj，bij可由最小二乘法确定。为了更高的精度可建立阶数更高的响应面模型，但响应面模型的阶数越高，所需的样本点即高精度模型的分析次数越多。如以二阶响应面模型为例，需要不低于（n+1）（n+2）/2个高精度模型的分析信息。

4.2 RBF神经网络

人工神经网络是一种模拟生物大脑结构的信息处理系统，除了可以用来进行函数逼近还可以进行最近相邻模型分类、概率密度估计等计算，在多个领域均有应用。

神经网络的结构由输入层、隐层和输出层三层处理单元组成。信号输入和输出的单元层分别为输入层和输出层，输入层和输出层中间的单元层称为中间层或隐层。

层中的数据处理单元称神经元。在神经元中将输入激励转化为输出响应的数学表达式称为传递函数。

神经网络各神经元通过权值连接，在各层类型决定后，通过已知样本点的设计量及状态量数据来调整确定权值即训练网络。训练结束后，网络的输出即由输入数据和各单元相连的各输入量的权值来决定，此时即可用来模拟原有样本和响应值的映射关系。

BP神经网络和RBF神经网络是最常被用作代理模型的两种模型，二者都是前馈网络。相比之下后者的结构更为简单，网络的训练过程更为快捷，并且在函数逼近和模式识别方面的表现也更为优秀。所以对非线性函数的逼近，选用RBF神经网络较为合适。

图3所示的是一个典型的r维输入的单隐层RBF网络。其中‖dist‖表示求输入矢量p和权值矢量w的距离；b1,b2为阈值；n为隐层输入：

图3 r维输入的单隐层RBF网络

其中LW是隐层到输出层的权值。

Jin等人[15]的研究表明RBF神经网络的近似精度和效率都不错，适合在MDO中应用。

4.3 Kriging方法

Kriging模型是Danie Krige于20世纪50年代提出的一种估计方差最小的无偏估计模型，由全局模型和局部偏差叠加而成。该模型早期主要应用在地质领域，到现在已经成为MDO中比较有代表性的一种代理模型近似方法[16]，其具体模型为：

其中近似项g（x）是设计空间内的全局模拟，g（x）可以看作一个常数β，β值可由已知响应值进行估计。估计项Z（x）期望为0，方差为σ2，协方差不为零的随机函数，表示全局模拟的插值，是全局模拟基础上的局部偏差。上式可变为：

式中R是相关矩阵，矩阵为对角线元素为1的对称矩阵；R是相关函数；ns为样本点个数。R选择高斯函数，可以表示为：

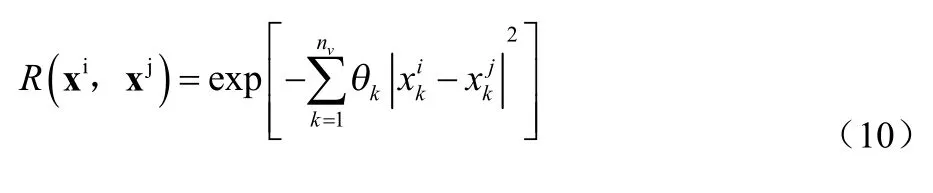
式中nv是设计变量个数，θk为未知相关参数向量，可取为常数以简化运算。

根据Kriging理论，未知点x处的响应值y的估计值y′可表示为：

式中y是样本点响应值组成的ns维列向量；g为长度为n的单位列向量；r（x）是未知向量x与样本输入数据之间的关系向量：

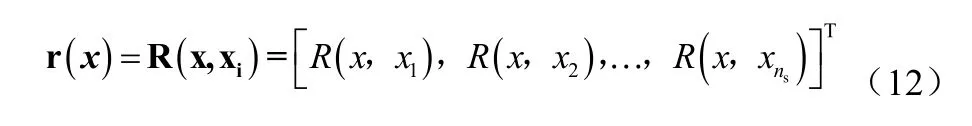
相关参数向量θk取为常数θ，可由极大似然估计变为一维优化问题：

4.4 代理模型综合评估标准

为了判断代理模型是否可以代替原有分析模型，需要一定的评估检验标准，包括精度评估、效率评估和实现难度评估。

考虑到Kriging和RBF这样的近似方法具有插值特性。所以需要在构造的样本点以外重新选取另外一批样本点作为测试样本点来参与对精度的评价。本文采用均方根误差（Root Mean Square Error, RMSE）和复相关系数（R Squared Coef- ficient, R2）两个标准来检验该模型的预测值对真实值的代理精度：

其中y和yreg分别是设计空间内每个样本点的真实响应值和模型预测值；为所有样本点真实响应值的平均值；Ngrid是样本点的个数。RMSE值越接近于0则代理模型精度越高。复相关系数R2的取值越接近于1则近似精度越高。

效率评估考虑的是代理模型的计算效率，评价的指标是构造代理模型所需要的成本与使用代理模型预测新的设计点响应值所需的成本。这个成本包括计算时间计算所需的PC机内存等，一般用计算时间来评价。

代理模型的实现难度指的是在软件上的功能实现。目前工程上最常用的实现手段是基于Matlab环境的各种函数工具箱来实现自行开发。也有一些优化软件自身带有一套近似模型模块，可以省去编程而方便工程人员使用。但是由于程序代码固定，当需要对程序进行修改时往往比较困难。一般来说，近似方法的原理越复杂，软件开发就越困难。但是为了获得较高的精度，有时必须对模型反复修改使之复杂性增加。

本文以设计变量集合X={λ，χ，b1，b2，c’root，k}为输入，分别以响应值集合Y1={CL}，Y2={CD}，Y3={σmax}, Y4={δmax}，Y5={Weight}为输出，采用多项式响应面、RBF神经网络和Kriging方法为近似方法各自创建了近似模型。在设计空间内随机生成五个测试样本点，以均方根误差RMSE和复相关系数R2为代理模型精度评价标准。

用这三种模型的近似精度校验结果和时间统计分别如表4和表5所示：

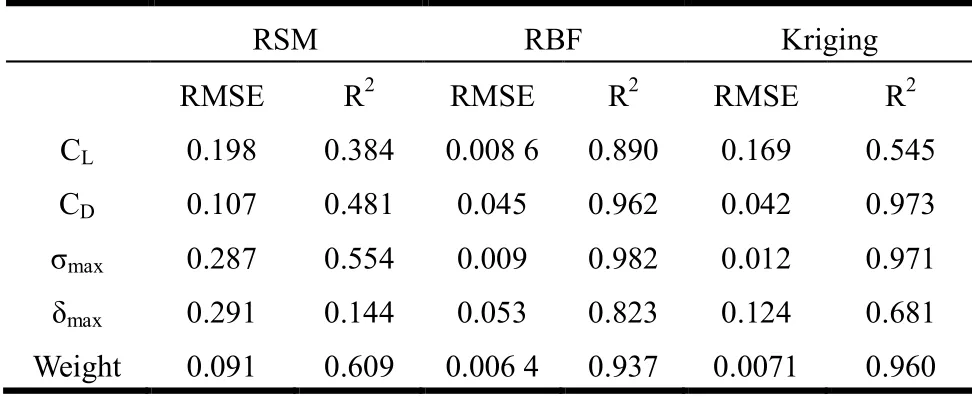
表4 近似精度校验结果

表5 代理模型时间统计

5 结论

从表中数据可以看出，多项式响应面得到得近似模型整体效果最差，所有响应的精度都低于其他两种方法，产生这种结果的原因是设计变量维数（即因素数目）有6个，要构建一个6因素的二阶多项式需要至少（6+1）（6+2）/2=28个样本点，而样本点数目只有25个，所以造成只能使用一阶多项式来近似模型，这样显著降低了近似精度。不过由于许多研究以表明多项式响应面法本身不适合高阶非线性问题，所以这种方案对本文翼面优化的代理模型来说是不可取的。

Kriging方法与RBF神经网络相比，对某些数据如CD和Weight的近似效果比较好，但是对CL和δmax的近似精度则较低，RSM的值都高于0.1，R2值也都低于0.7。

RBF神经网络对所有数据的RMSE值均低于0.01，R2值均大于0.8。所以其整体近似精度要更为优秀，具有更好的鲁棒性。

就构造代理模型的时间而言，多项式响应面所用的时间最少，Kriging方法需要的时间最多，这与这三者本身数学模型的复杂度相符合。在主频2.6 GHz，单核的PC机上这三种方法所耗费的预测时间均在1 s以内，而主频2.6 GHz，8核的服务器上对任一个样本点进行高精度仿真的计算时间则在20 h以上。相比而言，使用代理模型大大提高了学科分析的效率。

通过上述研究可以看出，多项式响应面虽然效率最高但精度过低，Kriging方法可以对测试问题取得较好的精度，但是鲁棒性差，而且耗时较多，RBF神经网络各项性能较为平均，综合性能最好。考虑到气动优化时所需要的迭代点很多，而且数据之间关系复杂，本文选用了RBF神经网络作为翼面优化设计的代理模型近似方法。