基于预瞄的汽车自主换道控制

隋官昇，赵 博，杨昌耿，贾永辉

（1.吉林大学 汽车工程学院，吉林 长春 130022；2.中动智轮科技有限公司，广西 柳州 545006； 3.上汽通用五菱汽车股份有限公司，广西 柳州 545007）

引言

换道是最常见的一种驾驶操作，可靠、高效且安全的换道行为可以提高道路通行效率、缓解交通拥堵状况和减少事故发生。随着智慧交通系统和智能车辆技术的深入研究以及雷达传感器等硬件设备的日趋成熟完善，无人驾驶汽车的自主换道系统可以大大降低人为因素造成的风险。

轨迹跟踪就是控制车辆按照预定的轨迹行驶，是当前自动驾驶的研究重点之一，保障了汽车行驶的安全。国内外学者针对轨迹跟踪控制问题提出了许多研究方法，比如PID控制、最优控制、滑模控制、模型预测控制等。PID控制算法简单，且无需搭建模型，但参数需要不断调试，耗费时间长，且鲁棒性差，易受到外界干扰，因此PID算法的应用目前正在减少。最优控制算法可以对跟踪误差模型做线性化处理，极大地简化计算量，并且可以根据系统的要求，通过最优求解得到最优控制输入。模型预测算法（MPC）广泛应用于工业领域，在智能控制领域也得到了实际运用，该算法通过模型预测、滚动优化、反馈矫正等环节实现优化控制，近年来在智能汽车路径跟踪问题上也得到了广泛研究。

孙银健设计了考虑轮胎侧偏角约束的模型预测控制器，并验证在低附着系数路面上以较高车速进行轨迹跟踪的稳定性[1]；王家恩等人以期望横摆角速度作为目标输入，采用滑模控制器跟踪期望轨迹，并验证了控制器具有较好的控制效果[2]；Paolo Falcone等人基于主动转向系统，引入了四轮独立制动，提高了车辆在极端情况下的操纵性和稳定性[3]；李红志等人提出了一种最优预瞄驾驶员模型，设计优化函数来计算预瞄时间，以此对车辆将来的运行状态进行预测[4]。

汽车在行驶过程中遇到障碍物时，有两种躲避方式：一种是制动避障，另一种是换道避障。在交通状况以及路面状况良好的道路上，驾驶员一般采取换道避障的方式来避开障碍物，所以本文主要研究的是汽车换道避障。

1 车辆模型

在车辆动力学模型的建模过程中，模型精度随着自由度的增加而提高，可以更加真实和准确地反应车辆的实际运动状态。但是，模型复杂程度提升也使得控制的难度大大增加。为了简化计算，车辆动力学模型要在能够准确表达的前提下进行。汽车换道时，假定汽车的纵向速度是恒定的，仅考虑侧向和横摆两个自由度的运动，简化后的车辆模型如图1所示。

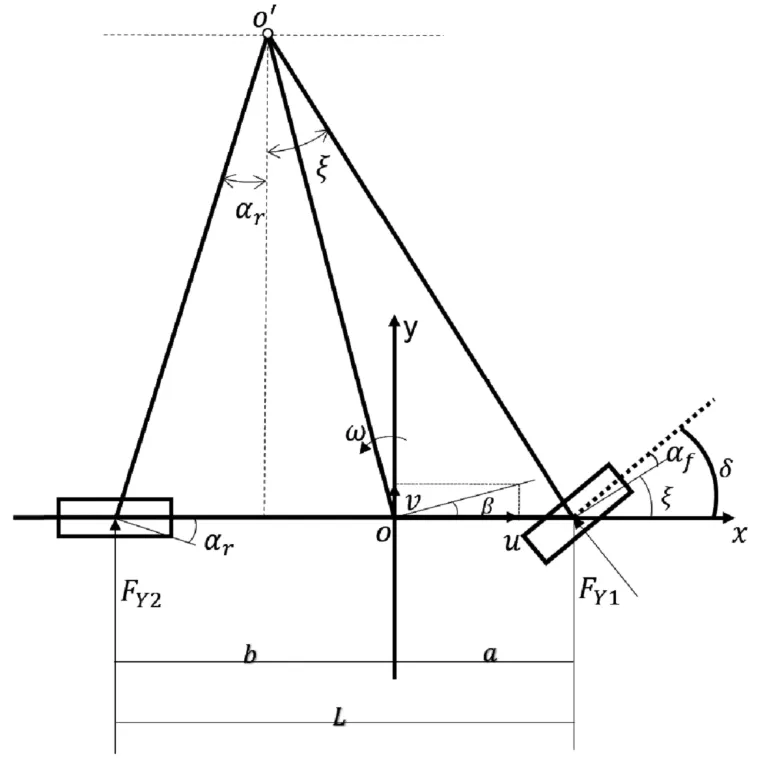
图1 汽车二自由度模型

其中：

ωr——横摆角速度。

单轨车辆模型横向运动和横摆运动的动力学方程为：

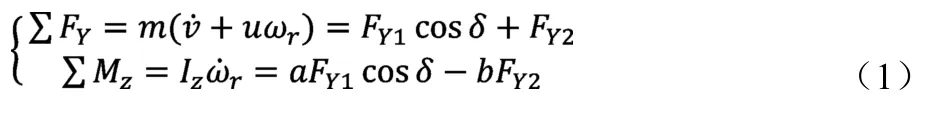
考虑前轮转角很小，因此cosδ≈1，对轮胎模型进行线性化假设，轮胎侧向力满足：

cf、cr为轮胎侧偏刚度。于是式（1）可写成：

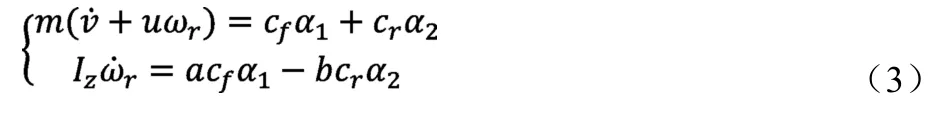
ξ为前轮车速与x轴的夹角，计算公式为：

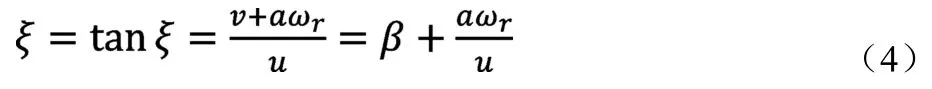
前后轮侧偏角为：

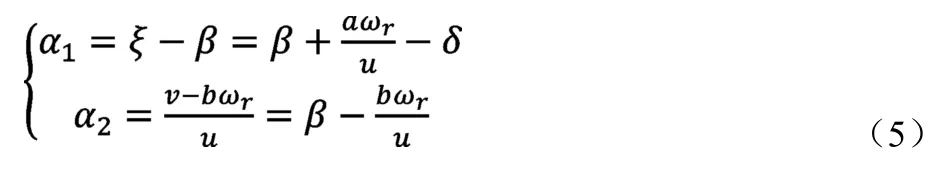
将式（5）带入式（3）中，可得二自由度汽车动力学方程为：

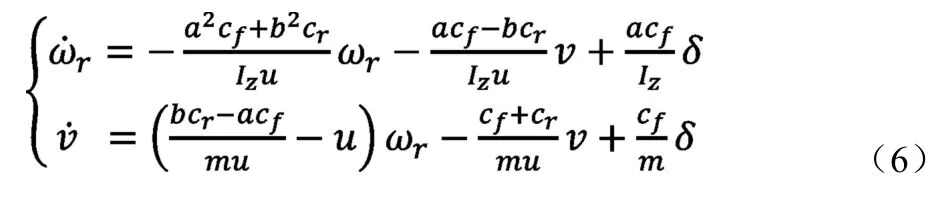
2 换道轨迹规划模型

2.1 纵向安全距离

为了保障行驶的安全，车辆在高速行驶过程中遇到低速行驶的车辆或者障碍物时，要保持合理的安全距离。智能汽车搭载的激光雷达或毫米波雷达等传感器可以很容易获取目标车辆或障碍物的相对距离和速度，一旦车辆和障碍物之间的相对距离小于一定的安全阈值时，汽车的电子控制单元（ECU）就会进行换道轨迹的决策规划，并发出换道避障的指令到底层控制器。

汽车的最小安全换道距离S为：

式中：

vr——汽车与前方低速车辆或障碍物的相对速度；

T——换道时间。

式（7）为了避免碰撞追尾设置安全间隔，仅考虑了最低安全距离，但是车辆与障碍物之间的初始距离不可能为零，这与实际情况有所不符，对此需要添加缓冲距离D。通过查阅相关研究资料和文献，本文缓冲距离设定为3 m，因此换道距离S=Smin+D。

2.2 换道轨迹规划

轨迹规划是车辆运动控制的前提，因此实现车辆换道控制的关键在于轨迹规划。考虑到时间概念，系统依据车辆自身的状态信息和周围道路环境信息，规划合理的车辆行驶轨迹。有别于路径规划，轨迹规划在几何曲线的基础上引入时间因素，考虑了速度、加速度等车辆运动状态参数，并且对车辆行驶的稳定性也有一定的要求。

常用的车辆换道轨迹规划方法主要有：等速偏移换道轨迹、正反梯形换道轨迹、圆弧换道轨迹以及多项式曲线换道轨迹。

（1）等速漂移换道轨迹是一条理想轨迹，由三条线段组成，且假定整个换道过程中车辆的横向加速度为零。但是，实际行驶过程中车辆不可能完全实现直线转向，有悖于车辆实际运动特征，因此车辆无法跟上期望轨迹。

（2）正反梯形换道轨迹考虑车辆侧向加速度的线性变化，通过约束其值的大小，认为换道时侧向加速度的曲线由两个形状相同的正反梯形组成。梯形换道轨迹能够满足曲率连续变化的要求，但模型不够灵活，调整换道过程难度大。

（3）圆弧换道轨迹中间段采用直线，两端用圆弧连接。虽然该模型考虑了对横向加速度的限制，但是存在曲率突变、不连续等问题，无法满足实际换道过程与运动特性。

（4）多项式曲线换道轨迹一般用函数f（t）表示，其结构简单、曲率连续且平滑、计算简便，能够满足换道轨迹的需要，有两种常用的曲线函数：三次多项式轨迹函数和五次多项式轨迹函数。其中，五次及五次以上的多项式函数曲线具有曲率平滑连续和连续三阶可导的优点，在应用过程中能更好地模拟实际曲线，是较为理想的换道轨迹。

本文采用五次多项式来描述车辆的换道轨迹：

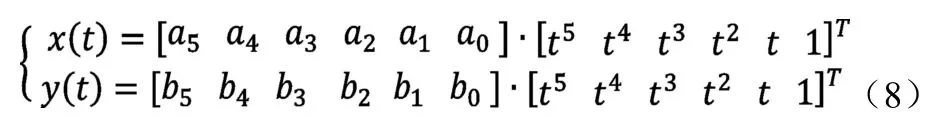
式（8）中，a0～a5，b0～b5表示五次多项式系数，由式（9）（10）确定。

其中：

x0、y0——纵向、横向初始位置；

x1、y1——纵向、横向终点位置；

vx0、vy0——纵向、横向初始车速；

ax0、ay0——纵向、横向初始加速度。

因为汽车在换道过程中的横摆角变化较小，认为车辆的纵向速度是基本不变的，横向车速近似为零，加速度大小也近似为零，即：

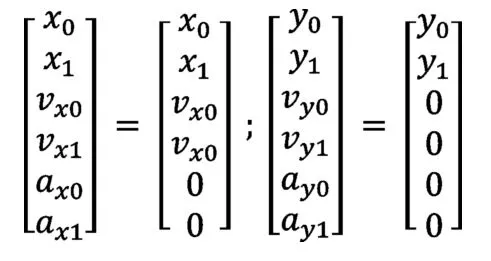
车速为60 km/h、80 km/h、100 km/h的换道轨迹如图2所示：

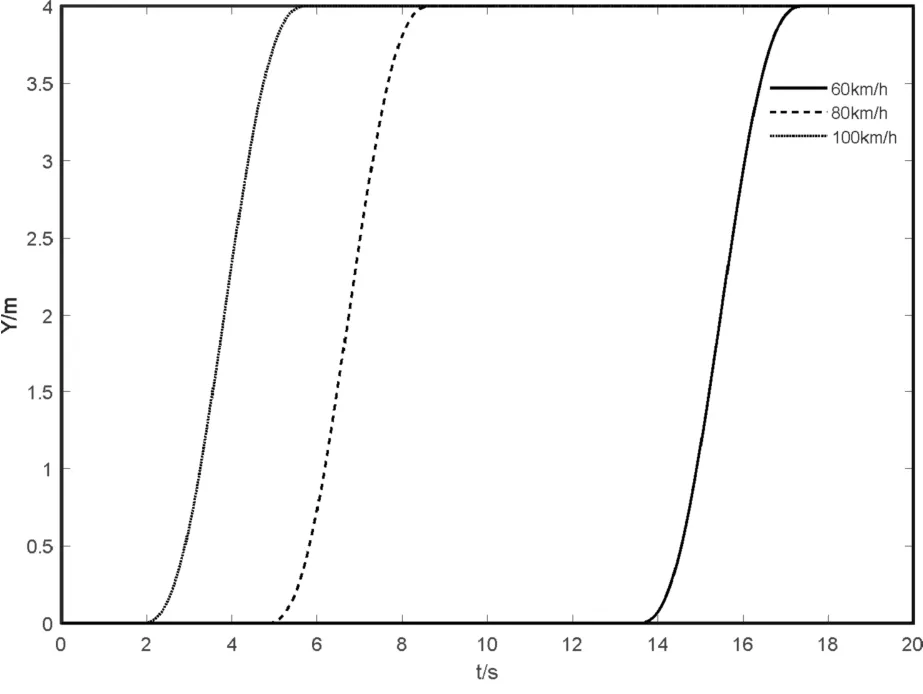
图2 不同车速下的换道轨迹

3 基于最优预瞄的换道轨迹跟踪控制器

3.1 预瞄点搜索模型

参考文献[5]建立任意道路环境下的预瞄点搜索模型，如图3所示。通过预瞄点搜索算法，可以计算出在车辆坐标系下的当前车辆位置与期望轨迹上预瞄点位置的侧向位移e。

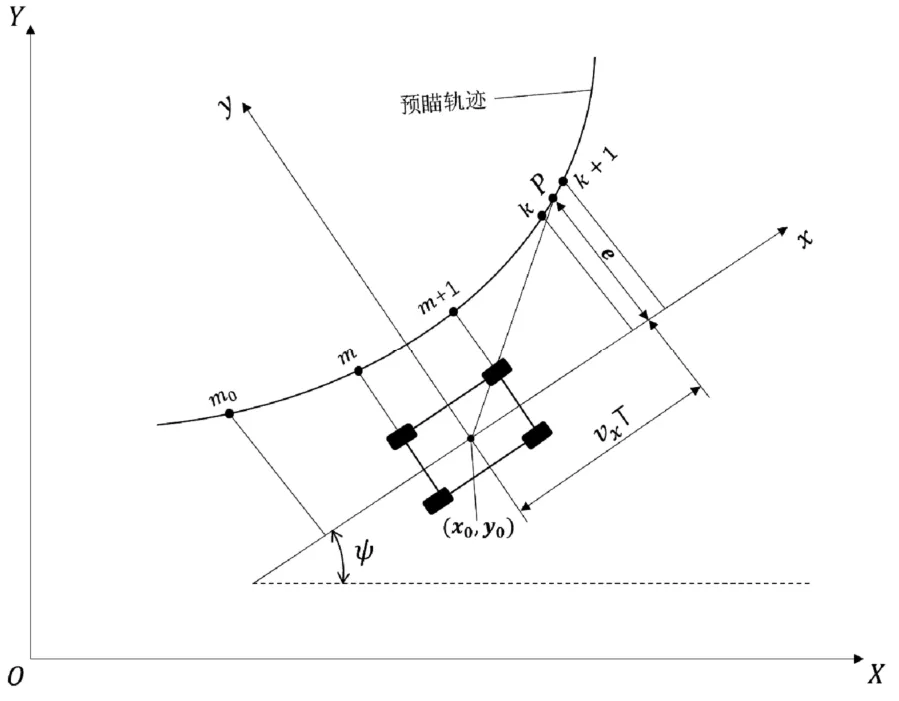
图3 预瞄点搜索模型

图3中，将期望的道路轨迹用一系列点表示，用（Xi，Yi）表示大地坐标下的轨迹点坐标，（Xi，Yi）表示车辆坐标系下的轨迹点坐标，因此可以通过式（11）进行坐标系转换：

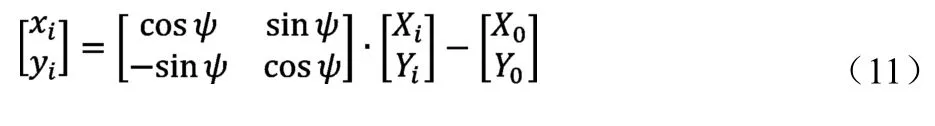
式中，ψ表示大地坐标系下的车辆航向角，（X0，Y0）表示大地坐标系下的当前车辆坐标。

设定期望道路轨迹点中离车辆当前位置后的最近点作为下次搜索的起点；将预瞄点夹在期望道路轨迹一系列点中相邻两点之间，用线性插值法计算其坐标，并进行大地坐标系到车辆坐标系的转换。由此可以得到e的计算公式：

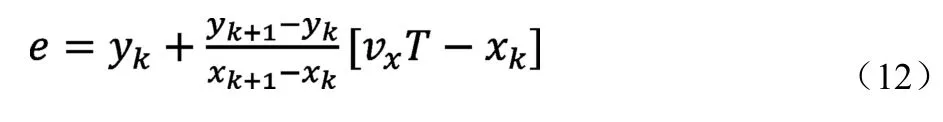
3.2 轨迹跟踪前馈控制和反馈控制

3.2.1 前馈控制

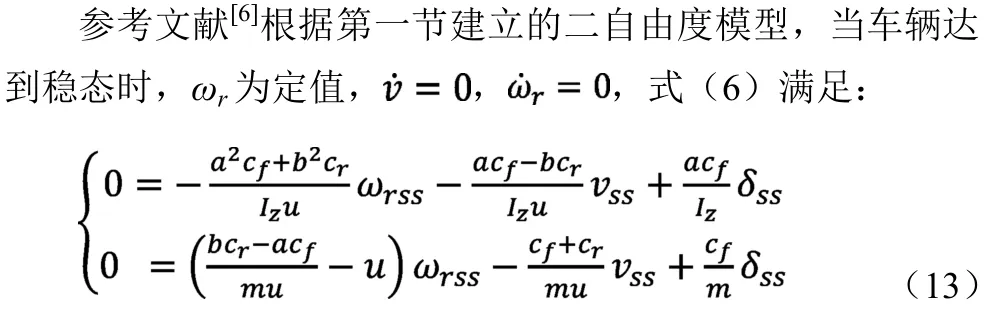
式中，ωrss、vss、δss分别表示横摆角速度、横向车速和前轮转角的稳态值。

式（13）消去δss，可得ωrss与vss的比值关系：

将式（14）代入式（13），可以得到δss和ωrss之间的传递函数：

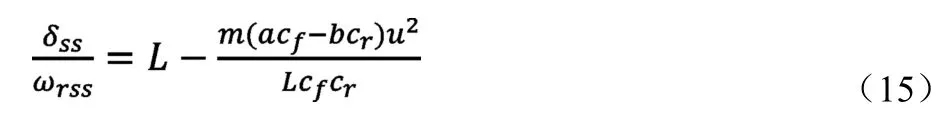
稳态情况下，汽车行驶的合速度v1ss表示为：v1ss=Rωrss。其中，R表示稳态转向半径。在车辆坐标系下，横向车速、纵向车速与合速度的关系式为：

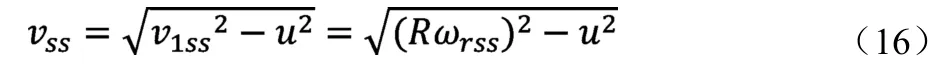
将式（16）代入式（14），整理得到ωrss的表达式：

结合车辆二自由度模型与预瞄点搜索模型，预瞄点P在车辆坐标系下的横轴投影点xP与稳态转向中心之间的距离d为：

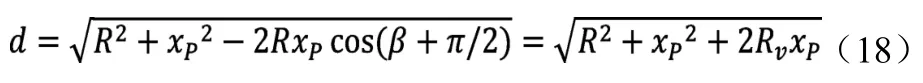
由此可知，前轮转角与预瞄误差之间的传递函数Gs为：

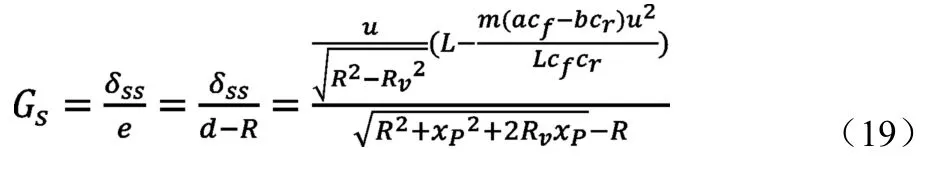
假设｜R2+2Rv xP｜≪R，Rv≪R，则Gs可近似为：

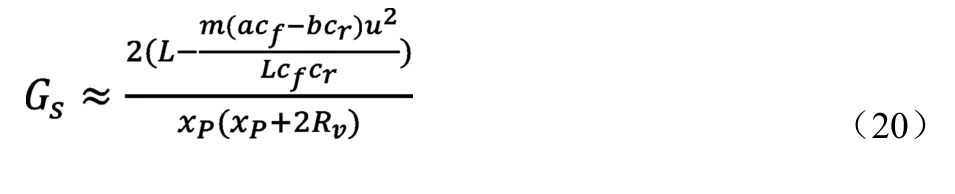
3.2.2 反馈控制

为保证控制效果和稳定性，减小航向角偏差对轨迹跟踪的影响并提高跟踪精度，基于前馈控制引入了反馈控制。反馈控制策略采用PD控制，以航向角误差作为输入，前轮转角增量作为输出，定义航向角误差为：

其中，ψP表示大地坐标系下预瞄点切线与横轴间的夹角。

由此可得，前轮转角的反馈增量为：

4 仿真试验

在道路附着系数为0.85的良好路面上，前车车速设为40 km/h，后车分别以60 km/h、80 km/h、100 km/h的车速进行换道避障仿真。车辆参数如表1所示，仿真结果如图4～图8所示。

表1 车辆参数

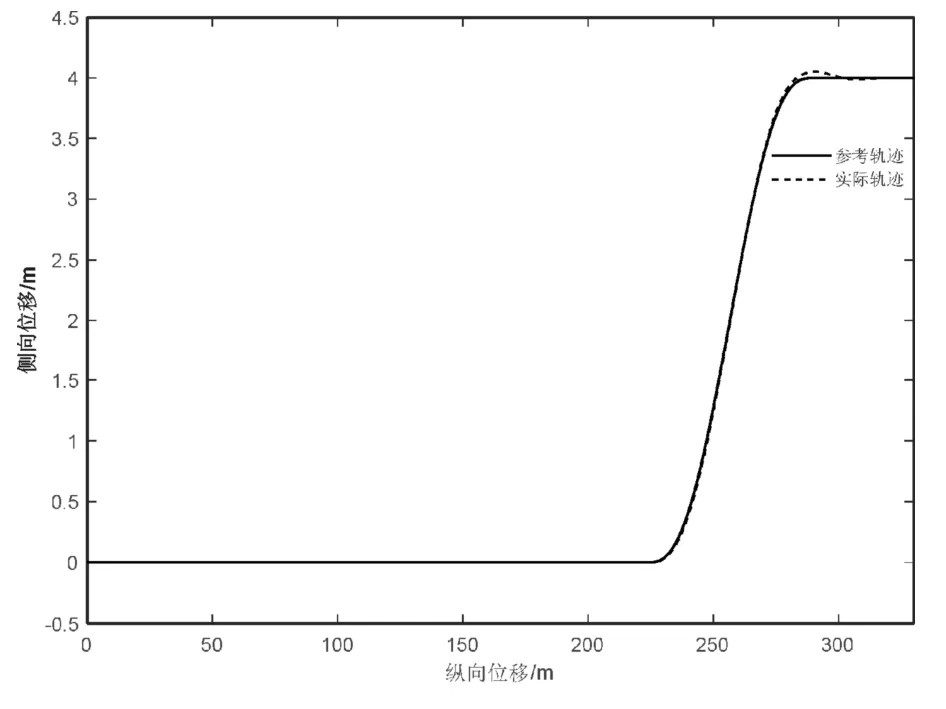
图4 60 km/h换道仿真

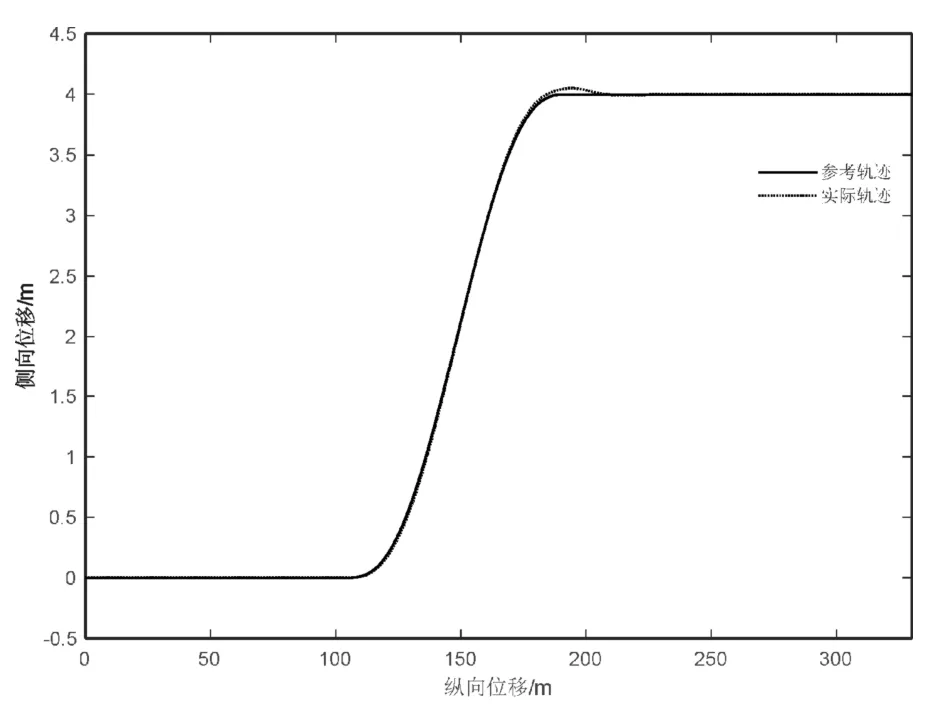
图5 80 km/h换道仿真

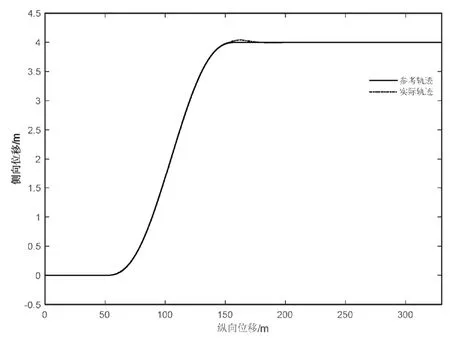
图6 100 km/h换道仿真

从图4～图7的仿真结果可以看出：不同车速下的侧向误差都保持在较小的范围内，车速60 km/h和80 km/h最大侧向偏差在0.05 m左右，当车速达到100 km/h时，最大侧向偏差为0.04 m。随着车速的增加，车辆换道轨迹跟踪过程中的侧向误差逐渐减小，说明前馈加反馈的预瞄式轨迹跟踪控制器在高速行驶情况下具有良好的适应性和较高的精度。由图8可知，方向盘转角变化的时间随着车速的增加而提前，变化的范围也逐渐减小，并且没有明显的抖动，表示控制器具有较好的稳定性，能够被执行器顺利执行。

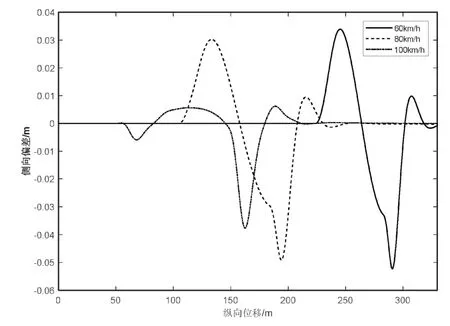
图7 不同车速下的侧向偏差

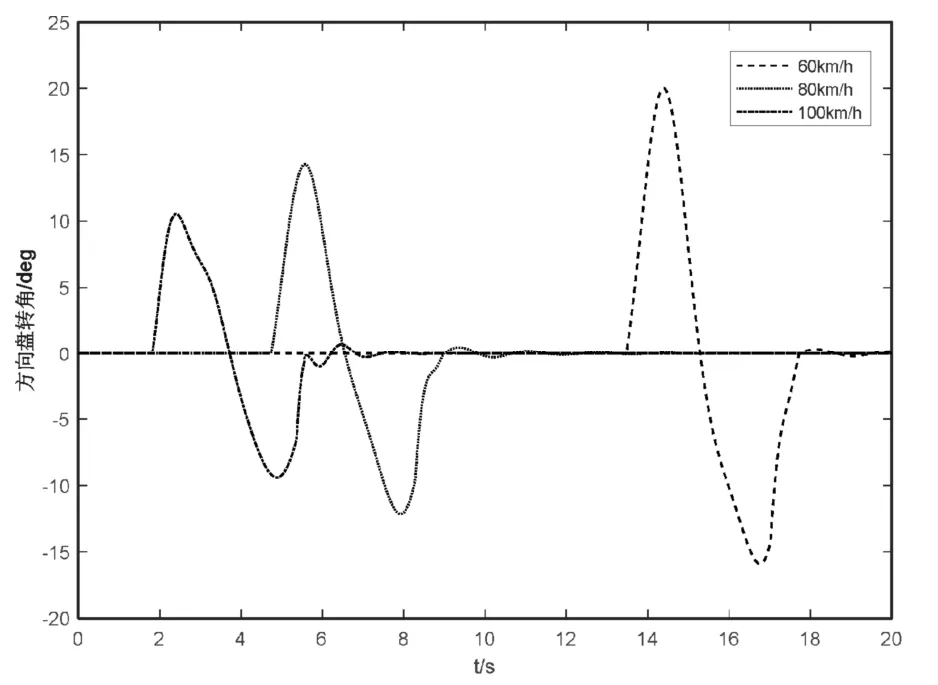
图8 不同车速下的方向盘转角

5 结束语

本文主要对高速车辆的自主换道进行模拟仿真，首先建立了简化的车辆动力学二模型，然后分析了不同的轨迹规划方法，并采用五次多项式曲线对换道轨迹进行规划。基于预瞄理论，设计前馈加反馈轨迹跟踪控制器。最后根据不同车速下的换道轨迹仿真曲线与误差分析，验证了换道轨迹跟踪控制器有着良好的跟踪性能和适应性。