基于多任务协同的粒子群聚类优化算法

颜志鹏

(广东工业大学计算机学院，广州 510006)

0 引言

多任务学习(Multi-Task Learning)[1-2]是机器学习，特别是迁移学习中的一个子领域。多任务优化(Multi-Task Optimization)[3-5]应用多任务学习优化，以研究如何有效地同时解决多个优化问题。在多任务学习中，多个相关学习任务使用(部分)共享的模型表示并同时进行训练。子问题之间也是相互关联的，通过一些共享因素实现知识迁移从而有效促进单个任务的学习效率和泛化能力。

多任务优化和多目标优化[6-7]之间有相似的地方，但存在根本性的差异。多任务优化的目的是利用种群间个体在多个不同任务之间同时搜索各个目标值对应的最优值，利用潜在的遗传互补性实现互相之间的迁移学习；多目标优化则试图解决同一个任务下竞争目标之间的冲突，寻找帕累托前沿上所有的解[8]。如图1的最小值优化问题，在多目标优化中，P2、P3、P4和P5组成了帕累托前沿，它们被认为是当前解集合中互不支配的最优解；而在多任务进化中，P1、P2、P5和P6组成了最优解，因为这些解都各自有一个目标值达到了最小值。

图1 动态演示程序界面

多任务优化最早用于进化算法中的是多任务进化算法(Evolutionary Multi-Tasking)[9]，它将多任务学习的方法结合进化算法来解决各类优化问题。Gupta等人[9]提出了多因子进化算法MFEA(Multi-Factorial Evolution Algorithm)，在测试了多因子进化算法效果后验证了多因子进化算法的有效性，证明新算法比单一目标优化更快收敛，更容易找到全局最优值。多因子进化后来得到了发展，不断有学者改进算法，也衍生出了更多新算法。Gupta等人[10]又将多因子进化算法中单任务只有单个目标拓展到每个任务具有多个目标。Liaw和Ting[11]模仿了生物共生关系为进化算法提出了一个通用的框架，并表明其性能可能比多因子进化算法更好。Cheng等人[12]提出一种多任务协同进化算法(Co-Evolutionary Multi-Tasking)。多任务优化算法可以同时优化多个目标，这点和协同进化算法类似。

聚类通过对没有标签的数据划分为若干相似对象组成的多个簇或类，使得同一类中对象间的相似度最大化，不同类中对象间的相似度最小化。有很多学者提出了基于进化算法进行的聚类，它们大多需要根据一个目标函数进行优化，包括一些经典的聚类内部指标。多目标优化也被应用于聚类问题，例如基于2个目标优化的MOCK(Multi-Objective Clustering with Automatic K-determination)算法[13-14]和基于多目标进化算法的多距离度量聚类[15]。但多目标聚类优化算法为找到帕累托前沿的所有解使用的优化目标往往需要互为冲突，找到的解个数越多，对优质解的筛选难度也越大。多任务学习可以将对不同指标的优化视作不同的任务，分别找到各个任务下最优个体并用专家知识找出最适合数据集的那个聚类指标，对结果的筛选比起基于多目标的方法更容易。

本文针对基于优化算法的聚类和其指标选择问题以自动聚类粒子群优化ACPSO(Automatic Clustering Approach Based on PSO)[16]为基础算法，提出了基于多任务协同的粒子群聚类优化算法。算法通过对多个聚类指标优化任务的学习，可以一次性得到多个指标的优化结果。实验分析发现采用多任务协同优化的方法，可以有效地得到更优的聚类结果。

1 背景

1.1 粒子群算法

粒子群优化(Particle Swarm Optimization，PSO)算法[17-18]是一种模拟鸟群的演化算法，通过记录种群中每一个粒子经过的历史最优位置和当前位置来探索全局最优解。本文算法使用的是局部邻域粒子群算法，即采用环形拓扑的粒子群结构[19]。粒子在迭代中的更新公式为：

xij(t+1)=xij(t)+vij(t+1)

(1)

vij(t+1)=ωvij+c1r1(pbestij-xij(t)+c2r2(lbestij-xij(t)

(2)

其中xij(i=1，…，m;j=1，…，d)和vij(i=1，…，m;j=1，…，d)分别对应粒子的位置和速度，m为种群中的粒子个数，d为数据维度，t为算法迭代次数，t从0开始算法逐次对整个粒子群的速度和位置向量进行迭代优化，r1和r2是0到1之间的随机数。pbesti为粒子i自身的历史最优位置，lbesti为粒子i与其邻近的粒子组成的区域局部最优位置。在头尾相连的环形拓扑结构的粒子群中，局部区域由该粒子和其前后相邻的2个粒子组成。w为惯性系数控制粒子位置更新时pbest和lbest的权重。较大的惯性系数有利于全局搜索，而较小的惯性系数一个有利局部搜索，c1和c2为加速常数，分别控制粒子朝全局最优和局部最优收敛的速度。粒子群算法可以用作聚类，如文献[20]提出的使用量子行为粒子群的动态聚类算法。

1.2 聚类评价指标

聚类集合的优劣评价指标，根据是否需要知道真实的样本分类标签，分为内部指标和外部指标。通过对数据分布的进一步研究，人们提出了一些量度数据分布特点的指标，用于聚类算法对聚类集合的优劣评价。

1.2.1 聚类内部指标

内部指标通常用于评估聚类质量或者簇划分的效果，可以用作优化算法聚类中的目标函数。本文中使用的内部指标包括分析簇划分提出的较低计算复杂度的CH(Calinski-Harabasz)指标[21]，研究模糊聚类算法提出的Dunn指标[22]，以及聚类有效性的评估方法SIL(Silhouette Statistic)指标[23]。下面给出各个指标的计算公式。

(1)CH指标

(3)

(2)Dunn指标

(4)

其中Ci代表簇i中的样本数据点组成的集合，D(Ci，Cj)代表不同类别簇i和j间的距离，该值是两个簇中最靠近的数据点之间的距离，公式表达如下：

(5)

δ(Cl)为簇l的两个最远距离点间的距离：

(6)

Dunn指标对数据噪声比较敏感，数值越大倾向于聚类效果越好。

(3)SIL指标

(7)

(8)

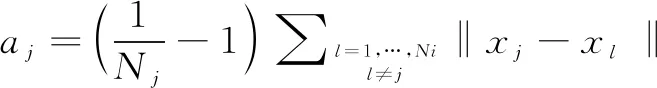
(9)

(10)

其中sj代表数据点xj的轮廓宽度(Silhouette Width)，数据点x到它所属簇i的其他数据点的平均距离为aj，x到其他类别数据点的最小距离为bj。

SIL指标为正数或者负数分别表示相应的划分分别是很好的聚类或者错误的聚类。SIL指标在零附近被认为对数据没有明确区分。SIL指标越大倾向于聚类效果越好。

1.2.2 聚类外部指标

聚类外部指标的计算需要知道真实分类情况，因此往往用于检验聚类的实际效果。本文使用聚类外部指标调整兰德系数ARI(Adjusted Rand Index)[24]作为聚类结果的质量评价。ARI是对Rand提出的聚类评价系数兰德系数(Rand Index)[25]改进后的指标，使得聚类结果在随机产生的情况下指标能接近于零。ARI假设随机模型采用广义超几何分布，将数据集N个样本真实划分表示为P，根据算法聚类得到的划分为Q，Xi和Xj为数据集的两个不同样本。现在按照这两个样本在划分P和C的分布得到以下4种不同的情形：

(1)Xi和Xj在Q中属于同一个簇，同时它们在P中也属于同一个类别；

(2)Xi和Xj在Q中属于同一个簇，但它们在P中属于不同的类别；

(3)Xi和Xj在Q中属于不同的簇，但它们在P中属于同一个类别；

(4)Xi和Xj在Q中属于不同的簇，它们在P中也不属于同一个类别。

将以上四种情形成对的样本数统计并表示为a，b，c和d，可得ARI值：

(11)

ARI为1表示两个划分之间的完美一致性，值越小表示它们之间的差异越大。其值也可以为负，表示比随机得到的分类效果还差。

2 基于多任务协同的粒子群聚类优化

这部分首先描述本文提出的基于多任务协同的ACPSO算法，简称MT-CACPSO的粒子编码及其初始化方法，然后介绍算法聚类时的聚类规则。最后给出算法的多任务协同实现具体流程。

2.1 种群个体的编码

粒子被编码为Kmax+Kmax*d维的向量，其中d是样本点的维度，Kmax是程序定义的聚类样本簇数的最大值。对于每个粒子的前Kmax个值分别代表后续Kmax个类别中心点的激活阈值。如果该值大于0.5，则对应簇的中心点被激活，相当于该簇被纳入聚类的计算，否则不被激活也就是不纳入计算。如果该值在优化过程中被修改为大于1或为负数，则重置该值为1或0，如果得到的中心点数量小于设置的最小类别数Kmin，则随机选取足够的激活阈值改为大于0.5的随机值。例如，对于一个维度d为2，最大聚类类别数Kmax为4的个体，前面4个值为激活阈值，第二个位置0.4小于0.5，因此它对应的第二个中心为未激活状态，以此类推，其他位置的阈值大于0.5从而被激活。因此，这个个体的聚类簇数目为3。

2.2 种群的初始化

每个个体的激活阈值控制着聚类数目，为了让种群的所有个体不会因随机性出现偏向，在初始化时会让个体从最小聚类数Kmin到Kmax均匀分布，因此要控制激活阈值部分的编码，其余位置则随机设置为数据各维度所处的范围内。种群所有个体的初始聚类数K在Kmin到Kmax间呈均匀分布。

2.3 聚类规则

传统的粒子群优化方式应用于聚类优化时，对于聚类形态非圆形的聚类问题，效果不佳。文献[16]提出NMP(Nearest Multiple Prototypes)规则用于提升聚类优化中的性能。

首先，每个样本被分配到最近的簇中，所有被分配到同一个簇的样本组成了一个候选样本集。这里，我们把这个簇称为这些样本的一个未确定簇。然后，对每一个簇，从候选样本集中选一个最近的样本，所有簇的这种最近样本点合并称为最近样本集。最后，在最近样本集中找到一个样本，这个样本离它所在的未确定簇距离是最近样本集中最小的，就将该样本分配到它的未确定簇中。不断重复上述步骤直到所有样本被分配完毕。相比确定样本所在类别的传统方法，NMP是一个动态的过程，更加灵活。

2.4 多任务协同优化

多任务协同优化[12]不仅有多任务的特性，还使用了协同进化让两个子群进行交流，而不是对单个种群的优化。本文对算法进行了调整，能够对更多优化任务进行优化，实验中的任务数等于聚类优化任务中的指标个数。下文中用集合S表示整个种群，它由被L个任务分割的子种群sk(k=1，2，…，L)组成，即S={s1，s2，…，sL}。

2.4.1 不同优化任务间粒子群的协同进化

在某个优化任务下的粒子群，如果在对其指标优化任务的搜索陷入停滞时则激活该步骤进行跨任务的知识转移，将粒子的位置偏向另一个被随机选中的任务的全局最优位置。

假设某个优化任务序号为k，来自该任务的种群内的某个粒子为xi(k)，粒子的个体最优值在经历γ1次迭代后依然没找到更优的个体最优值，将对该粒子编码执行下面的更新操作：

(12)

其中，r1和r2都是[0，1]之间的随机变量，r3∈[1，L]，且r3≠k，而gbest(r3)表示另一个随机选中的任务r3的全局最优位置，j=1，2，…，d(d表示粒子编码的维度个数)。如果粒子更新后得到的优化指标比粒子的历史最优值更好则更新历史最优位置，否则不更新。

2.4.2 优化任务内的粒子间杂交

某个种群所代表的优化任务在γ2次迭代后依然没找到更优的全局最优位置时会随机从该种群内抽取2个粒子进行杂交，如果杂交得到的后代的适应值大于当前粒子的适应值，则用杂交得到的后代替换父代。杂交的更新公式如下：

(13)

(14)

2.5 MT-CACPSO具体流程

本算法包括4个主要步骤，下面以最大化问题为例展示算法流程下：

输入：数据特征。

输出：L个指标下对应的聚类结果。

a) 读入数据集并做归一化处理，为L个优化指标产生L个个体数为m的粒子群s1，s2，…，sL并初始化；

b) 评估更新每个任务k下每个粒子的pbesti和lbesti(i=1，2，…，m)，k=1，2，…，L;

c) 获取各个任务的当前的全局最优位置gbestk(迭代次数t←0)，k=1，2，…，L；

e)while(t没有达到最大迭代次数)t←t+1；

fork=1，2，…，Ldo

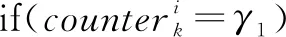
更新完该种群下所有粒子后，获取任务k的全局最优位置gbestk的适应值fk(t)；

if(fk(t)≤fk(t-1))counterk←counterk+1；

if(counterk=γ2)在该任务粒子群中随机抽取2个粒子根据公式(13)和(14)进行杂交；counterk=0；

f) 输出各个任务的全局最优位置作为结果。

在上述步骤中，共有L个粒子种群，分别对应前文提到的L个内部聚类指标。当种群内的粒子陷入停滞时将使用公式(12)更新粒子位置实现种群间的协同进化。判断粒子是否停滞需要先设定一个系统参数γ1，当某个粒子经历了γ1次迭代后依然无法获取到更优的适应值才执行该步骤。此外，某个粒子群的全局最优在经历γ2次迭代后没有获得新的全局最优位置将在该粒子群内进行内部的杂交。

3 算法实验测试

3.1 测试数据集

数据集选用了人工数据和真实数据，表1中Banknotes和Vertebral Column数据集为真实数据集，它们来自UCI 机器学习数据集(http://archive.ics.uci.edu/ml/index.html)。

表1 测试的数据集

表1中序号3到12的数据集均为人工数据，它们有着不一样的形状的簇，是通过由Handl和Knowles提出的簇生成器[13]得到的，生成器为高维的椭圆形簇，长轴方向上任意分布，2d4c代表这个数据集维度为2，类别数为4。

3.2 参数设置

本实验比较了3种聚类算法。其中ACPSO是单任务算法，实验中分别对其采用了不同的聚类内部指标作为优化目标进行测试。ACPSO的种群规模为40，本文提出的MT-CACPSO同时优化多个内部指标任务，每个任务的种群规模为40。最大聚类数Kmax为30，最小聚类数Kmin为2。惯性系数w为0.75，加速度常数c1和c2为2，粒子的最大速度控制在数据范围的20%内。系统参数γ1=γ2=15。

实验将MFEA算法用于聚类，即多因子进化聚类算法。MFEA算法的RMP(Random Mating Probability)控制着不同任务之间交流程度，取值范围为(0，1)，值越大则跨任务间的交流越频繁[9]。本文实验中RMP参数取值为0.3。以上3种算法最大迭代次数都为2000次，每个算法都独立运行10次。

3.3 MT-CACPSO与单任务算法的结果比较

ACPSO是先后选取了不同的3个优化目标(CH、DUNN、SIL)单独运行而得到的结果，MT-CACPSO是一次运行后得到的3个不同优化任务对应的结果。

表2比较了MT-CACPSO和单任务的ACPSO的实验结果的内部指标，结果取10次运行的平均值。其中，加粗的结果为同一个内部指标下，两种算法的优胜结果。多任务MT-CACPSO算法比单任务ACPSO算法获得更多的优胜解。例如在CH指标上，MT-CACPSO算法在12个实例中有7个实例找到更优的解，而ACPSO算法有6个实例找到了更优的解，其中主要是在维度相对低的数据集上MT-CACPSO表现更优。而在DUNN和SIL指标的优化中，MT-CACPSO算法获得更多的最优解。在对DUNN指标的优化结果中，MT-CACPSO的优化得到的指标值大都不低于单任务ACPSO，只有2d20c例外，在SIL指标上大部分数据集也优于ACPSO的优化结果，说明MT-CACPSO在这些指标的优化任务上，发生了不同优化任务间的知识迁移，从而得到更好的收敛结果。

表2 ACPSO与MT-CACPSO运行结果的平均内部指标

续上表

表3给出了两种算法的外部聚类指标结果。基于多目标的聚类方法[13-14]中得到的帕累托前沿上所有聚类结果需要进行筛选，类似的，由于使用了多个指标，所以采用多任务的聚类方法也需要引入专家知识对结果进行筛选，而且因为解集个数只等于优化目标个数，所以筛选难度低于基于多目标的方法。通过引入专家知识，我们将最合适该数据集的结果作为最终的聚类结果，表格中加粗的结果表示同一行中最优的ARI值。

对于真实数据集Banknotes和Vertebral Column，MT-CACPSO的CH指标优化任务取得了更好的聚类结果。人工数据集2d4c两个算法的结果一样，在DUNN指标优化上获得了最优结果。其余人工数据集中MT-CACPSO有6个更优的聚类结果，ACPSO则是3个，其中2d10c是SIL优化任务获得了最好的结果，其他数据集则是CH指标优化结果更好。这体现了不同指标优化对于同一个数据集的不同影响。

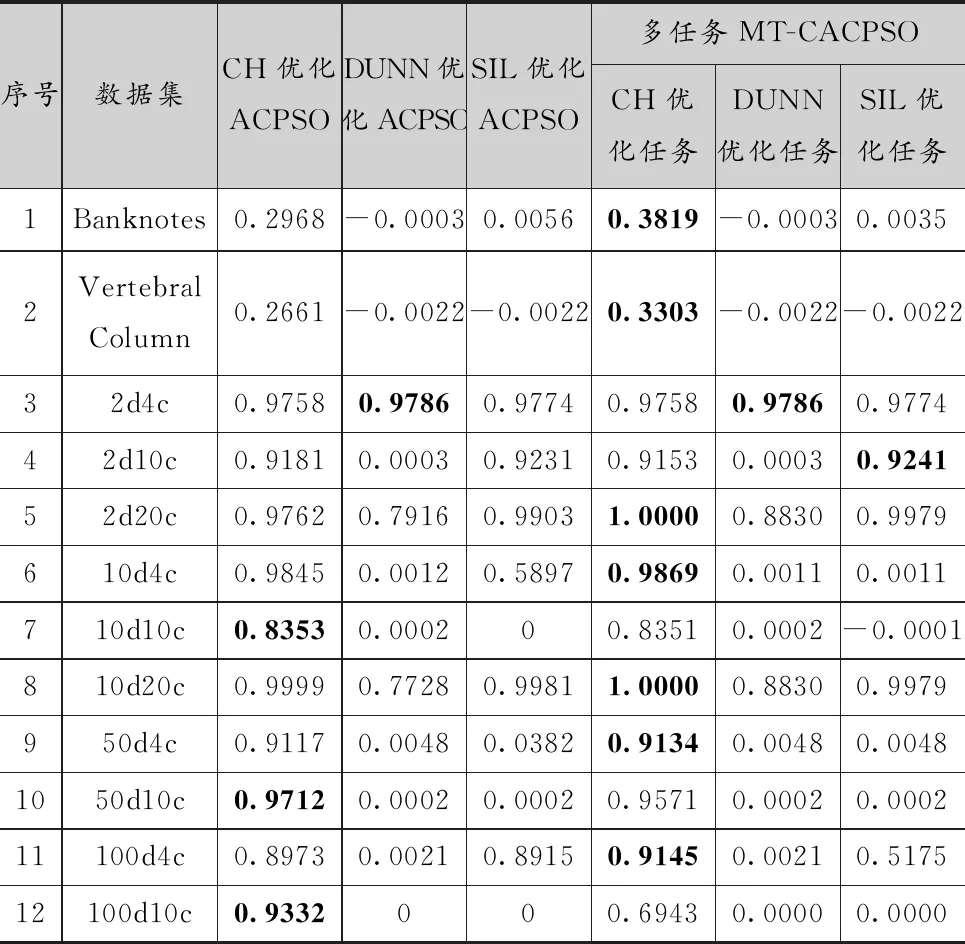
表3 ACPSO与MT-CACPSO运行结果的平均外部指标ARI

3.4 MT-CACPSO与多因子进化聚类算法的结果比较

表4和表5比较了MT-CACPSO和多因子进化聚类(MFEA)算法的实验结果，每个算法共运行了10遍，结果取十次运行的平均值，两个多任务聚类算法都是一次运行后得到的3个不同优化任务对应的结果。两种算法都是基于多任务的聚类算法，该实验的结果体现了采用协同多任务相对于多因子进化算法的优势。

表4给出的是两个算法结果的内部聚类指标，加粗的结果为同一个内部指标下，两种算法的优胜结果。经过对比，MT-CACPSO在3个指标的优化上都获得了比多因子进化聚类算法更多的优胜次数。其中，在3个指标优化上MT-CACPSO分别获得了10、10、11次最优解，而多因子进化聚类算法是3、7、3次。在CH指标优化任务上，MT-CACPSO的结果优越性主要体现于适合使用CH指标优化的超球形或超椭圆形簇人工数据集(序号3到12)，除2d20c外均取得了最优的解。在DUNN指标的优化上MT-CACPSO只有2d20c和10d20c这2个实例没有取得最优解。SIL指标优化上MT-CACPSO除2d20c外的实例上都获得了最优解。综上，使用环形拓扑粒子群的协同多任务算法获得了更好的收敛结果，是比多因子进化算法更加容易突破局部最优值的多任务优化算法。

表4 多因子进化聚类算法与MT-CACPSO运行结果的平均内部指标

表5中给出了多因子聚类算法和MT-CACPSO的聚类结果的外部指标，加粗的结果表示同一行中最优的ARI值。真实数据集中，MT-CACPSO聚类结果均取得了最优解。人工数据集中，除2d4c、10d20c和100d4c外，MT-CACPSO均获得比多因子进化聚类算法更优的聚类结果，其中10d20c则是两种算法都获得了完全正确的聚类结果。可以看出，基于多任务协同的聚类算法的聚类效果优于多因子进化聚类算法。

表5 MT-CACPSO与多因子进化聚类算法结果的平均外部ARI值

3.5 算法收敛曲线图

图2选取了个别有代表性的数据集，并画出了3个算法在各个优化指标下的收敛曲线，结果取十次运行的平均值。在2d10c的CH指标优化中，ACPSO在前期的迭代中收敛速度最快，但后续的迭代中MT-CACPSO通过不同任务间的交流实现了局部最小值的突破从而得到了更优的CH指标结果。在10d20c数据集Dunn优化和10d4c数据集SIL优化中，两种基于多任务的聚类算法都在前期迭代中得到了比ACPSO更优的目标值，而MT-CACPSO的收敛性能又好于多因子聚类算法。

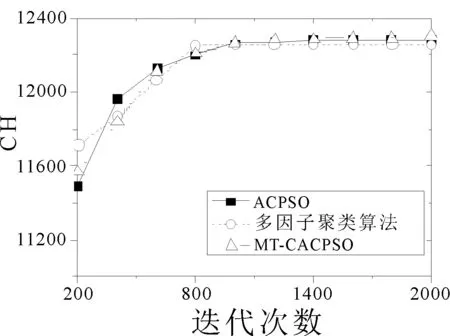
(a) 2d10c CH指标收敛曲线

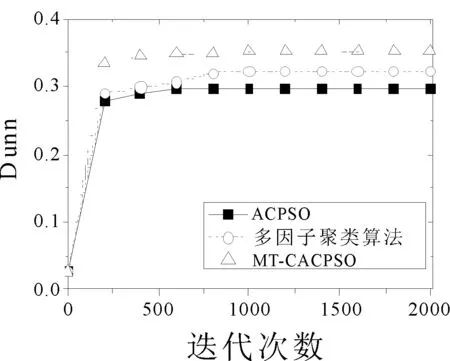
(b) 10d20c Dunn指标收敛曲线

(c) 10d4c SIL指标收敛曲线

4 结语

本文中提出了基于多任务的聚类算法MT-CACPSO，并与单任务的ACPSO和同样是基于多任务优化的多因子进化聚类算法进行了比较。虽然不同内部指标适用于不同数据集，但基于多任务的聚类算法同时完成对3个不同内部指标的优化后可以用专家知识从中选出一个最优的聚类结果。通过与单任务ACPSO的聚类算法结果对比发现，多任务聚类算法受益于多个指标的不同环境，有机会通过任务间的知识迁移获得更好的聚类结果。与多因子进化聚类算法的结果对比则说明基于协同多任务进化的聚类算法优于基于多因子进化的聚类算法。