基于仿射运动模型的运动矢量的教学视频水印算法

马宏茹，李 硕，纪 宁

（大连交通大学 信息学院，辽宁 大连 116021）

0 引 言

教学视频是现代教育的主要教育资源形式之一，也是远程视频的学习载体之一。教学视频是指通过专用的录像软件，将教学过程中教师在电脑屏幕上实时演示和讲课的内容录制下来，并且整合教师的声音和画面等信息生成视频文件，供学习者使用的教学资源[1]。然而，目前网上盗版视频较多，有些不良商家甚至打着教学视频的旗号传播非教学视频内容，给社会和学习者造成不良的影响。为了保护教学视频的版权和产权，数字水印技术（Digital Watermarking）作为一项成熟的技术，可以广泛应用到教学视频保护领域。

视频码流的运动矢量是通过视频编码的运动估计算法获得的[2-3]，因此，将水印信息嵌入运动矢量，在视频编码的同时即可完成水印的嵌入。Kutter等人首次提到了基于运动矢量的视频水印嵌入方案，主要利用对运动矢量进行适当修改，进而起到嵌入水印信息的效果。文献[4]在此基础上进一步拓展了基于运动矢量的视频水印技术。由此可见，准确的运动矢量对视频水印嵌入与提取起着至关重要的作用。但是以上基于运动矢量的视频水印技术都是在传统编码标准上完成的，而传统编码标准中运动矢量的生成都是基于平移运动模型，无法有效预测视频中运动物体旋转和变形等一系列复杂运动，这势必会造成运动矢量不准确，进而造成水印嵌入和提取的不准确。

本文从实际应用出发，结合传统的运动矢量的视频水印技术的优缺点，提出一种基于仿射运动模型的运动矢量的视频水印算法。该水印算法在仿射运动模型的基础上得到准确的运动矢量，在编码过程中对运动矢量嵌入水印，在视频解码过程中提取水印。

1 基于仿射运动模型的运动矢量生成策略

1.1 仿射运动模型

视频编码中，运动矢量的生成过程即是运动估计的过程，如图1所示。

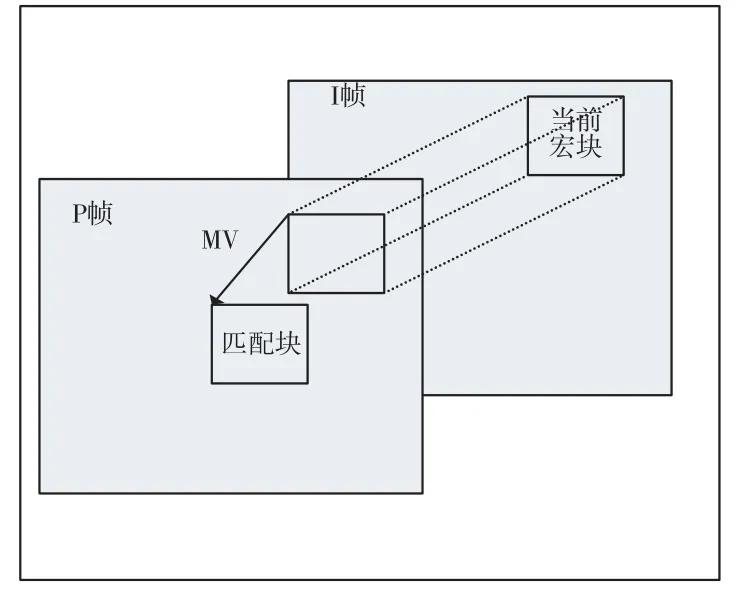
图1 运动估计过程

即最小化如下的公式：

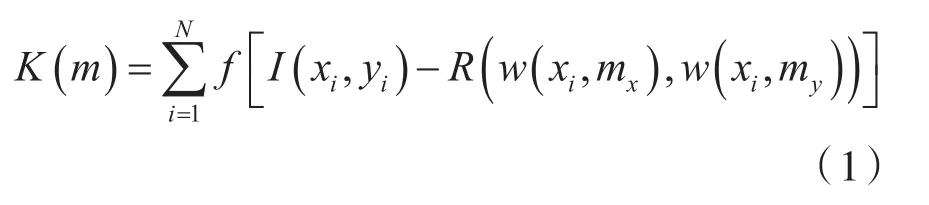
用P表示视频序列中的参考帧；I表示当前帧；N表示视频帧的像素总数；f(·)表示匹配误差某种度量标准，如绝对误差和SAD、平均绝对差值MAD（Mean Absolute Difference）、误差平方和SSD（Sum of Squared Difference）以及均方误差MSD等。w表示为形变函数，即运动模型；mx和my分别表示为该运动模型下的运动矢量沿x轴和y轴方向的分量。传统的视频编码中块平移运动模型为w(xi,m)=xi+mx和w(yi,v)=yi+my。

仿射运动模型对应的函数为：

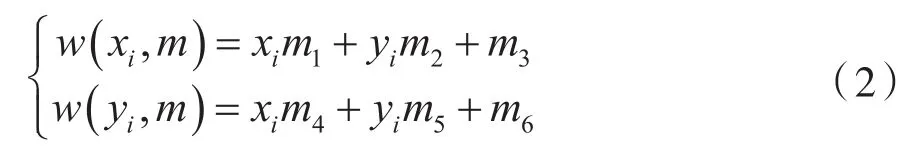
式中：(m1,m2,m3,m4,m5,m6)为仿射模型的运动矢量，m1、m2、m4、m5与旋转、缩放运动有关，而m3、m6与平移运动有关。为了方便求解，本文选取SSD作为匹配误差的度标准，即：

式中：匹配误差ei(m)=I(xi,yi)-R(w(xi,m),w(yi,m))。

1.2 牛顿迭代法求解策略

本节利用高斯-牛顿迭代法（Gauss-Newton gradient-method），基于仿射运动模型，求解出视频编码中当前宏块的运动矢量。高斯-牛顿法作为最优化方法的一种，已经被广泛运用到图像处理和视频编码中[5]。其求解过程就是找出最小化K(m)的运动矢量。首先采用泰勒展开式（Taylor）对匹配误差函数进行近似，从而通过反复迭代求出极小值。假设当前迭代点是mk(k=1,2,3,4,5,6)，那么可以用匹配误差函数ei(m)在mk处的一阶泰勒展开式近似ei(m)，可得：

式中：Δm=mk+1-mk；mk+1表示下一次迭代点；ei´(mk)表示ei(m)在mk的 1阶导数，将式（4）代入式（3），可得SSD泰勒表达式：

K(m+Δm)对更新参数Δm的偏微分为：

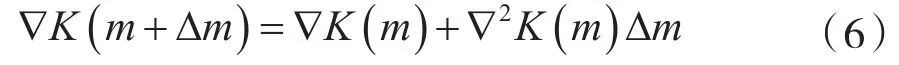
进而可得：

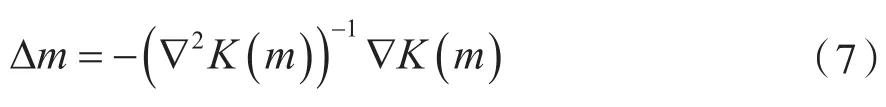
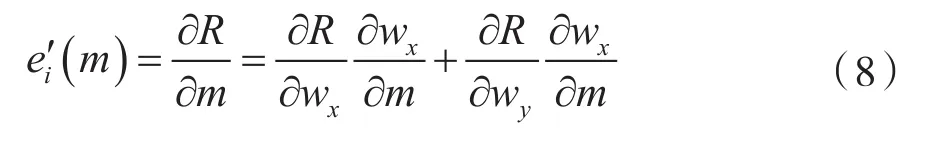
2 基于运动矢量的水印选择嵌入与提取算法

运动矢量是直接影响视频传输质量的因素之一，因此基于运动矢量的视频水印技术对运动矢量的准确性要求很高[6]。本文通过基于仿射运动模型的高斯-牛顿迭代法求解运动矢量策略，较传统视频编码中平移运动模型，可得到更为准确的运动矢量。

2.1 视频水印嵌入

在新一代的编码标准HEVC（High Efficiency Video Coding）中，当前宏块的运动矢量的预测与上、下、左、右4个宏块的相关性很大。由于运动矢量影响最终视频解码质量，应当尽量小幅度地修改运动矢量，因此本文只在与平移运动相关的运动矢量m3、m6进行水印嵌入。文献[7]提出压缩视频序列中大部分帧是运动补偿编码帧，因此将水印隐藏在幅度值大运动矢量中具有较好的鲁棒性。综合上述特性，提出一种水印嵌入思想：在HEVC编码中每个图像组（GOP）可以自定义，本文采用每隔一个Gopsize=4进行一次水印嵌入操作。水印信息是一幅二值图像，通过一定的控制条件选择其中的部分运动矢量来嵌入水印。嵌入算法为：首先根据周围宏块的水平和竖直运动矢量分量的平均值，分别定义当前宏块的运动矢量阈值ρx和ρy，根据ρx和ρy的值确定是否在运动矢量的水平分量或垂直分量嵌入水印。该算法只需要对运动矢量进行简单的判断和加减运算，因此计算复杂度较低。

比较当前宏块的水平和竖直运动矢量分量ρx和ρy，选取阈值较大为水印嵌入控制条件。然后，比较当前宏块运动矢量分量是否满足条件，若满足，当前分组运动矢量分量嵌入1比特信息，否则跳到下一分组。其步骤简述如下。

（1）确定模板的位置，通过基于仿射运动模型的运动矢量求解法求解周围运动矢量分量m3和m6，以便计算ρx和ρy。

（2）通过比较ρx和ρy，确定该组模板嵌入水印控制阈值，判断是在水平分量还是垂直运动矢量嵌入水印。

（3）根据确定的控制阈值，若|m(i,j)|＞ρ，则水印序列βk=1，否则βk=0。其中βk表示第k个水印值；若|m(i,j)|≤ρ，则不满足水印嵌入条件，跳到下一分组。

（4）判断水印是否嵌入结束。

整个水印嵌入过程如图2所示。由ρx、ρy可知，水印嵌入充分利用周围宏块的运动矢量，且只对运动矢量的某一分量进行微调整。

图2 本文视频水印整体框架

2.2 水印提取算法

相对于水印嵌入算法，水印的提取可以在解码端同步进行。首先提取当前宏块的周围4个宏块的运动矢量，按照嵌入时的方法计算ρx和ρy，提取的步骤如下。

（1）比较ρx和ρy，选取较大值作为嵌入水印阈值ρ，确定水印嵌入在水平运动矢量m3还是竖直运动矢量m6中。

（2）依照下面的公式提取水印：

通过上述水印提取步骤即可提取水印。

3 结 语

本文主要针对传统基于平移运动模型的运动矢量视频水印算法提出一种改进的运动矢量水印算法。利用仿射运动模型，通过高斯-牛顿迭代法生成更为准确的运动矢量，进而根据当前宏块与周围宏块的运动相关性选择嵌入水印。实验结果表明，这种方法在提高视频质量的同时，水印的嵌入与提取更为准确。但是本文的算法具有一定的复杂性，在视频编码后导致码率有一定的增加，后续的工作将继续改进。