神经网络滑模控制下肢外骨骼机器人的轨迹跟踪

张敬宇,曹佃国,曹金鑫,张佃聪,王加帅,陈 曦

(曲阜师范大学工学院,山东 日照 276800)

0 引言

下肢外骨骼机器人具有精确、灵活性及柔性等特点,可以很好地帮助患者进行康复训练[1]。 经过多年的发展,国内外已经在下肢外骨骼领域取得了很大的进展。 瑞士Hocoma 公司设计了可投入商用的Lokomat 康复机器人[2]。 美国加州大学研发的BLEEX机器人,采用了液压驱动的方式,在控制算法上采用了灵敏度放大控制[3]。 日本筑波大学研发的HAL-3 机器人,将脑电-肌电信号用于机器人控制,大大提高了人机交互能力[4]。 我国在下肢外骨骼机器人方面也取得了一定的进展。 电子科技大学研制出的下肢外骨骼机器人样机,能够有效地感知穿戴者的运动意图[5]。 中科院深圳先进技术研究院经过长时间的理论设计与研发,研制了一款用于下肢康复的可穿戴式外骨骼设备[6]。

下肢外骨骼机器人的运动需要合适的控制算法,保证机器人在运动过程中的稳定性及鲁棒性。 常见的比例积分微分(proportional integral differential,PID)控制算法应用于控制下肢外骨骼机器人[7],例如神经网络PID 控制。 灵敏度放大控制需要精确的运动学模型,并且会放大干扰,导致外骨骼机器人的不稳定[8]。 双足机器人零力矩点(zero moment point,ZMP)和线性二次调节器(linear quadratic regulator,LQR)完成对特定轨迹控制的跟踪,具有良好的跟踪效果[9]。 外骨骼机器人系统滑模控制具有高鲁棒性和实现简单等特性[10],但天生的抖振特性在一定程度上影响了控制效果。

本文在利用拉格朗日法建立了下肢外骨骼机器人三连杆模型的基础上,设计了基于自适应神经网络滑模的下肢外骨骼机器人控制算法。 该算法引入径向基函数(radial basis function,RBF)神经网络逼近模型不确定项。 由于滑模控制具有抖振特性,因此提出了一种改进的趋近律,削弱了抖振对控制效果的影响。 通过仿真,验证了该控制方法具有良好的跟踪效果,提高了行走的稳定性。

1 下肢外骨骼机器人建模

在建立下肢外骨骼模型时,不仅要考虑髋关节和膝关节,还要将踝关节作为一个自由度,因此以三连杆机构为模型对下肢外骨骼进行建模。 图1 所示为下肢外骨骼机器人研究平台和三连杆机构模型。 该模型在髋关节处建立坐标系统。 外骨骼机器人的大腿质量为m1,长度为L1;小腿的质量为m2,长度为L2;脚掌质量为m3,长度为L3;θ1、θ2和θ3分别表示髋关节、膝关节和踝关节转过的角度。 本文采用拉格朗日法,建立以下下肢外骨骼机器人动力学方程。

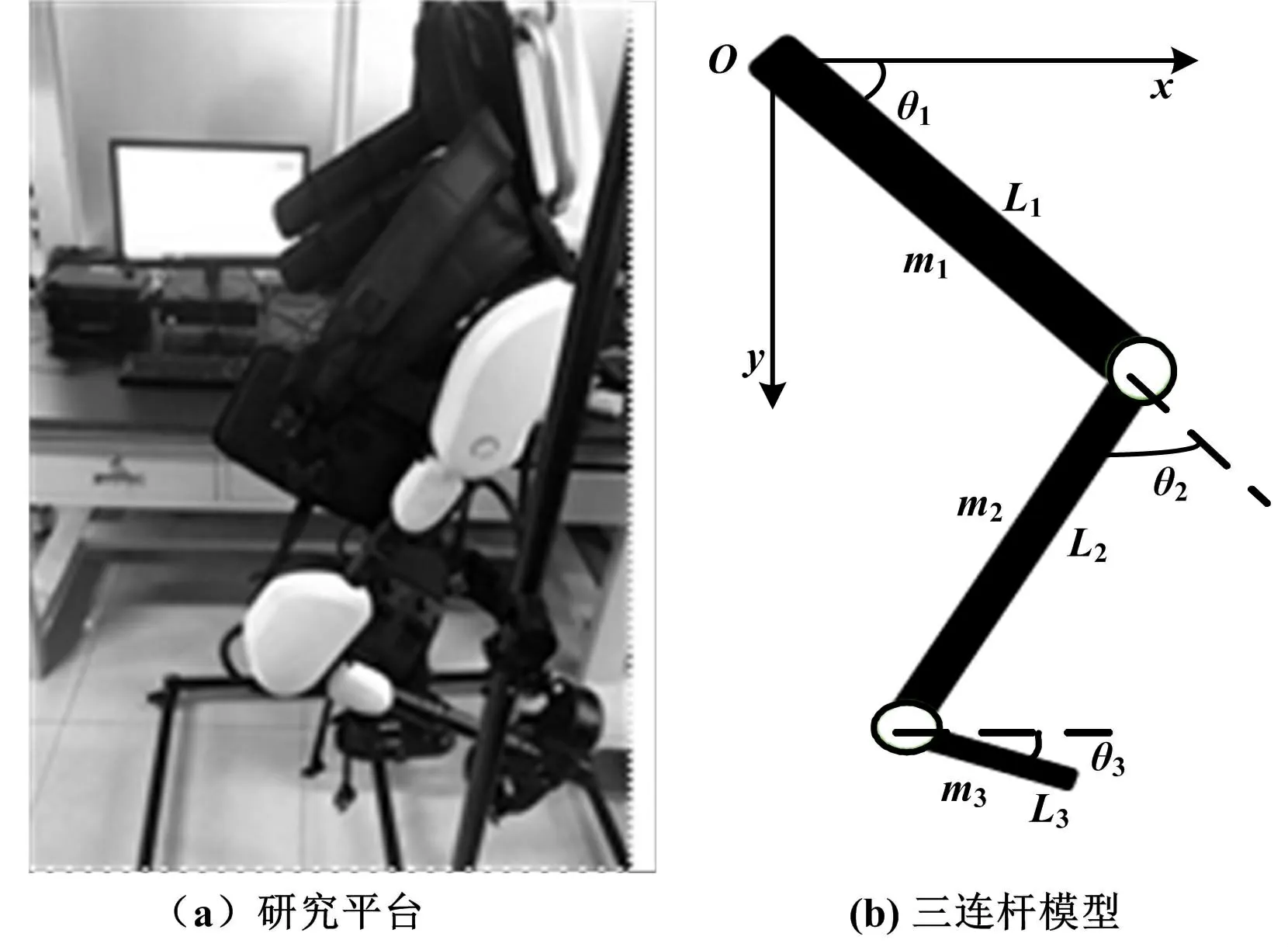
图1 下肢外骨骼机器人研究平台和三连杆机构模型Fig.1 Research platform of lower limb exoskeleton robot and three-link mechanism model

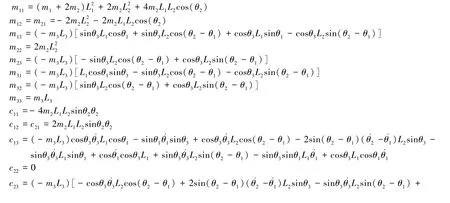
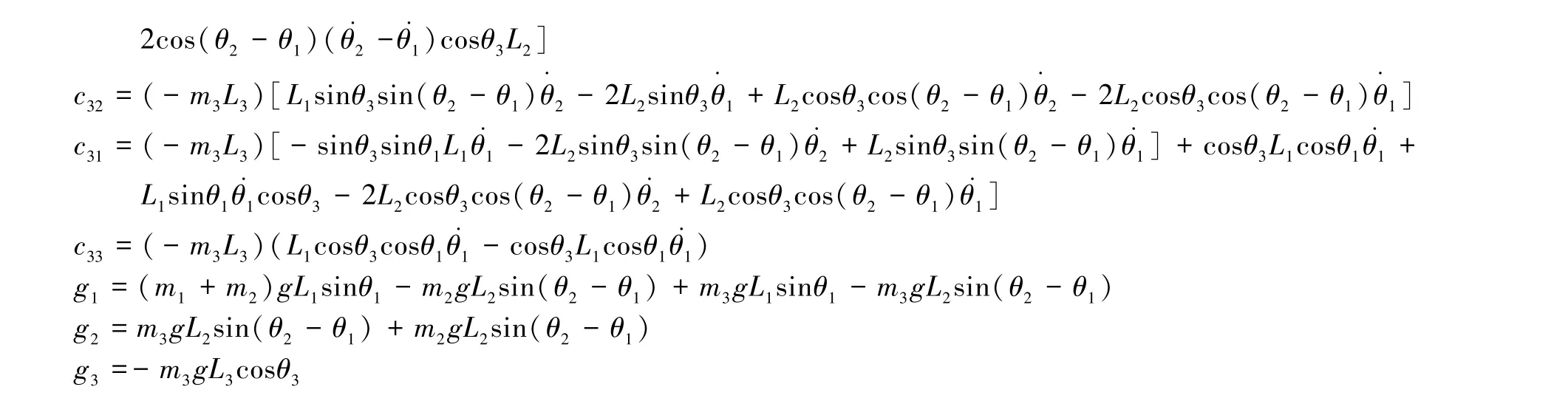
根据下肢外骨骼机器人的动力学方程,若已知各关节角度、速度和加速度,可以解出各个关节所需的力矩[12]。 机构力和关节变量之间的关系为后续的控制方法设计提供了理论基础。

2 下肢外骨骼机器人控制器设计

滑模控制适用于非线性系统的控制与应用,在设计时无需考虑环境参数变化和外界干扰,具有响应速度快、可靠性高和实现简单等特点。 该设计方法在工业控制中得到了广泛的应用。 以三连杆为模型的下肢外骨骼机器人很容易受到环境干扰,导致轨迹跟踪不精确、跟踪误差变大。 滑模控制能有效地解决该问题。

为了提高下肢外骨骼机器人行走过程中的鲁棒性,要加大切换增益。 但这会产生抖振问题。 此外,动力学模型中的M(q),C(q,q·)和G(q)参数必须精确,而实际过程很难做到。 故引入RBF 神经网络逼近未知模型[13],并提出一种改进的趋近律,以提高机器人行走稳定性,从而有效解决控制输入的抖振问题。

图2 所示为基于RBF 神经网络自适应滑模控制的下肢外骨骼机器人控制框图。 系统的输入为给定的期望轨迹,输出为实际轨迹。x为RBF 神经网络的输入,参数根据未知模型来选择,输出为未知模型的逼近项。 通过改进的趋近律结合神经网络组成滑模控制器。 控制器的输出u能提供合适的力矩,使关节跟踪期望的轨迹,保证误差在很小范围内。

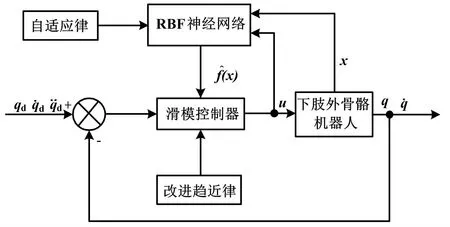
图2 基于RBF 神经网络自适应滑模控制的下肢外骨骼机器人控制框图Fig.2 Control block diagram of lower limb exoskeleton robot based on RBF neural network self-adaptive sliding mode control

2.1 自适应神经网络滑模控制器设计

考虑摩擦和未知干扰的下肢外骨骼机器人的模型形式如下:

式中:x为网络函数的输入;g为网络的输出;j为网络隐含层中的第j个节点;h=[hj]T为网络的高斯基函数输出;c、b为高斯基的中心值和基宽;W*为网络的权值;ε为网络的逼近误差,并且‖ε‖≤‖εN‖。

根据未知模型的表达式,网络的输入为:

网络的输出为:

式中:f^(x)为f(x)的估计值。

设计控制率为:

2.2 稳定性分析

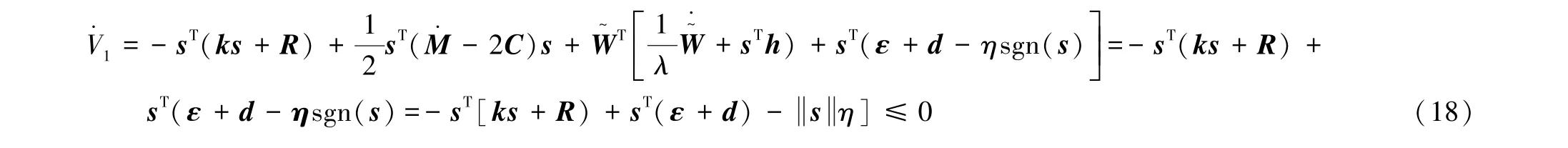
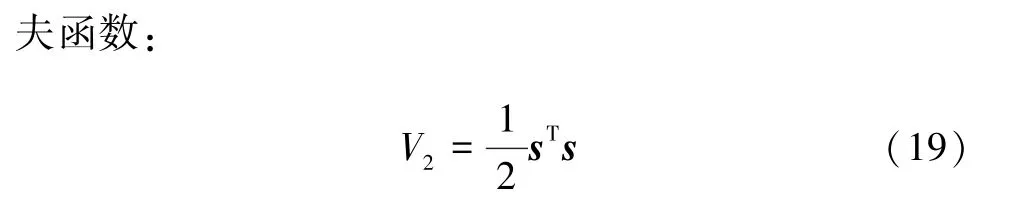
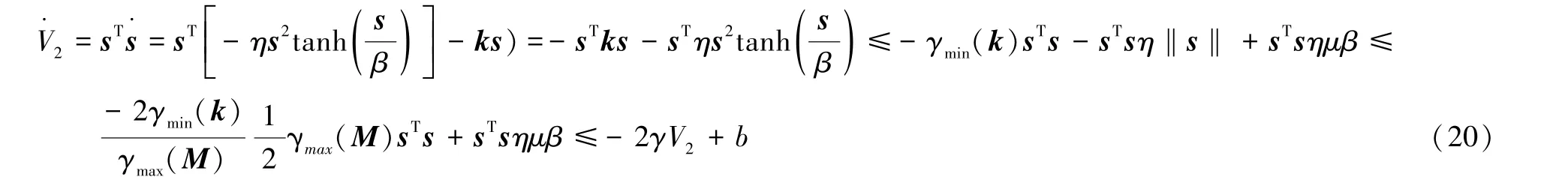
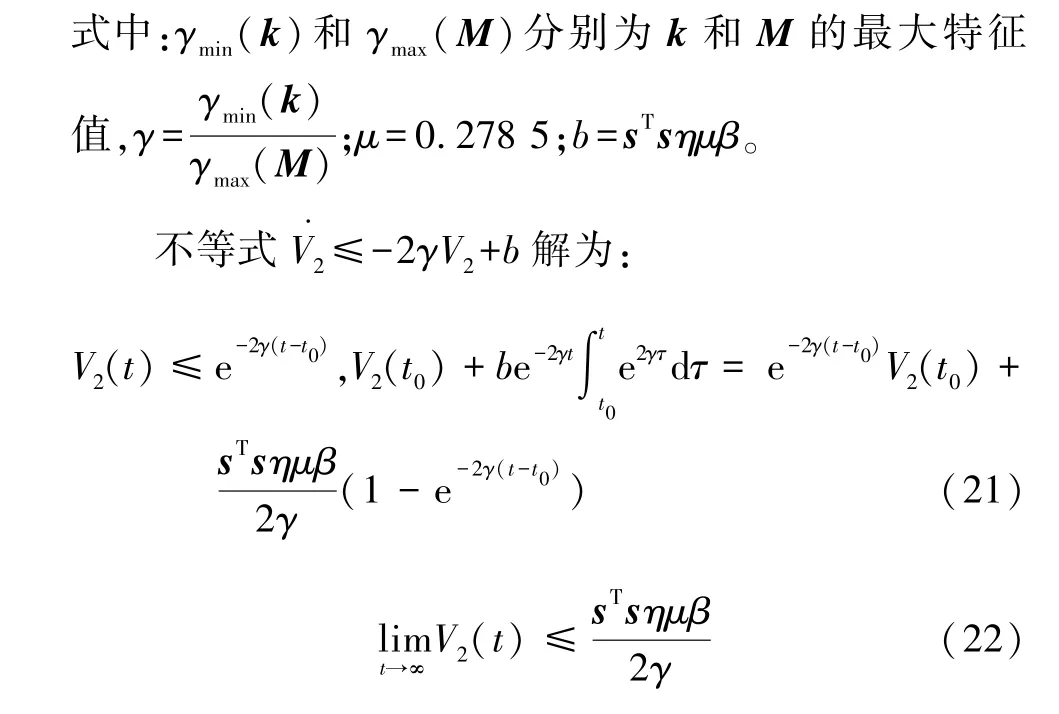
V2(t) 渐进收敛,收敛精度取决于sTsη、β和γ,sTsη不仅削弱了抖动的影响,还提高了系统的鲁棒性。

3 仿真验证

基于三连杆模型的下肢外骨骼机器人,对提出的控制策略进行仿真验证。 下肢外骨骼机器人参数如表1 所示。

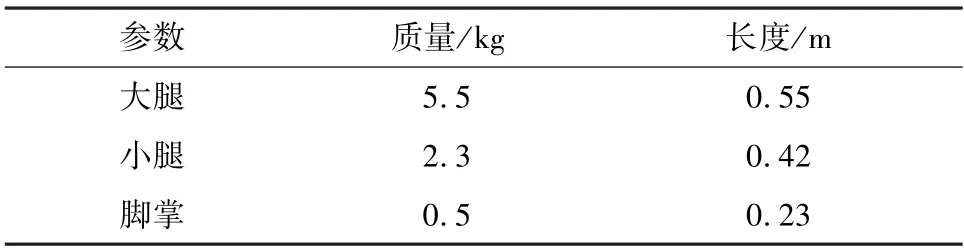
表1 下肢外骨骼机器人参数Tab.1 Parameters of lower limb exoskeleton robot

RBF 神经网络采用5 个输入单元、11 个中间单元、3 个输出单元的结构。 其中:b=10,c=0.2[-2.5-2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5]。 控制器的参数为:α=diag(20,10,10),λ=diag(300,100,100),β=0.01,η= 2,k= diag(300,300,300),关节的期望轨迹为:

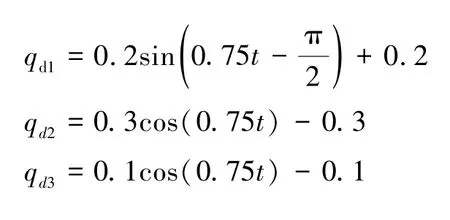
对改进前趋近律设计的控制率进行仿真。 改进前各关节的控制力矩如图3 所示。 由图3 可知,各关节控制器的输出会产生抖振,尤其是踝关节的控制输出抖振较大,这会影响下肢外骨骼机器人行走的稳定性。

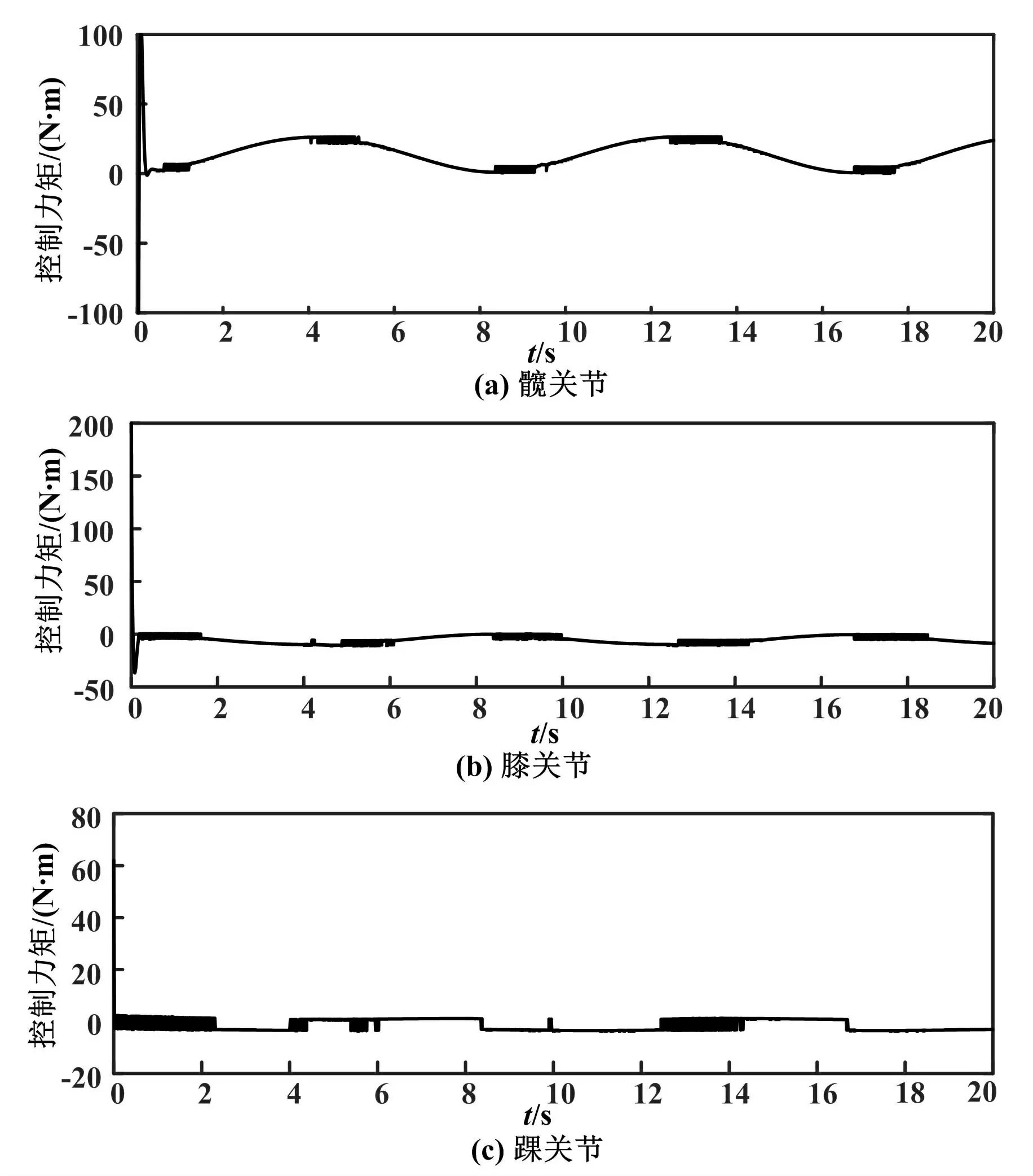
图3 改进前各关节的控制力矩Fig.3 The control torque of each joint before improvement

为了改善系统的稳定性,采用改进后的控制率。各关节角度跟踪、角速度跟踪和改进后各关节的控制力矩分别如图4、图5 和图6 所示。

图4 各关节角度跟踪Fig.4 Tracking the angle of each joint

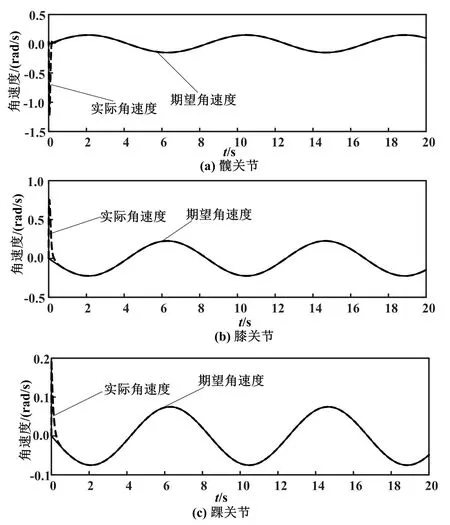
图5 各关节角速度跟踪Fig.5 Angular velocity tracking of each joint

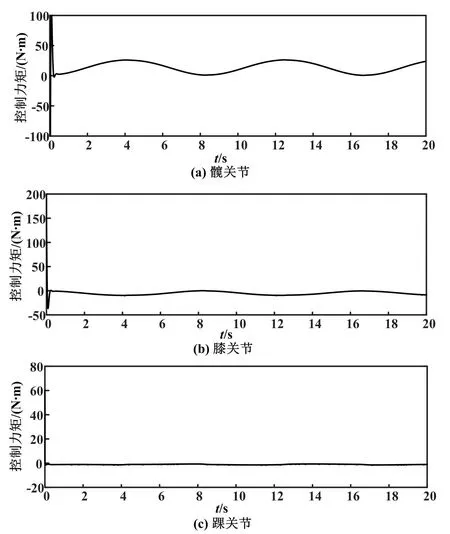
图6 改进后各关节的控制力矩Fig.6 The control torque of each joint after improvement

由图4、图5 和图6 可以看出,在考虑关节摩擦和环境扰动等不确定因素时,由于神经网络的自适应控制的调整,实际轨迹可以快速地跟踪期望轨迹,达到较为理想的跟踪效果。 通过改进的趋近律,控制器的输出抖振减弱,变得比较平滑。

为了验证神经网络自适应滑模控制的效果,将基于计算力矩法的滑模控制作为对比,控制器参数与神经网络滑模控制器参数相同,都采用改进的趋近律来减弱控制输入的抖动。 各关节角度跟踪误差如图7 所示。 基于计算力矩法的滑模控制跟踪误差有突刺,说明摩擦干扰对跟踪有一定影响。 而神经网络滑模控制误差曲线比较平滑,受摩擦干扰影响较小。

图7 各关节角度跟踪误差Fig.7 Angle tracking error of each joint

表2 为两种控制方法下,三个关节的跟踪误差对比。 由表2 可知,在改进趋近律下,基于神经网络的自适应滑模控制要比基于计算力矩法滑模控制的跟踪效果更好。

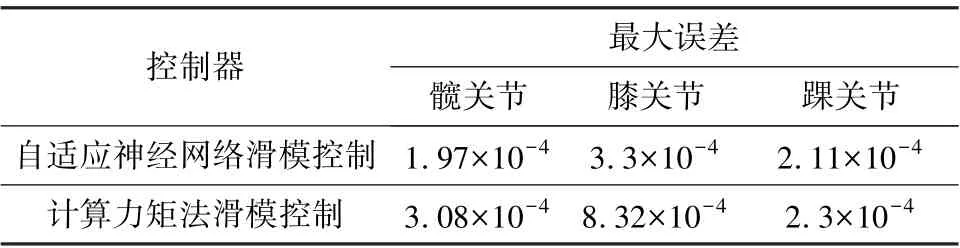
表2 三个关节的角度跟踪误差对比Tab.2 Comparison of angle tracking errors of three joints rad

4 结论

本文通过拉格朗日法建立了下肢外骨骼机器人的三连杆动力学模型。 针对其行走稳定性,引入RBF 神经网络逼近模型不确定项,对传统趋近律作了改进,并设计了基于改进趋近律的神经网络自适应滑模控制器。 通过对比仿真验证,并设计的控制器能实现期望轨迹的跟踪,改进的趋近律能有效地降低传统趋近律带来的抖振问题。 通过与改进趋近律下的基于计算力矩法的滑模控制作对比,证明了自适应神经网络滑模控制的跟踪效果更好。