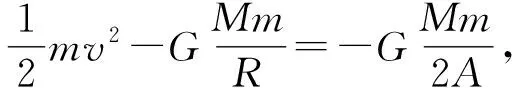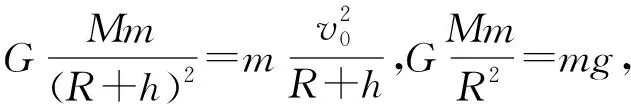离心率的物理意义及其应用

陆栋梁

(上海交通大学附属中学，上海 200439)

物理学中利用极坐标可描述天体运动的轨道，为某些问题的解决带来了便利。在极坐标中描述圆锥曲线要用到离心率的概念，在数学中离心率已有完善的定义，笔者试图寻找离心率的物理意义及其可能的应用。

1 数学中的离心率

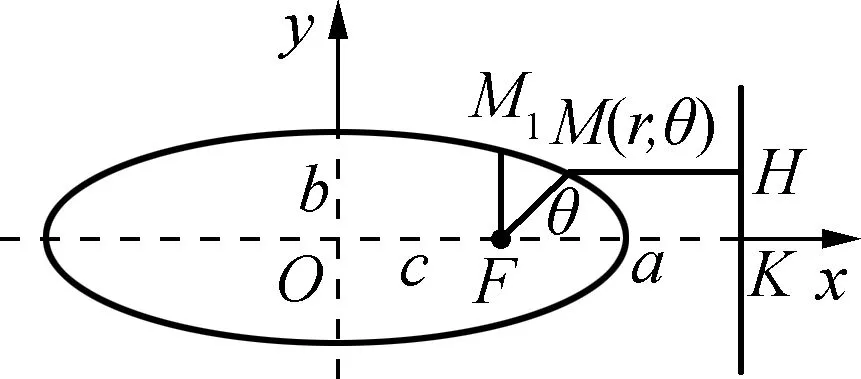
图1

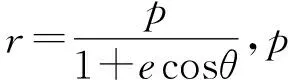
由解析几何知识可知，与椭圆同为圆锥曲线的抛物线和双曲线，其极坐标方程具有上述相同的形式，区别是抛物线的离心率e=1，而双曲线的离心率e>1。

2 霍曼转移

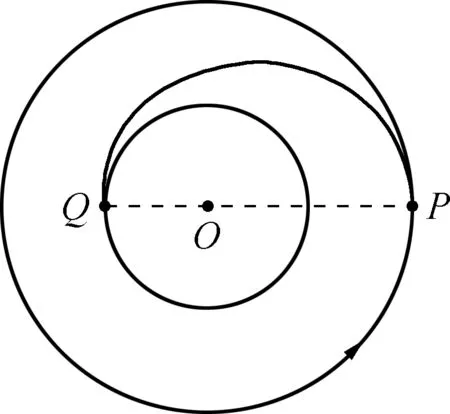
霍曼转移是一种将航天器从低圆轨道送往高圆轨道的方法。如图2所示，航天器在低圆轨道上沿原方向瞬间加速后，进入一个椭圆形的转移轨道(称为霍曼轨道)，抵达远拱点后再瞬间加速，进入高圆轨道，此即为目标轨道。这种转移方式消耗的能量最少，但耗时较长。

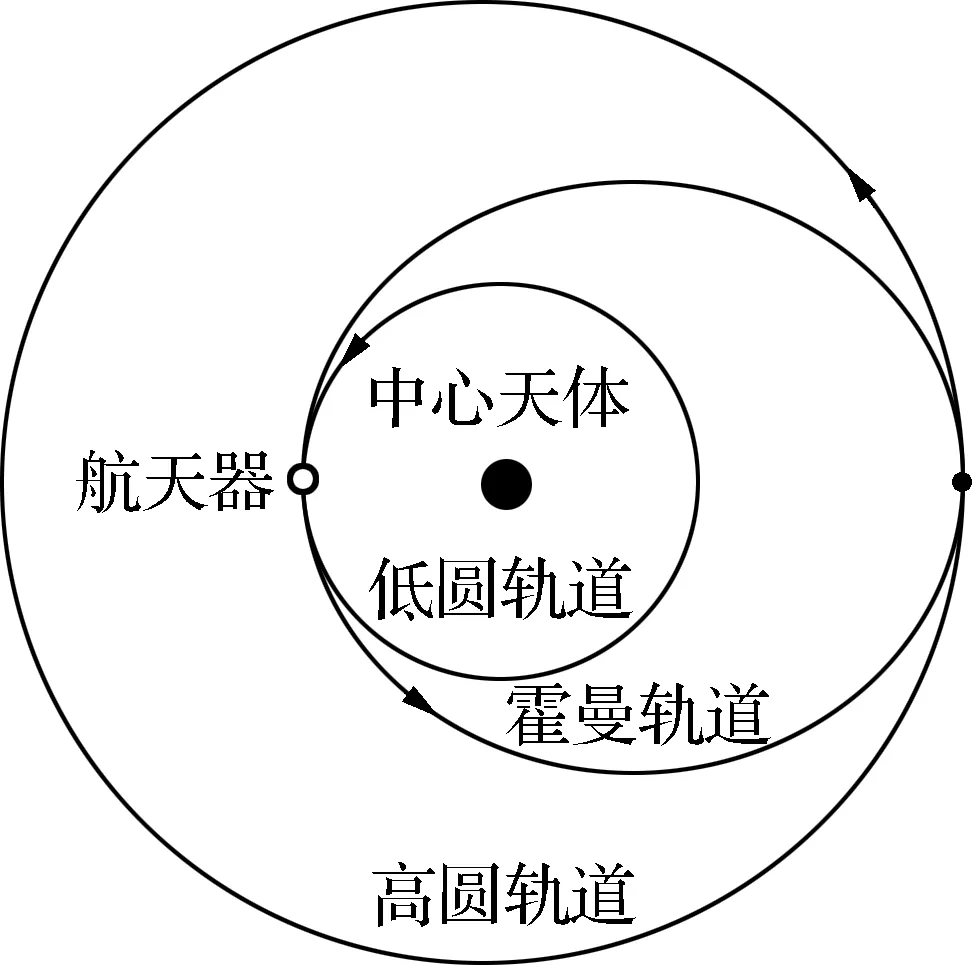
图2

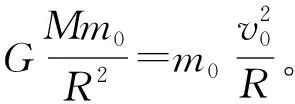
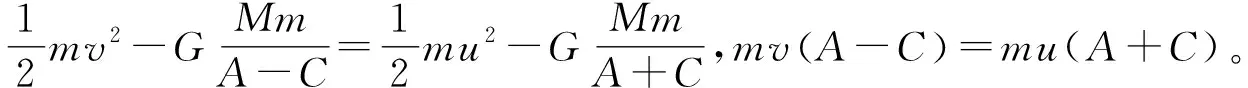
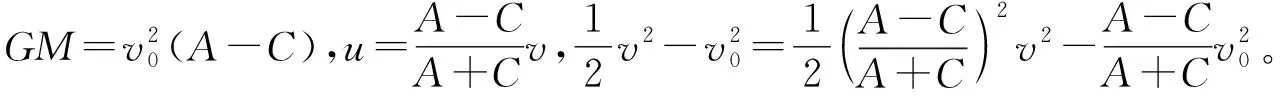
3 离心率的物理意义

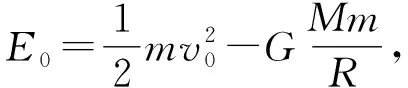
当航天器沿原有速度方向瞬时加速进入霍曼轨道时，会出现以下结果：

(1)若0<ΔEk

(2)若ΔEk=Ek0时，E=0，轨道为抛物线，此时e=1；

(3)当ΔEk>Ek0时，E>0，轨道为双曲线，此时e>1。

4 应用

另外，在霍曼转移问题中，若已知两个圆的轨道半径，通过离心率-能量关系式，可以计算航天器变轨所需的速度变化量，以下用例题予以说明。

图3

例：一质量为m的太空飞船在围绕月球的圆轨道上运动,其高度h=100km。为使飞船降落到月球表面,喷气发动机在P点作一次短时间发动。月球半径为R=1700km,月球表面的重力加速度g=1.7m/s2。如图3所示，若发动机向前喷射,使飞船到达月球背面的Q点，并相切，Q点与P点相对，求发动机喷射后的飞船速度大小。