高海拔地区三角堰流量系数测定试验研究*
2021-09-08次吉拉姆贾蒲云齐藤岳罗红英
次吉拉姆,贾蒲云,齐藤岳,罗红英
(西藏农牧学院 水利土木工程学院,西藏 林芝 860000)
西藏自治区位于青藏高原西南部,与印度等多个国家相邻。受地理条件的限制,西藏地区的经济一直处于较为落后的水平,但与其它省份相比较,西藏地区蕴藏着丰富的各类资源,尤其是水资源[1-2]。根据《中华人民共和国水法》中的法律条文规定,国家厉行节约用水,大力推行节约用水措施,发展节水经济型农业,建立节水经济型社会,而所有这些都得必须以实行节水的计量、有效提高水资源的使用为前提。精确的水量计算可以为灌区用水提供科学依据,能实现水资源的高效利用,提高灌区的科学化管理水平。
在水利水电工程的运行管理中,对薄壁堰的水力特性分析主要包括判别水流过闸的形式、流态以及流量的计算,若是对堰出流的水力特性分析解决不好,将会影响水利建筑物的正常运行,甚至会危及到上游地区人民的生命和财产安全[3-5],这种分析不仅对闸堰的水力计算理论具有一定的实际应用价值,而且对国民经济的发展、工程设计及应用方面具有重要的意义。对于堰出流的流量计算分析涉及两个方面的问题:一是堰出流流态的判别问题[6-7],二是堰出流综合流量系数的确定问题[7-11]。关于这方面国内外许多学者作了深入研究,其中不乏一些具有很高理论价值的研究思想,但是这些研究大多数仅仅局限于某个工程的研究,并没有形成统一的理论体系,并且有些理论概念模糊不清,所以大部分研究的成果不具有通用性,往往只是特例。
因此,本研究结合上述不足,以标准直角三角形薄壁堰为研究对象,以多功能水力试验平台——变坡型玻璃水槽为载体,系统研究不同流量下堰上水头值的变化规律,旨在得到适用于海拔3000m地区三角形薄壁堰的流量公式,对三角形薄壁堰流量公式系数进行修正,以对三角形薄壁堰流量公式计算体系予以补充和完善,与此同时对高原环境下三角形薄壁堰水力特性研究提供理论依据和指导作用。
1 三角型薄壁堰模型试验
1.1 试验模型
如图1所示,水槽长度为30m,净宽1m,净高0.7m。承重结构采用250mm×150mm×12mm的矩型钢管作为主梁支撑,主梁之间用同规格的钢管焊接;水槽玻璃安装均采用厚度为12mm钢化玻璃,有利于实验过程中直接读取数据,为实验的进行节约时间。三角型薄壁堰垂直于水流方向的缺口角度为90°,薄壁堰的尺寸:堰宽990mm、堰高500mm、堰口至堰顶的高度为335mm。堰型尺寸是根据水槽的尺寸所设计的,三角堰与水槽之间采用1mm厚的玻璃胶粘固。堰身采用不锈钢制作,可以有效承受水流的冲击力。堰口边缘处进行打磨,有利于水流从堰口射出。

图1 三角型薄壁堰模型图
1.2 试验原理
流通顺畅的玻璃水槽内流量越大,液位就越高;流量越小,液位就越低。通过测量出来的水位计算出过堰流量。普通明渠内流量与水位之间的对应关系,受渠道的坡降比和表面的糙度影响。若在玻璃水槽内安装量水堰,会产生节流作用,使渠道内的流量与液位有固定的对应关系。在本次试验过程中通过使用流量控制系统(DCMS)来设定目标流量,待实际流量值等于目标流量值之后,使用LS300-A形便携式流速测算仪来测试三个预测点的断面流速、使用水位测针测量堰上水头、使用粒子成像测速系统(PIV)得出速度场云图,最终得出流量与堰上水头之间的函数关系。
1.3 试验分析
所测堰上水头数据处理与分析,与所测断面流速数据处理与分析的方法相同,通过计算相对误差的方法对所测堰上水头值进行分析与处理。最终计算得到的误差分析数据见表1。
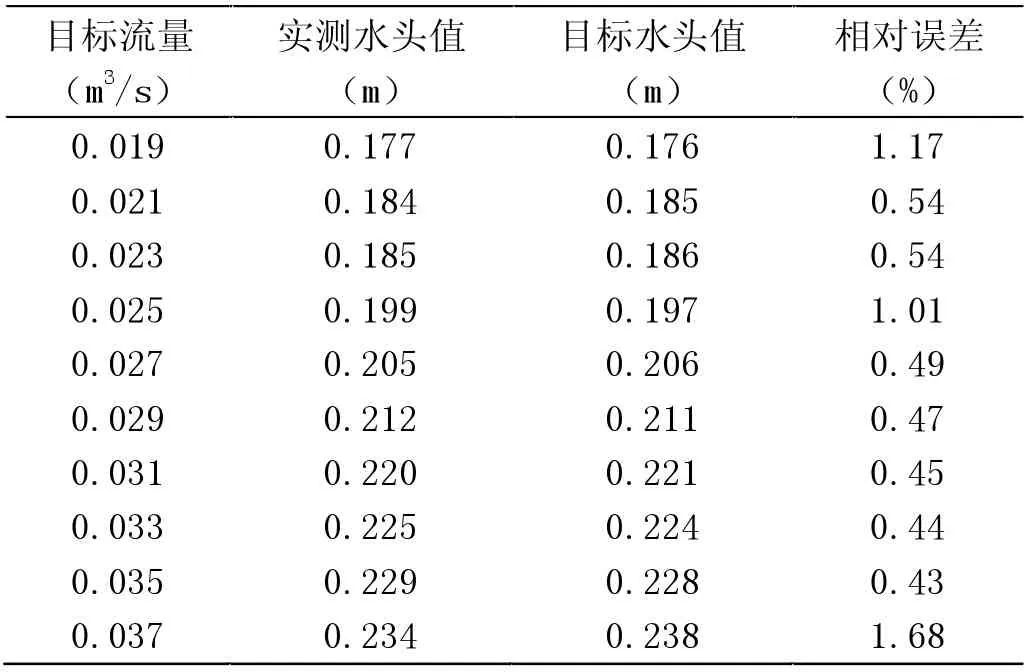
表1 水头值数据误差分析表
由水头值数据误差分析表可知,实测水头值与目标水头值之间的最大相对误差没超过5%,说明实验所测水头值可以使用。最终试验所测水头值数据见表2。
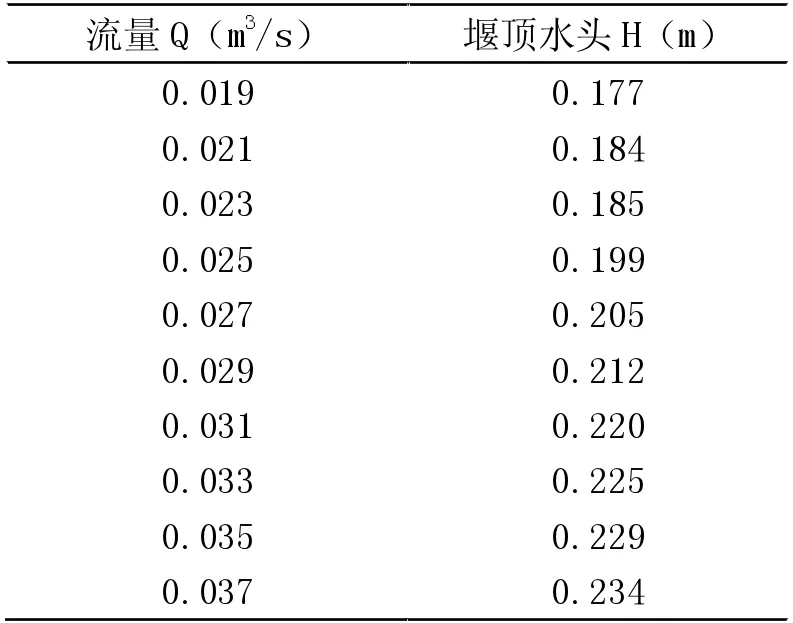
表2 不同工况下堰顶水头值数据
2 直接拟合流量公式
2.1 三角堰流量公式推导
经过上一节数据处理与对比分析,验证了试验所测数据的准确性。从以前的研究中可以发现标准直角三角堰过堰流量Q与堰上水头H之间存在函数关系,而且经总结共有三个经验公式分别为
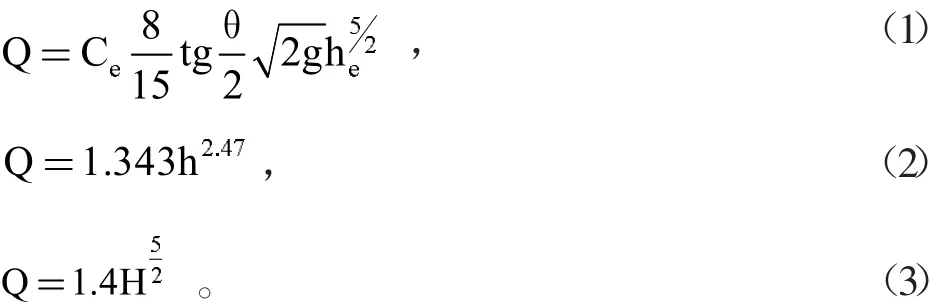
但是这三个经验公式都是在平原地区推导出来的,对于在高海拔地区所做的本次试验,这些公式的中流量系数是否仍为原值,我们不能确定,所以我们用通过试验所测的流量和堰上水头值来反向推导流量系数。
对公式:

两边取对数,则:

令:

则变成直线函数:

根据直线拟合公式:

由于x,y分别是水头、流量的对数值,所以在进行上式的计算时,必须先计算出xi,Σxiyi,Σyi的值。最终曲线拟合数据计算见表3。

表3 曲线拟合数据计算表
把表中的计算值对应代入上面式(8)、(9)求解得式(10)、(11):

得a=0.3508741315441,t=2.5,由于a=InC,得C=1.420,所以通过使用本次试验数据拟合出来的三角形薄壁堰的流量公式为:

注意式中的单位:流量Q为L/S,水头H为m。
2.2 拟合公式误差分析
用最小二乘法拟合出来的三角形薄壁堰的流量公式Q=1.420H2.5的拟合效果是好是坏我们不能确定,但是可以用残差来衡量,残差的平方和越小说明拟合效果越好。设Qi为实测流量,Qi’为用公式求出的流量,则ei=(Qi-Qi’)称为残差,残差的平方和(Σei2)的大小是衡量公式拟合好坏的重要标志,当然(Σei2)越小越好。具体残值求解数据计算见表4。
由表4可知Σ(ei2)=0.00000118,残差平方和很小,所以曲线拟合效果很好。

表4 残值求解数据计算表
2.3 相关性分析
通过计算残差的方法来验证曲线拟合效果的好坏,这样的验证方法太过单一,下面我们通过计算相关系数r来再次验证拟合公式的精确度。
计算相关系数r

式中:

令x0=xi-x,y0=yi-y,则公式(13)可变为:

把表中的相关数据带入公式(16)中:
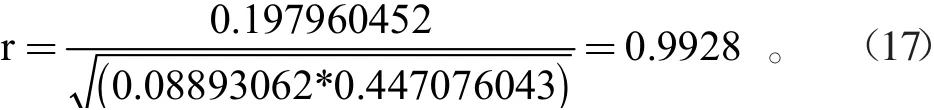
求出的相关系数r=0.9928已非常接近1,说明用最小二乘法拟合出的流量公式很好,出错的概率很小,即实测的水头——流量的点(Hi,Qi)几乎全部落在曲线Q=1.420H2.5上。查相关系数显著性检查表,当N=10,α=0.001时满足要求的相关系数r=0.823,我们计算出来的相关系数r=0.9928,远大于0.823,说明拟合的公式精度很高。最终相关系数计算表由表5所示。
2.4 两种流量公式量水精度对比
表6给出了采用以上两种流量公式计算流量与实测流量的对比,从表中可以看出,用公式(2)、(3)计算过堰流量与实际流量的最大误差是3.18%,最小误差是0.01%,平均误差为1.35%。利用直接拟合流量公式(12)计算出的流量与实际流量的最大误差3.75%,最小误差0.56,平均误差为1.71%。最终相对误差计算数据见表6。
由图2可看出,理论流量公式和拟合流量公式的精度都比较高,公式(2)、(3)测流误差均分布在5%的误差线以内;公式(12)直接拟合流量公式相对误差也在5%以内;这两种公式误差均在明渠测流要求误差内。因此,流量公式的使用应在实际应用中按需要进行选择。
3 流量系数的计算
高实用堰的研究比较成熟,流量系数的计算比较稳定;低实用堰的流量系数,因其影响因素较多,计算比较复杂。
根据《水力计算手册》[12]第二版,三角形薄壁堰流量计算公式:

式中:Q为过堰流量;Ce为流量系数;he为有效堰顶水头,he=h+Kh,h为实测堰顶水头,Kh为水头修正值,取值为0.00085m;θ为三角形缺口夹角。运用该式所限定的三个条件:θ=90°,模形试验完全符合。因此,本试验中该公式仍然使用,将试验数据带入上述公式可以得到不同堰高水头下测定的流量系数,具体数值见表7。
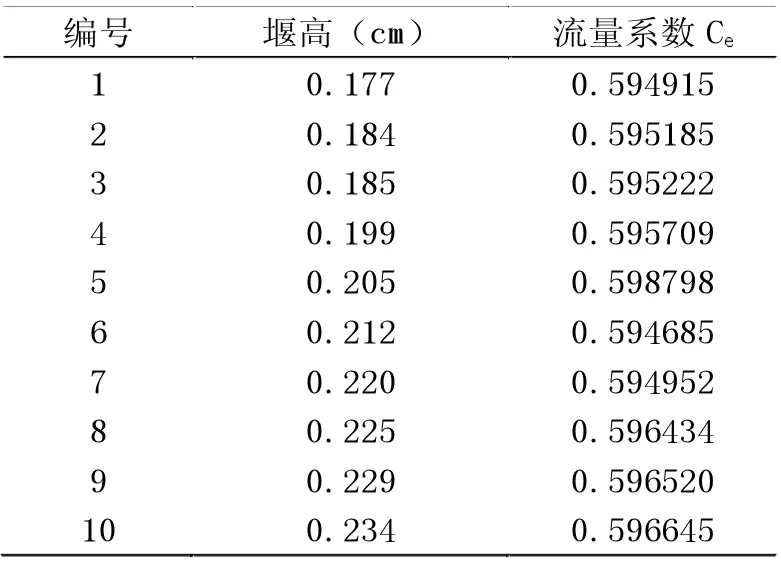
表7 不同堰高水头下的流量系数计算表
如图3,当堰高位于0.177-0.205m时,流量系数随堰高的增大而增大;当堰高位于0.205-0.212m时,流量系数随堰高的增大而减小;当堰高位于0.212-0.234m时,流量系数又随堰高的增大而增大。当堰高等于0.205m时,流量系数为最大值;当堰高等于0.212m时,流量系数为最小值。
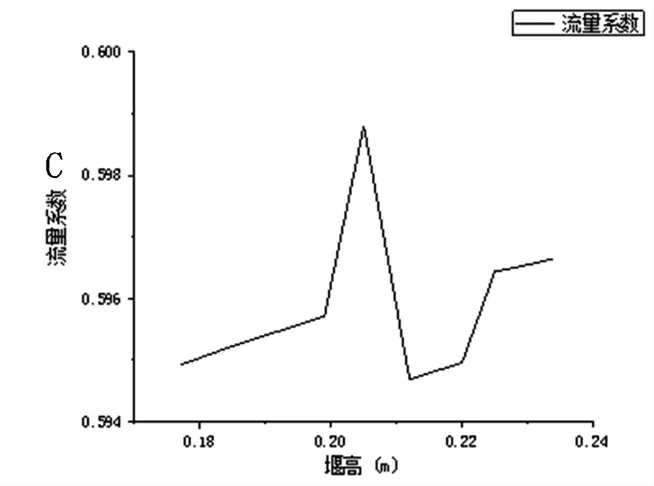
图3 流量系数随堰高变化曲线图
4 结论
本文通过理论分析得出自由出流状态下,三角形薄壁堰过堰流量系数的经验式。其中,这种流量公式都是基于上游水深的函数,因为在实际测量水流时,仅知堰前上游水深,通过试验得到结论如下:
(1)本文通过对原公式中的流量系数Ce用直接拟合方法,得出三角形薄壁堰过堰流量计算公式,结合数据处理过程中,得出三角形薄壁堰过堰流量与堰前水头和堰高间呈现较好的非线性关系,用直接拟合法得出流量公式经验式,相关系数较高,对于一般工程应用较为方便。
(2)根据数据分析计算出流量,通过经验公式和修正过的流量公式计算过堰流量,两种公式得到的流量基本相同。说明修正系数后的三角形薄壁堰流量公式对适当地量水堰的研究具有实际应用价值。
(3)通过理论公式直接拟合流量公式计算得到的相对误差都在5%以内,这两种公式误差均在明渠测流要求误差内。因此,流量公式的使用应在实际应用中按需要进行选择。
