起重船在抢险救援行动中的应用技术研究
2021-09-08周园园
周园园,邵 飞,高 岳
(陆军工程大学 野战工程学院,江苏 南京 210007)
在执行抢险救灾任务时,现有的舟桥器材虽然能够做到快速出动,但受作业条件限制,还不能在近海海域中得到应用。随着我国经济社会的发展,浮式工程结构在抢险救灾行动中受到广泛关注。
当前,国内外对浮式工程结构研究广泛。Kral和Kreuzer[1-2]对规则波浪中系泊起重船的运动进行了研究,将起重船视为由驳船和悬吊载荷组成的多刚体系统,给出动力学方程并进行了数值仿真和相轨迹分析。Ellerman等[3-4]在Kral工作的基础上,对同一起重船模型的非线性动力响应进行了详尽的试验与理论研究,主要关注分叉行为和吸引子的存在等非线性现象。Kreuzer和Wilke[5]在研究锚泊浮体的波浪动力响应时,应用线性势流理论计算浮体与波浪的相互作用,用改进的Morison公式计算锚链的水动力。沈庆等[6]给出了浮基多体系统自激运动响应的时域分析方法,考虑了多体系统内部的耦合以及浮基与流场的耦合,并根据多刚体动力学Huston方法建立了系统的动力学方程。Zhang等[7]介绍了海洋工程起重系统的发展和分类,对主要的近海起重船进行了分析,并给出了海洋工程起重系统优先研究方向和起重过程模拟的基本思路。
1 波浪基本理论
1.1 波浪的运动特性
波浪理论是揭示水波运动的内在本质,如波浪场中的水质点速度分布和压力分布等。对于波浪作用的研究一般从两个领域进行,一是从流体力学的角度,研究液体内部各质点的运动状态,包括线性波浪理论和非线性波浪理论[8];二是将海面波动看作是一个随机过程,揭示海浪内部波动能量的分布特性,从统计意义上对液体内部各质点的运动状态进行描述。水质点做振荡运动时,波形的推进运动如图1所示。

图1 波形的推进运动
建立简单波理论时,假定:流体是无黏性的理想流体,自由水面的压力是均匀的且为常数,水流运动时无旋;海底水平、不透水;流体上的质量力仅为重力,表面张力和柯氏力可忽略不计;波浪属于平面运动,即在x-z平面内做二维运动。
根据流体力学原理,在上述假定下的波浪运动为势运动,这种波浪称为势波。其水质点的水平速度u和垂直速度w可由速度势函数φ=(x,y,t)导出,即:

由流体的连续性方程:

将二式联立可得势波运动的控制方程,即拉普拉斯(Laplace)方程:

求解上述方程,需要确定边界条件,二维波动满足的边界条件包括以下三种。
(1)在海底表面,水质点垂直速度应为零,即:

(2)在波面z=η处,满足动力边界条件,分别为:

(3)上、下两端边界条件。
从空间和时间上看,同一相位点上的波要素值是相同的,可以写成:

式中,L、T分别为波浪的波长和周期。
1.2 质点运动轨迹
由以上假定可知,式(5)、(6)中的非线性项与线性项的比值是小量,可以忽略,方程中保留线性项。简化后可分别表示为:

二式联立可得:

对方程采用分离变量法,并利用边界条件,可得到势函数φ的解为:
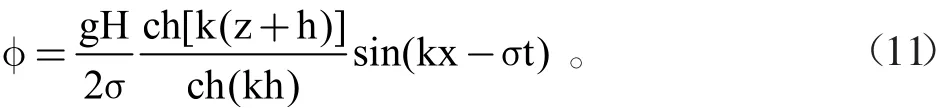
此时,自由水波面曲线式(9)可得:

根据势流理论,由式(12)可得流体内部任一点(x,z)处水质点运动的水平速度u和垂直速度w分别为:
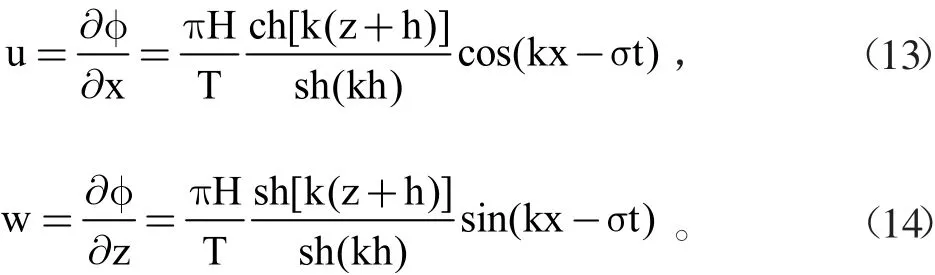
假定水质点的运动速度都等于流场中(x0,z0)处的速度,将流速对时间t进行积分就可以得到水质点的迁移量:
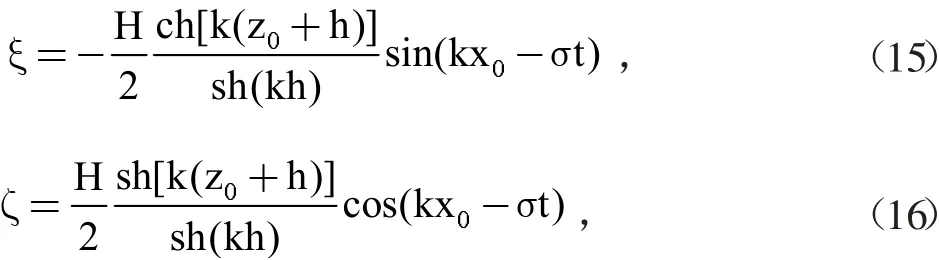
得到水质点运动轨迹方程:

此轨迹为一封闭椭圆,水面处b=H/2,即为波浪的振幅。
1.3 微幅波的压力场
根据线性化后的伯努力方程,可求波压力的表达式:

将势函数表达式代入,则有:

浅水情况下压力表达式可以简化为:

由上可以看出,浅水波的动水压力沿水深是一个常数,它不会随质点位置变化而改变。
2 起重船试验模型建立及分析
2.1 建立起重船试验模型
建立由趸船、配重、吊臂、荷载组成的起重船多刚体系统力学模型[9],如图2所示。趸船作为基座,一般为箱型结构[10]。取惯性坐标系o-xyz的原点与浮船静止时的质心重合,x轴指向船首,y轴指向左舷,z轴竖直向上。配重和吊臂可作为一个整体在水平面内绕z轴回转。吊臂与水平面的夹角称为吊臂的仰角,用φ表示。荷载用钢丝绳系于吊臂上端悬吊点。为便于计算转动惯量,各部件形状均取为规则的长方体。
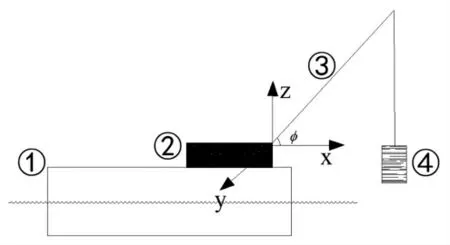
图2 起重船模型示意图
由趸船的横向尺寸(见表1),考虑附加转动惯量并参照试验数据资料[9],求得浮船横摇摆的固有周期T=1.55s,横摇阻尼比为0.05s。海况为三级波浪,波长40m,波高0.5m,周期T=5.06s,最大波面角α0=2.25°。上部机构(配重、吊臂和载荷)的质量与转动惯量远小于趸船(见表1),忽略上部机构运动趸船横摇运动的影响,并假定趸船的横摇轴通过质心,横摇固有频率远离波浪的激励频率,阻尼又较小,忽略阻尼对强迫横摇运动幅值的影响。根据船舶在波浪中无阻尼横摇的运动理论[11-12],趸船在三级波浪作用下的横摇角幅值θb方程为:


表1 起重船各部件的质量及尺寸参数
2.2 试验数据分析
2.2.1 吊臂夹角对趸船横摇的影响[13]
工况1-1:波长30m,波高0.4m(图3)。
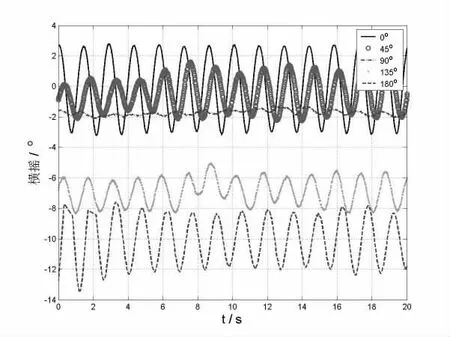
图3 30m波长,0.4m波高
工况1-2:波长40m,波高0.6m(图4)。

图4 40m波长,0.6m波高
结论1:30m波长、0.4m波高、0°角的摇摆幅度最大,频率跳动较快,对趸船的影响大,90°角方向上的摆动幅度最小,对趸船的影响较小,基本平稳;40m波长、0.6m波高、0°角的摇摆幅度最大,频率跳动较快,对趸船的影响大,90°角方向上的摆动幅度最小,对趸船的影响较小,基本平稳。
2.2.2 不同波长和波高对趸船横摇的影响[14]
工况2-1:吊臂夹角为0°(图5)。

图5 吊臂夹角为0°
工况2-2:吊臂夹角为45°(图6)。

图6 吊臂夹角为45°
工况2-3:吊臂夹角为90°(图7)。

图7 吊臂夹角为90°
工况2-4:吊臂夹角为135°(图8)。
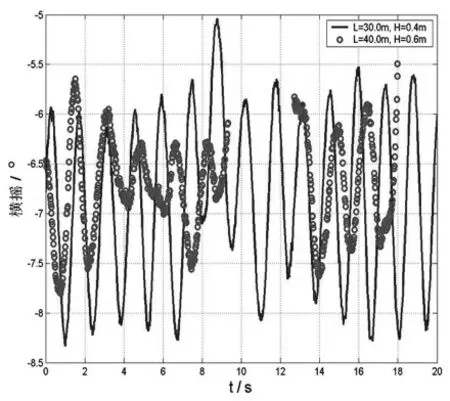
图8 吊臂夹角为135°
工况2-5:吊臂夹角为180°(图9)
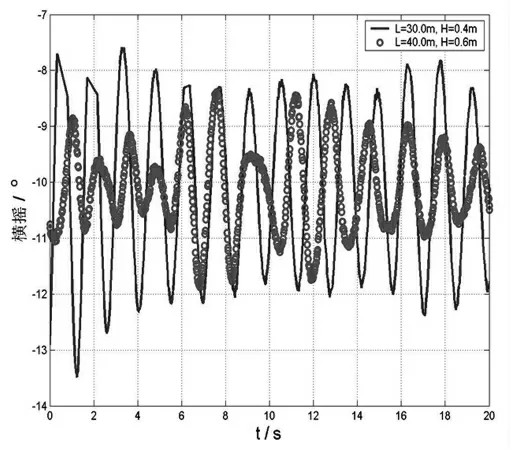
图9 吊臂夹角为180°
结论2:不论吊臂夹角为0°、45°、90°、135°、180°,波长越短,波高越低对趸船的影响越大,频率跳动越快,横摇摆幅度越不平稳。
2.2.3 夹角对重物运动范围的影响
工况3-1:波长30m,波高0.4m(图10)。
图10 波长30m,波高0.4m
工况3-2:波长40m,波高0.6m(图11)。

图11 波长40m,波高0.6m
结论3:30m波长、0.4m波高、0°角对重物的影响较大,晃动幅度最大,180°角对趸船的影响最小,晃动幅度最小,趸船最平稳;40m波长、0.6m波高、0°角对重物的影响较大,晃动幅度最大,180°角对趸船的影响最小,晃动幅度最小,趸船最平稳。
2.2.4 重物对趸船横摇和纵摇耦合运动的影响[15]
工况4-1:波长30m,波高0.4m,吊臂夹角0°(图12)。

图12
工况4-2:波长30m,波高0.4m,吊臂夹角45°(图13)。

图13
工况4-3:波长30m,波高0.4m,吊臂夹角90°(图14)。
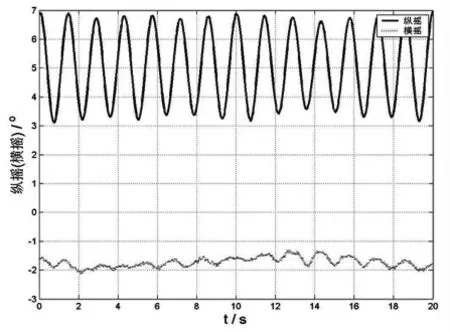
图14
工况4-4:波长30m,波高0.4m,吊臂夹角135°(图15)。

图15
工况4-5:波长30m,波高0.4m,吊臂夹角180°(图16)。

图16
工况4-6:波长40m,波高0.6m,吊臂夹角0°(图17)。
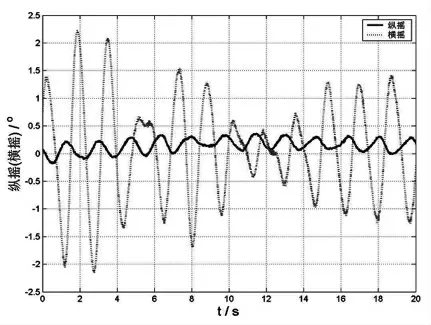
图17
工况4-7:波长40m,波高0.6m,吊臂夹角45°(图18)。

图18
工况4-8:波长40m,波高0.6m,吊臂夹角90°(图19)。

图19
工况4-9:波长40m,波高0.6m,吊臂夹角135°(图20)。
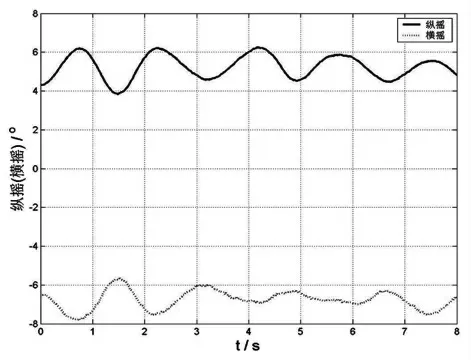
图20
工况4-10:波长40m,波高0.6m,吊臂夹角180°(图21)。

图21
结论4:(1)30m波长、0.4m波高,吊臂夹角为0°和180°对纵摇影响较大,吊臂夹角为90°对横摇影响较大,吊臂夹角为45°和135°对纵摇横摇影响都很大,频率跳动快,作业最不安全,尽量避免。
(2)40m波长、0.6m波高,吊臂夹角为0°和180°对纵摇影响大,吊臂夹角为90°和135°趸船晃动幅度大,吊臂夹角为45°,横摇、纵摇的晃动幅度都很大,频率较快,不利于安全作业,尽量避免。
3 结束语
浮式工程结构中,起重船在内河中应用广泛,但是尚未在执行近海抢险救援任务中得到有效应用,本文结合现行条件下舟桥装备无法在近海海域开展抢险救援行动,而起重船在地方上保有量大,机动性和适应性良好,作业效率高,研究利用起重船打捞作业应用技术,保障应急救援力量快速完成抢险救援任务。
