两种工程化的航天器用滚动轴承加速寿命试验方法
2021-09-08黄首清姚泽民张禹森黄小凯刘守文
黄首清,代 巍*,姚泽民,张禹森,黄小凯,刘守文
(1. 航天机电产品环境可靠性试验技术北京市重点实验室; 2. 北京卫星环境工程研究所:北京 100094)
0 引言
滚动轴承是航天器转动类产品的关键零部件,其在长期在轨运行过程中可能由于疲劳、磨损等原因出现性能退化(摩擦系数增加、回转精度降低等),影响相关产品乃至航天器整器的性能和可靠性,因此需要对其开展充分的寿命试验评估。而对于长寿命高可靠航天器用滚动轴承,传统的1∶1 寿命试验很难满足研制进度要求和经费限制,须开展加速寿命试验。
加速寿命试验是为缩短试验时间,在不改变故障机理和故障模式的前提下,用提高应力水平的方法进行的寿命试验[1]。徐东等[2]深入分析滚动轴承加速寿命试验过程中遇到的各种问题,提出一套较完整的滚动轴承加速寿命试验方法。李新立等[3]针对某航天器天线指向机构固体润滑球轴承,开展了恒定应力加速寿命试验方法研究。黄小凯等[4]建立基于响应面方法辨识不同应力与轴承失效响应值之间关系的加速模型,并进行了模型验证试验。基于加速寿命试验数据,可利用各种模型对滚动轴承的寿命与可靠性开展预测评估[5-7]。目前国内外已经制定了一些针对滚动轴承加速寿命试验设计和实施的标准,如ISO 281[8]、GB/T 24607[9]等,但是尚缺乏具备较强工程可操作性的加速寿命试验方法。
本文针对小子样场景下长寿命高可靠航天器用滚动轴承寿命快速试验评估的难题,提出两种工程化的加速寿命试验方法:方案1 为鉴定性试验,主要适用于疲劳失效模式以及小子样场景;方案2为摸底性试验,适用于各类失效模式。
1 试验方法
本部分主要介绍两种试验方案在加速应力、加速模型、样本数量及试验时间等关键要素上的选取思路及依据。
1.1 加速应力
滚动轴承的加速寿命试验中,可选择的加速应力包括转速、温度和当量动载荷。其中:温度可导致轴承润滑状态、摩擦状态及材料参数等发生复杂变化,难以准确地用加速模型来描述其加速效应,故不推荐其作为加速应力;若以转速作为加速应力,则属于时间压缩类加速试验,但高速轴承的加速空间有限,不在本文讨论范围内。因此,本文提出的两种试验方案均以当量动载荷Pr作为轴承加速寿命试验的加速应力,其计算公式为

式中:Fr和Fa分别为轴承的径向和轴向载荷;X、Y分别为径向和轴向载荷系数,这两个系数与接触角、轴向相对载荷系数有关,可通过GB/T 6391《滚动轴承 额定动载荷和额定寿命》[10]确定。在径向力保持不变的情况下,轴向力决定当量动载荷的大小,故为降低试验复杂度,取轴向力作为加速应力。
1.2 加速模型
加速模型是指寿命与应力之间的关系模型,本文涉及的两种试验方案采用不同的加速模型。
方案1 适用于小样本量且以疲劳失效为主的情况,因此基于疲劳寿命模型构建加速模型。轴承疲劳寿命的计算公式为
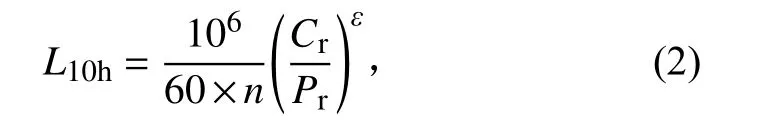
式中:L10h为基本额定寿命,h;n为工作转速;Cr为额定动载荷;ε为寿命指数,球轴承取ε=3。
在式(2)的基础上增加修正系数,可得

式中:a1为可靠性系数;a2为材料系数;a3为工作条件系数,主要包括润滑及温度条件。由于轴向力对式(3)的3 个系数均不产生影响,故计算加速应力时可将这3 个系数约去,则经过变换可求得滚动轴承加速寿命试验的加速系数为

式中:Lhi和Lhj分别为加速和正常状态下的轴承寿命;Pi和Pj分别为加速和正常状态下的当量动载荷。
方案2 对失效模式没有要求,仅须确保各加速应力与正常应力下的失效模式一致,适用于较多样本的情况。方案2 的加速模型根据GB/T 34986《产品加速试验方法》[11]选取,标准规定当试验加速应力为机械应力时,应采用逆幂律模型。该模型的特点是寿命随施加应力(负载)的n次幂的增大而减小,表达式为

式中:Ls为加速应力ωi下的平均寿命;C和n为待定系数。而正常应力下的平均寿命为

式中ω0为轴承实际运行过程中所受的应力。
为了方便进行参数估计,将逆幂律模型归一化处理为
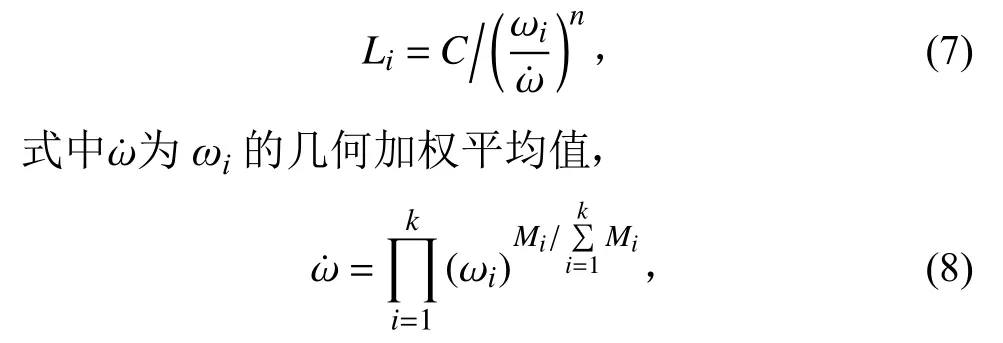
式中:k为应力水平的数量;Mi为第i种应力水平下的失效试验件数量。

试验过程中若有未发生失效的试验件,则可选择有退化趋势的故障判据测试参数,建立描述性能参数随时间变化规律的退化模型

其中β1,β2,β3,…,βj为各个退化性能参数。结合故障判据,可以推断出该应力下滚动轴承的伪寿命。将伪寿命值和试验直接测得的寿命值等效应用到加速模型参数估计公式中,可解决有效样本不足的问题。
1.3 样本数量及试验时间
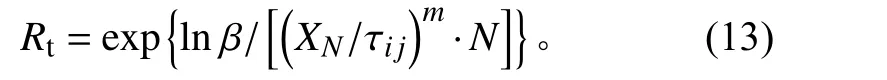
对于方案1,根据文献[12]可知,滚动轴承寿命末期可靠度指标下限值Rt、样本量N和1∶1 试验时间与寿命指标的比值XN符合以下关系式,式中:β为生产方风险系数;m为威布尔分布形状参数。在Rt、β和m确定的前提下,可根据该公式确定样本量N、加速系数τij及试验时间三者的关系。如加速应力(轴向力)越大,则加速系数越大,试验时间越短;但轴向力不可过大,以免引起其他失效模式;而且考虑成本等因素,试验时间不可过长,样本量不可过多,因此需要在三者之间权衡取舍。
方案2 的样本数量依据GB 2689.1《恒定应力寿命试验和加速寿命试验方法总则》[13]选取,标准中规定对于恒定应力加速寿命试验,每组应力水平下的试验件数量为至少5 个,而加速应力一般分为3~4 组应力水平,因此试验件样本量最低为15 个。在试验时间方面,方案2 为定数截尾和定时截尾相结合,即在达到规定的失效数(一般要求全部试验件均失效)或达到规定的试验时间(一般根据型号研制进度要求确定)后停止试验。完成全部试验后,应利用宏观分析、微观分析及化学检验等手段对失效样本进行必要的失效分析,确保各应力下失效样本的失效机理一致,不符合该条件的样本不得计入有效样本。
2 寿命与可靠性分析
方案1 为鉴定性试验,如果在试验截止时间前所有试验件均未失效,则表示所鉴定的滚动轴承满足给定的寿命和可靠度指标要求;而如果在试验截止时间前任一试验件出现失效,则认为所鉴定的滚动轴承不满足给定的寿命和可靠度指标要求。也就是说,方案1 仅可给出是否满足寿命下限值的定性结论。
方案2 为摸底性试验,基于滚动轴承的失效率可视为满足威布尔分布,其可靠度的表达式为

式中η为特征寿命参数,需要基于加速寿命试验数据进行计算。
首先计算正常应力下的寿命。可根据式(10),将应力水平ωi下任意第j个试验件的失效寿命Lij转换为正常应力ω0下的寿命L0ij,即

式中:k为加速应力水平数;Mi为每组加速应力水平下的失效试验件数量。对于失效数<3 的情况,可根据工程经验确定m。


根据上述思路,方案2 的寿命评估流程如图1所示。

图1 方案2 的寿命评估流程Fig. 1 Flow chart of life assessment of Scheme II
3 算例
以某型号航天器轴承组件为试验对象,介绍上述两种试验方法的具体算例。该航天器平台设计寿命16 年,而目前经过试验验证的轴承组件设计寿命只有5 年,因此需要针对轴承组件开展加速寿命试验研究,以获取其寿命指标和寿命末期可靠度指标。
3.1 方案1(鉴定性试验)
某型号航天器轴承组件的寿命技术要求为Rt=0.99、β=0.1,威布尔分布形状参数m保守取值为1.5。根据可靠度指标公式(13),可计算出在轴承组件正常运转下(即加速系数τij=1 时),样本量N与寿命试验时间的关系如表1 所示。

表1 样本量与寿命试验时间的关系Table 1 Relationship between sample size and life test time
从表1 中可以看出,试验样本量越多,需要的试验时间越短,但在不考虑应力加速的情况下,表中给出的试验时间都过于漫长,不具有可操作性。根据1.1 节的分析,需要以轴向力作为加速应力开展加速试验。
该轴承的设计当量动载荷为37.78 N,因此以50 N 作为最小施加应力;根据标准[9]中的要求,许用当量动载荷(与许用轴向力对应)为额定动载荷的20%~30%。该轴承所在单机产品研制技术要求其额定动载荷为6245 N,按20%计算则为6245×20%=1249 N,对应的许用轴向力为1 241.16 N。考虑到过大的轴向力可能改变失效机理,保守起见,取加速寿命试验中的最大轴向力为350 N,在100~350 N 之间等间隔取6 个轴向力进行加速试验。根据公式(1)并查询标准确定系数X和Y后,可得到当量动载荷与轴向力的对应关系如表2 所示。

表2 典型当量动载荷与轴向力对应关系Table 2 Relationship between typical equivalent dynamic load and axial force
基于该轴承的设计当量动载荷,根据公式(4)可确定加速系数与试验当量动载荷的关系,并结合表2 确定各轴向力下的加速系数,如表3 所示。

表3 各轴向力下的加速系数Table 3 Acceleration factor for different values of axial force
参考表1 中样本量与寿命时间之间的关系,可以得出不同样本量下对应的轴向力与无故障寿命试验时间的关系,如表4 所示。
在试验实施过程中,综合考虑可承受的试验时间、样本量及试验风险,参照表4 选择相应的样本量和加速试验应力水平,表中加粗的9 种样本量与轴向力组合可重点考虑作为验证滚动轴承16 年寿命技术要求的试验参数。
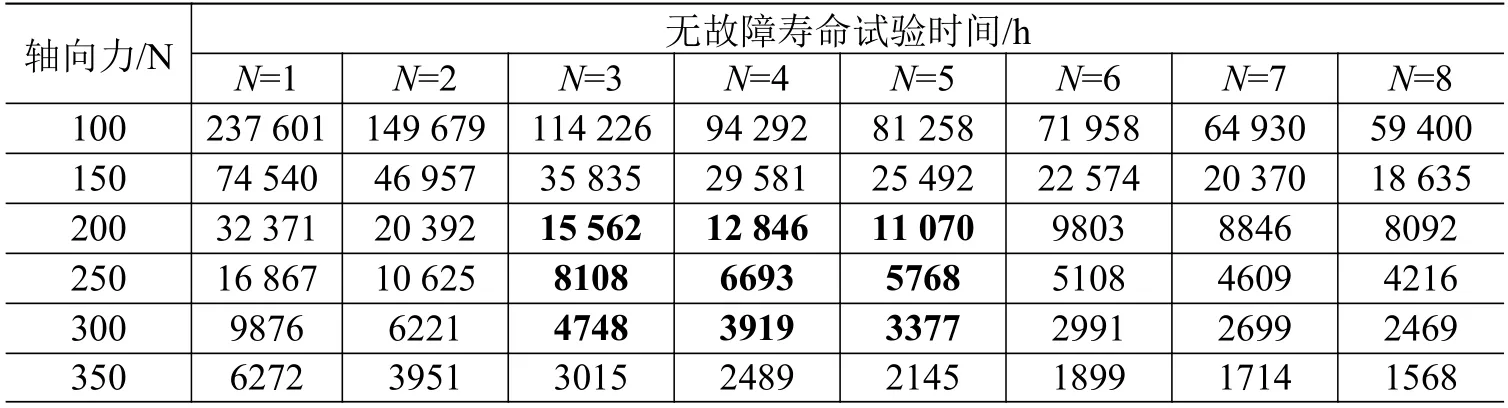
表4 不同样本量下对应的轴向力与无故障寿命试验时间的关系Table 4 Relationship between axial force and failure-free test time for different sample sizes
3.2 方案2(摸底性试验)
根据方案1 的分析与计算结果,以轴向力作为加速应力,其取值为200~300 N;滚动球轴承的失效模型满足逆幂律关系,因此其中间加速应力水平ωi(i= 3)可按照公式

在上述3 个应力水平下,各取5 个试验件开展加速寿命试验。综合考虑型号研制进度和试验结果可信度,取试验截止时间为12 960 h(约1.5 a),对达到试验截止时间仍未失效的轴承进行退化建模,将退化建模得到的伪寿命值作为该轴承的试验寿命。通过试验及外推得到的各试验件寿命如表5所示。
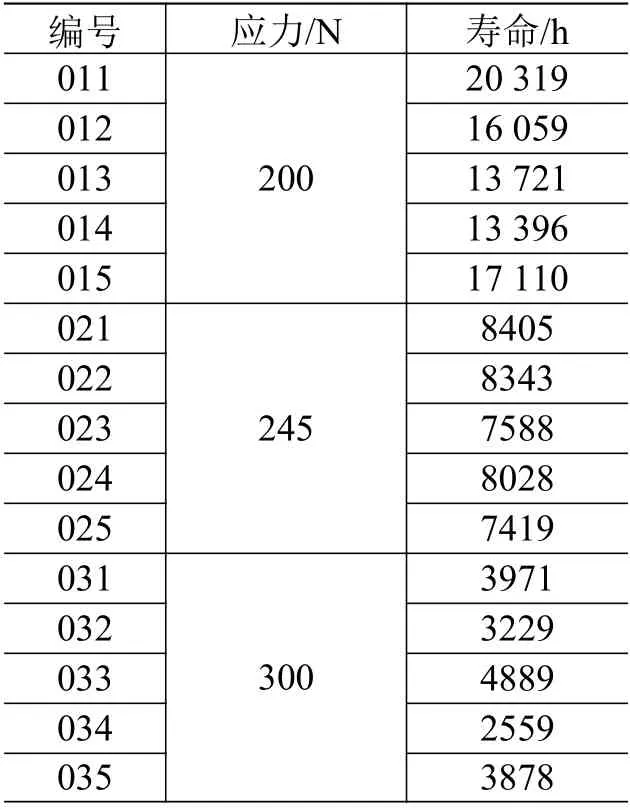
表5 各试验件应力水平及寿命Table 5 Stress levels and extrapolated life time for 15 samples
根据表5 给出的数据可知,各应力水平下的平均寿命估计值为Lˆ1=16 121 h、Lˆ2=7956 h、Lˆ3=3705 h。根据3 种应力水平下的寿命试验数据,对加速模型的参数进行估计并代入公式(9)可得:
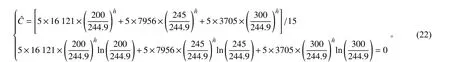


图2 f(m)函数曲线Fig. 2 Curve of function f(m)
通过比对,找出f(m)函数曲线与直线y=0 的交点,求得满足f(m)=0 的m值约为1.83。



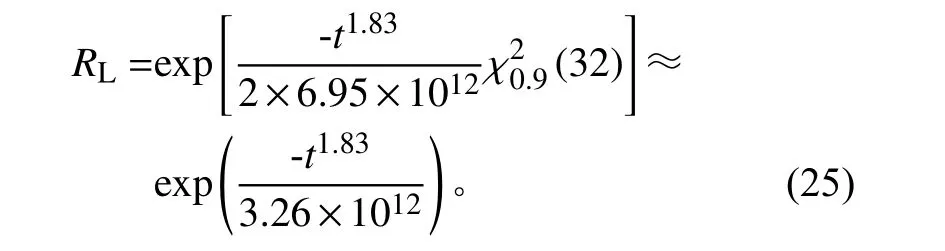
根据式(24)和式(25)的计算结果,绘制可靠度点估计值曲线和0.9 置信度的可靠度下限曲线,如图3 所示。
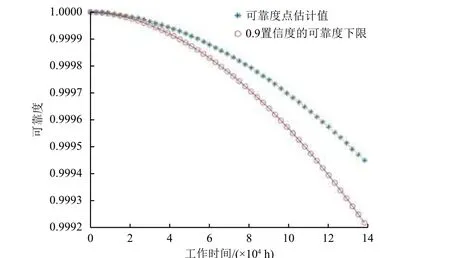
图3 可靠度点估计值和下限值与工作时间的关系Fig. 3 Point estimates and lower limits of reliability against working hours
从图3 可以看出,滚动轴承的可靠度随着工作时间的延长不断下降,在16 年寿命末期即1.4×105h的时间点,滚动轴承的可靠度点估计值和0.9 置信度的可靠度下限分别为0.999 5 和0.999 2。
3.3 对比分析
从以上两种试验方案的具体算例可以看出,方案1 需要的试验样本数为3~5 个,远小于方案2需要的15 个,且方案1 可以通过提高加速应力来压缩试验时间;同时,由于不涉及复杂的参数计算,方案1 的操作难度也更低。
但是,方案1 的试验结果仅能定性判断滚动轴承是否满足给定的寿命和可靠度指标要求,无法对其寿命和可靠度进行预估;而方案2 可通过参数估计加速模型和可靠性模型参数,提供更为丰富的结果,如滚动轴承的平均寿命、可靠度点估计值和下限值等,但相应的参数估计等计算过程较为复杂。
4 结论
本文提出针对航天器用滚动轴承的两种工程化的加速寿命试验方法,以解决小子样场景下长寿命高可靠航天器用滚动轴承寿命快速试验评估的难题;并基于某型号航天器用滚动轴承的具体案例,介绍了这两种试验方法的实施过程及特点,主要结论如下:
1)以某型号航天器用滚动轴承考核16 年寿命为例,方案1 需要的试验样本数为3~5 个,试验时间最短只需3377 h;方案2 需要的试验样本数为15 个,试验时间为12 960 h,成本显著高于方案1。
2)基于方案2 开展试验得到某型号航天器用滚动轴承在200、245、300 N 三种轴向应力水平下的平均寿命分别为16 121、7956、3705 h;通过参数估计和可靠度计算,得到该滚动轴承在16 年寿命末期的可靠度点估计值和0.9 置信度的可靠度下限分别为0.999 5 和0.999 2。
本文提出的两种试验方案将加速应力、加速模型、样本数量、试验时间及可靠性分析相结合,可作为操作性较强、适合工程应用的航天器用滚动轴承加速寿命试验解决方案。
