卫星气体工质剩余量高精度显式计算方法
2021-09-08宇文雷丁凤林李玉峰方忠坚
高 永,宇文雷,丁凤林,李玉峰,黎 明,方忠坚
(1. 北京控制工程研究所; 2. 北京市高效能及绿色宇航推进工程技术研究中心:北京 100190;3. 兰州空间技术物理研究所,兰州 730010; 4. 航天东方红卫星有限公司,北京 100094)
0 引言
冷气推进系统是指采用高压气体作为工质,经过系统减压后,由喷管加速喷出产生推力的一类推进系统。其优点是结构简单、性能稳定、安全可靠、成本低、功耗小、无毒无污染,缺点是比冲较低;随着化学推进和电推进等高比冲推进技术的发展,冷气推进系统逐渐被淘汰[1]。然而,随着重力类科学探测卫星和小型化微纳卫星的快速发展,冷气推进系统重新展现出其独有的优势,延伸出高精度冷气推进和微小型模块化冷气推进两个发展方向[2-3]。
面向重力类科学探测卫星应用的高精度冷气推进系统具有推力精度高和系统质心稳两大特点,其推力范围涵盖mN 至μN 的量级,推力精度相比传统冷气推进系统提高了3~6 个数量级[3-4]。但此类卫星的星上有效载荷对整星质心变化敏感,因此其推进系统的运动部件、气体质量均需要进行精确的控制和计算。其中冷气推进系统工质剩余量是推进系统的关键参数之一,其计算精度直接关系到卫星质量的计算精度,间接影响卫星科学数据的处理精度[5]。
冷气推进系统的工质多选用氮气、氙气等惰性气体,相对于其他惰性气体,氮气的有效比冲较高,故应用较多;系统的初始压力一般为15~30 MPa。工质剩余量的计算一般基于气体状态方程展开:鄢青青等[6]在姿控推进剂加注量的精确计算中,采用理想气体状态方程对增压气体质量进行评估,应用压力不超过0.2 MPa;李强等[7]对在轨冷气推进系统的泄漏估计中,同样基于理想气体状态方程对气体质量进行计算,应用压力不超过13 MPa;Zou 等[8]比较不同状态方程计算得到最高70 MPa 压力下的氢气密度,发现在高压下不同状态方程的计算结果出现明显差别;张涛等[9]对超高压冷气推进系统压力模块的性能开展数值研究,采用维里方程处理实际气体行为,应用压力最高120 MPa。
本文针对高压氮气冷气推进系统的工质剩余量计算问题,首先比较基于实际气体状态方程与基于数据库查询的气体密度计算误差,从中选取适合高压氮气密度计算的方法;然后提出一种显式计算方法,用于在判读卫星实时遥测数据期间快速获取气体工质剩余量;此外,对冷气推进系统中高压气瓶在不同压力下的容积变化进行量化评估,从而得到一种经过容积修正的高压冷气推进系统剩余量精确计算方法;最后通过两件气瓶的地面加注量试验,对该计算方法的适用性进行试验验证。
1 工质剩余量计算方法
1.1 冷气推进系统简介
冷气推进系统主要由高压气瓶、气加注阀、高压压力传感器、自锁阀、减压装置、低压压力传感器、缓冲气容、过滤器、推力器组件以及管路和连接件组成(参见图1)。

图1 典型冷气推进系统组成Fig. 1 Sketch of satellite cold gas propulsion system
冷气推进系统的加注一般在发射场进行。加注前,通过地面管路将地面气源与加注操作台连接,再通过气加注阀将气源接入推进系统的高压气瓶,组成一套密封系统;加注时,由加注操作台控制流入高压气瓶的气体流量,并实时监视气瓶的压力和温度;加注完成后,需将卫星静置10 h 以上,待气瓶处于平衡状态时测量得到气瓶真实的温度和压力值。气体加注量m的计算式为

其中:气体密度ρ根据监测所得气瓶温度和压力值利用气体状态方程计算或由数据库查询得到;气瓶容积V通过地面试验测得。
1.2 气体密度计算方法
当气体压力较低时,可近似认为其满足理想气体状态方程;当气体压力较高或者温度较低时,气体分子体积和气体分子间作用力不可忽略,真实气体效应明显。目前,描述气体压力、温度和密度的真实气体状态方程包括Van der Waals 方程、Redliche-Kwong(RK)方程和Peng-Robinson(PR)方程等。
理想气体状态方程为

式(2)~式(14)中:气体密度ρ(kg/m3)可由气体摩尔体积Vm(m3/mol)换算得到,ρ=M/Vm,M为气体分子质量,kg/mol;p为系统压力,Pa;T为系统温度,K;R为理想气体常数,8.314 J/(mol∙K);Tc为气体临界温度,K;Pc为气体临界压力,Pa;ω为偏心系数。
除了采用气体状态方程求解外,工程上多采用曲线图、表格或者数据库来表达和查询气体密度与温度和压力的关系。如美国国家标准与技术研究院(NIST)数据库即提供各类气体的化学和物理性质参数。该数据库来自文献数据的长期收集和积累,是一个非常实用的数据库。图2 给出NIST 数据库中的氮气密度-压力-温度关系曲面(253~333 K,0~30 MPa),密度的计算精度达到0.02%[13]。
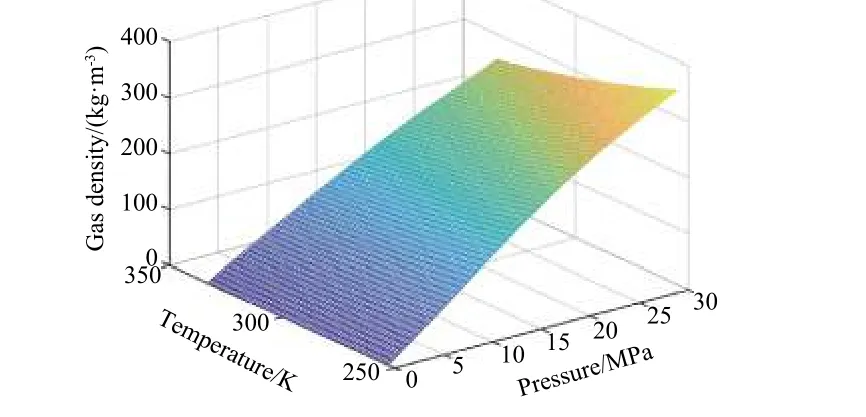
图2 NIST 数据库中的氮气密度-压力-温度关系曲面(253~333 K, 0~30 MPa)Fig. 2 Density-pressure-temperature profile of nitrogen(data from NIST database: 253~333 K, 0~30 MPa)
然而当需要快速求解气体密度,例如在对卫星在轨遥测数据进行实时判读期间,往往需要有气体密度与温度和压力的显式函数,以快速准确确定气体剩余量。鉴于此,本文依据NIST 物质物性平台,查询氮气密度随压力和温度变化的数据,采用双变量多项式、利用数据处理软件进行拟合,得到氮气密度与温度和压力的显式关系式。该拟合公式为5 次多项式,

其对应的多项式系数见表1,多项式拟合的均方根误差(RSME)为0.037 29。

表1 氮气密度-温度-压力关系式系数Table 1 Coefficients of density-temperature-pressure fitting expression for nitrogen
图3 和图4 给出理想气体状态方程和3 种真实气体状态方程在常温(293 K)、0~70 MPa 压力下和高压(30 MPa)、200~500 K 温度下的氮气密度计算结果,同时给出基于NIST 的显式算法得到的结果(图中以NIST 标注)作为对比。可以看到,3 种真实气体状态方程中,RK 方程对氮气密度的计算结果与NIST 结果最为接近。
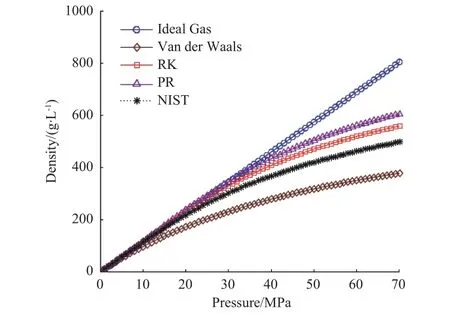
图3 不同计算模型的氮气密度计算结果比较(293 K、0~70 MPa)Fig. 3 Comparison among calculated results of nitrogen density by using different gas equations of state(293 K, 0 to 70 MPa)
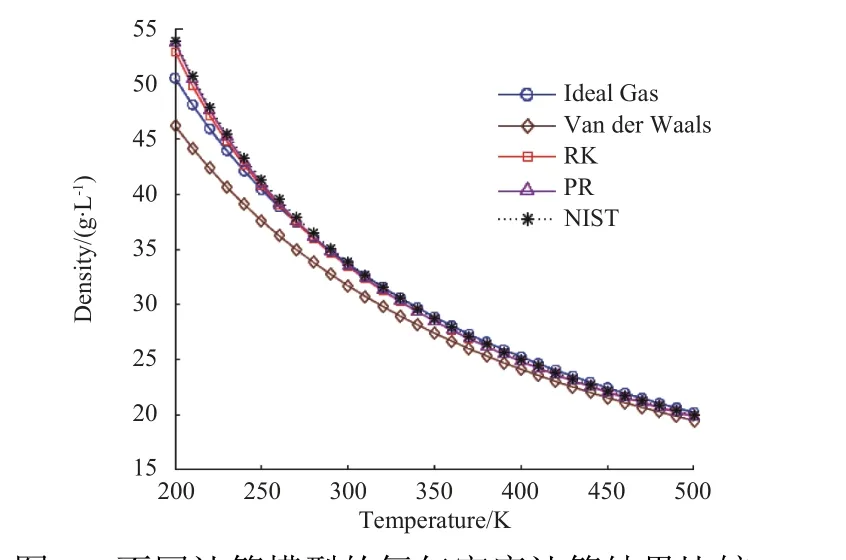
图4 不同计算模型的氮气密度计算结果比较(30 MPa、200~500 K)Fig. 4 Comparison among calculated results of nitrogen density by using different gas equations of state(30 MPa, 200 to 500 K)
1.3 气瓶容积修正方法
气瓶在充入高压气体后,其容积会有一定的膨胀。在实际工程应用中,会对气瓶在最大工作压力点的容积进行测量。假设容积变形量与压力呈线性关系,则有

式中:Pmax为最高工作压力,Pa;Vmax为最高压力下的气瓶容积,m3;P0为大气压力,Pa;V0为大气压力下的气瓶容积,m3。
综上,冷气推进系统工质剩余量计算公式可总结为
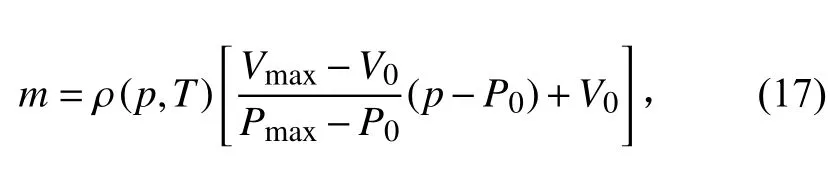
式中的气体密度需根据气体状态方程迭代求解或者根据本文显式计算方法得到。
2 地面加注测量结果与计算结果的比较分析
选取某批次48 L 复合材料气瓶产品的质心测量试验结果对氮气质量计算方法进行验证。该气瓶为薄壁金属钛内衬碳纤维缠绕的复合材料球形高压气瓶,额定初始工作压力30 MPa,在轨应用期间工质剩余量的计算精度要求优于0.3 kg,本批次共2 件产品。气瓶的质心测量试验在全自动高精度质心测量台上进行[14],如图5 所示,气瓶通过两端固定安装在质心测量台上——一端为固定出口端,一端为活动圆柱端。气瓶的出口端固定不动、而圆柱端可沿轴向伸缩,因此充气加压后,气瓶主要向圆柱端膨胀,径向膨胀量均匀且为相对小量,轴向膨胀伸长量可由预先安装的激光位移计测得。质心测量台具备实时称重功能,可直接获得工质的质量。

图5 气瓶质量与质心测量装置Fig. 5 Experiment setup of the tank mass and mass center measurement device
2.1 气瓶容积变化实测结果
利用质心测量台的位移测试功能,分别测量了不同压力下气瓶的轴向膨胀伸长量,结果如图6 所示。可以看到,轴向膨胀伸长量与气瓶压力呈线性关系,拟合决定系数(R2)分别为0.972 36 和0.996 51,线性度良好。这一结果也从侧面证明1.3 节中气瓶容积变形量与压力呈线性关系的假设成立。
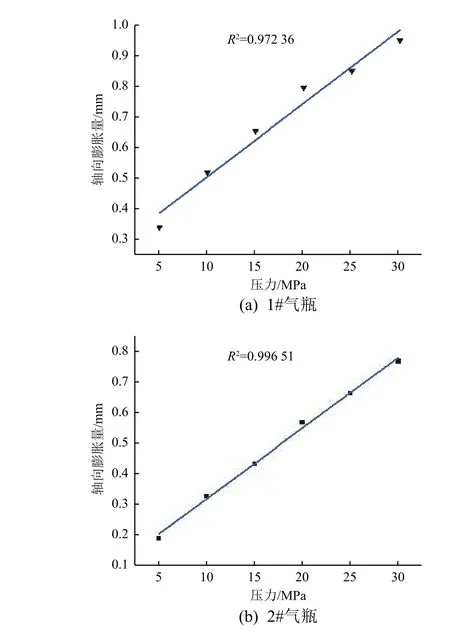
图6 气瓶轴向膨胀伸长量的测量结果Fig. 6 Measured axial deformation length of test tanks
气瓶的容积变形测量结果如表2 所示,其中V0和V30分别为大气压力和30 MPa 压力下的气瓶容积。
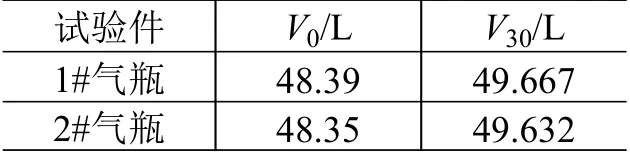
表2 气瓶容积变形测量结果Table 2 Measured results of tank volume under differentpressures
2.2 工质剩余量的实测结果
利用质心测量台的称重功能,分别测量了不同压力下气瓶内的气体质量,并与工质剩余量计算结果进行对比。表3 为不同计算方程的氮气剩余量计算结果相对于实测值的平均误差。可以看到,基于NIST 的显式算法平均误差最小,不超过0.05 kg;其次为RK 方程,而Van der Waals 方程的计算结果偏差最大。

表3 不同计算方程的氮气剩余量计算结果的平均误差(含容积修正)Table 3 Mean error of nitrogen residual mass values calculated by using different models
图7 给出2 件气瓶加注氮气质量试验的实测结果与不同计算方程的计算结果对比。从图中可以看出,基于NIST 的显式算法所得结果在数据绝对值和变化趋势上都与地面实测结果最为接近。

图7 气瓶加注氮气质量的实测结果与不同计算方程的计算结果(含容积修正)对比Fig. 7 Comparison between experimental fuel mass values and calculated results with volume correction
表4 对比分析了容积修正对基于NIST 的显式算法计算结果的相对误差影响。可以看到,容积修正能够有效减小气瓶内氮气剩余量计算结果的误差,并且压力越高,容积修正的效果越明显。

表4 容积修正对基于NIST 的显式算法计算结果的影响Table 4 Comparison between calculated nitrogen mass errors for NIST models with and without volume correction
2.3 工质剩余量计算误差分析
如前所述,卫星冷气推进系统工质剩余量计算需依据3 个输入条件——气瓶压力、气瓶温度和气瓶容积。设气瓶压力的不确定度为u(p)、气瓶温度的不确定度为u(T)、气瓶容积的不确定度为u(V),则有工质剩余量计算的相对不确定度u(m)[15]为
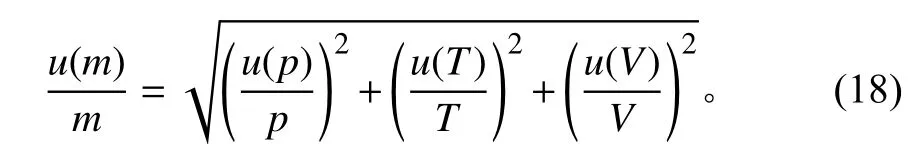
某卫星冷气推进系统配置了2 件48 L 气瓶,加注目标压力为30 MPa(20 ℃)。星上压力传感器采集压力值的不确定度u(p)为0.175 MPa,气瓶温度测量的不确定度u(T)为0.5 ℃,气瓶容积测量的不确定度u(V)为0.1 L,根据公式(18),该卫星工质剩余量计算的不确定度为0.18 kg,相对不确定度为0.62%。
3 结束语
本文提出一种卫星推进系统气体工质剩余量的显式计算方法,基于NIST 物质物性平台,给出氮气密度-温度-压力的显式拟合公式;并采用容积线性修正模型减小气体工质剩余量计算的平均误差。用地面加注量试验数据对计算模型进行验证,计算结果与测量结果间的误差总体上不超过0.05 kg,计算方法的不确定度为0.18 kg,满足工质剩余量的计算精度优于0.3 kg 的要求。
